山地框架剪力墙结构抗倾覆计算方法研究
张雪洁 崔英豪 胡其志
(武昌工学院 武汉430065)
引言
当房屋基础由于水平作用突然发生移动,上部由于惯性维持原来位置不变,导致建筑物沿高度分布水平力。林同炎[1]提出为保持平衡,必然会在基础产生相反水平力,由此形成倾覆弯矩(M=Ha)。倾覆弯矩计算方法非常重要,影响结构设计参数选取及结构布置[2,3]。目前关于倾覆弯矩的规范要求均是针对普通结构,掉层结构由于不等高接地,受力特点异于常规结构[4],其倾覆问题成为山地结构研究体系必不可少的内容。此外,掉层结构研究多集中在框架结构[5],关于框剪结构研究较少。本文首先分析山地掉层结构倾覆稳定的特殊性,进而讨论规范方法与力学方法计算山地框剪结构倾覆弯矩的利弊,根据结果提出建议。
1 掉层结构抗倾覆问题
计算倾覆弯矩前提是确定倾覆点,赵耀[6]认为掉层结构在正向倾覆荷载作用下,下接地部位为计算倾覆点,在负向倾覆荷载作用下,上接地部位为计算倾覆点。当结构受正向倾覆荷载时,由于上接地有上抬趋势,下接地侧结构对土体有受压趋势,受压点必然在下接地侧某点,同样结构受负向倾覆荷载作用时,下接地侧有上抬趋势,上接地侧对土体有受压趋势,结构与地基接地点必然在上接地部分中某点,为方便计算,将倾覆点分别取为各自端点,如图1a中的下接地侧A点与图1b中上接地侧B点。
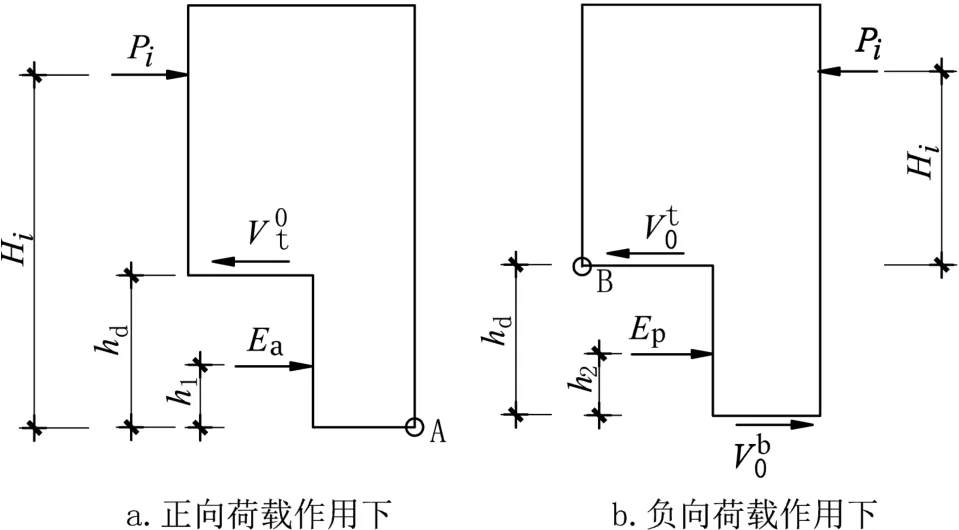
图1 荷载作用下结构受力Fig.1 Structural illustration under force
1.1 掉层结构倾覆弯矩
结构正负向倾覆弯矩表达式:

式中:M0v为结构整体倾覆弯矩;Pi为水平侧向力;Hi为水平侧向力与计算倾覆点的距离;Ea为掉层结构掉层部分楼层承受的主动土压力;Ep为掉层结构掉层部分楼层承受的被动土压力;h1为主动土压力合力点到下接地面的垂直距离;h2为被动土压力合力点到下接地面的垂直距离;hd为掉层结构掉层部分高度;Vt0、Vb0为上、下接地部分剪力。
不考虑土压力,结构在单个正负向相同荷载作用下,由式(3)可得正负向倾覆弯矩相同。当多个外荷载作用时,由力的叠加原理仍可得相同结果。
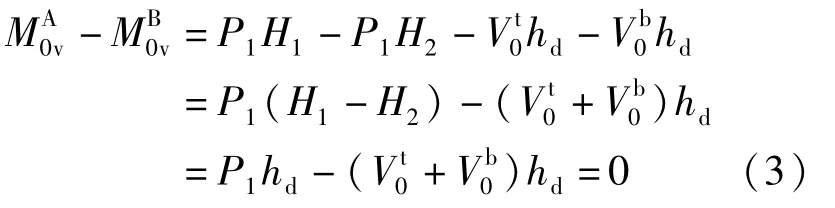
考虑土压力,由式(4)可知,主动土压力Ea小于被动土压力Ep,主动土压力作用点距下接地距离h1和被动土压力作用点距下接地距离h2小于掉层高度hd的一半,即h1<hd/2,hd-h2>hd/2,因此正向倾覆弯矩小于负向倾覆弯矩。
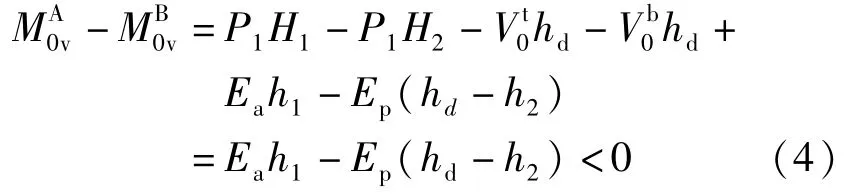
1.2 掉层结构抗倾覆弯矩
对于普通结构,正负向抗倾覆弯矩相等,掉层结构由于有两个不同的接地端,其抗倾覆弯矩计算与普通结构不同。图2为掉层结构计算简图。
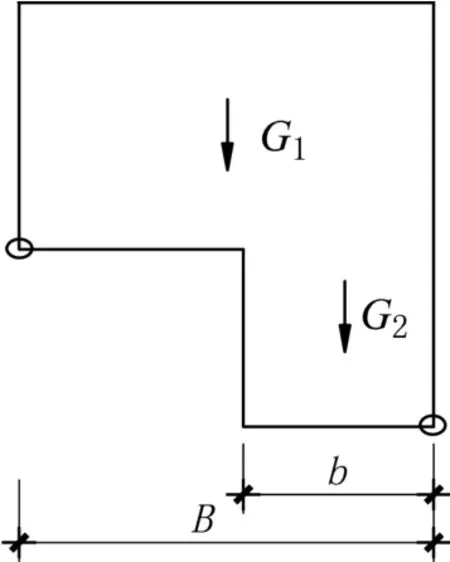
图2 抗倾覆弯矩计算示意Fig.2 Resist overturning moment calculation diagram
正向荷载作用,倾覆点在下接地层外侧,抗倾覆弯矩为:
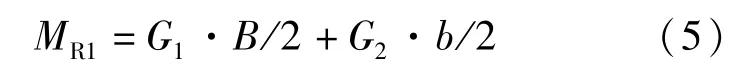
负向荷载作用,倾覆点在上接地面外侧,抗倾覆弯矩为:
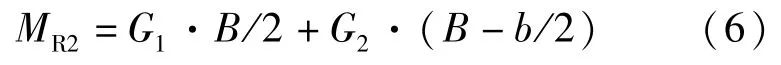
则不同倾覆点的抗倾覆弯矩之差为:

由式(7)可知,正负向荷载作用下,掉层结构抗倾覆弯矩不相同,正向抗倾覆弯矩小于负向抗倾覆弯矩,而掉层结构在不考虑土压力时正负向倾覆弯矩相等,考虑土压力时,正向倾覆弯矩小于负向倾覆弯矩。因此,对于掉层结构,在正向倾覆荷载作用下,结构处于更加危险的状态,结构以正向倾覆荷载下抗倾覆计算为准。
2 山地框剪结构倾覆弯矩计算方法
已知明确的外力施加在结构上,结构倾覆弯矩可由外力容易求得,而实际多数情况下,只能求得外荷载作用在结构上产生的内力,若将内力换算为荷载不仅繁琐,而且也难以确定荷载模式,这种方法不可取,所以倾覆弯矩一般以结构内力形式表达。
2.1 抗规方法计算
《建筑抗震设计规范》(GB 50011-2010)中6.1.3条指出框架抗震墙结构中框架结构承受的地震倾覆力矩可按:
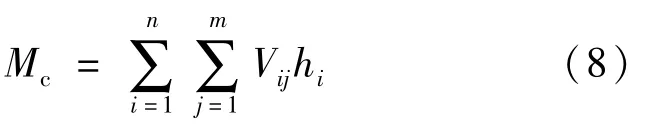
规范方法是简化方法,倾覆弯矩由内力值表达,其普遍适用于常规结构。掉层结构由于自身特殊性,需建立模型对式(8)加以推导。若将地震力等效为静力作用于每个楼层上,则每个楼层都将受到集中荷载作用。建立一掉4层3跨模型,计算简图如图3所示,①、②等表示杆件编号,P1、P2、P3、P4表示从上到下作用在楼层上的集中力,Vij表示第j个作用力在第i个杆件产生的剪力。

图3 抗规方法计算简图Fig.3 Seismic code method calculation model diagram
P1、P2、P3、P4单独作用时,杆件内力关系见式(9)~式(12):
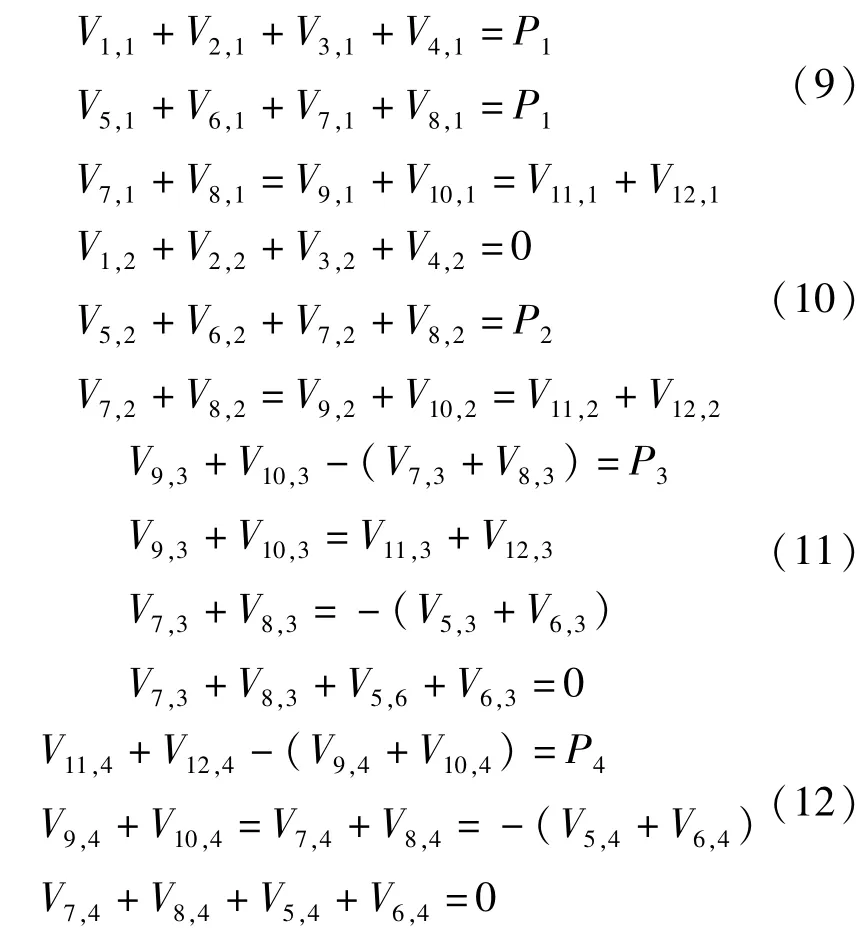
可得各集中力与杆件剪力的关系如下:
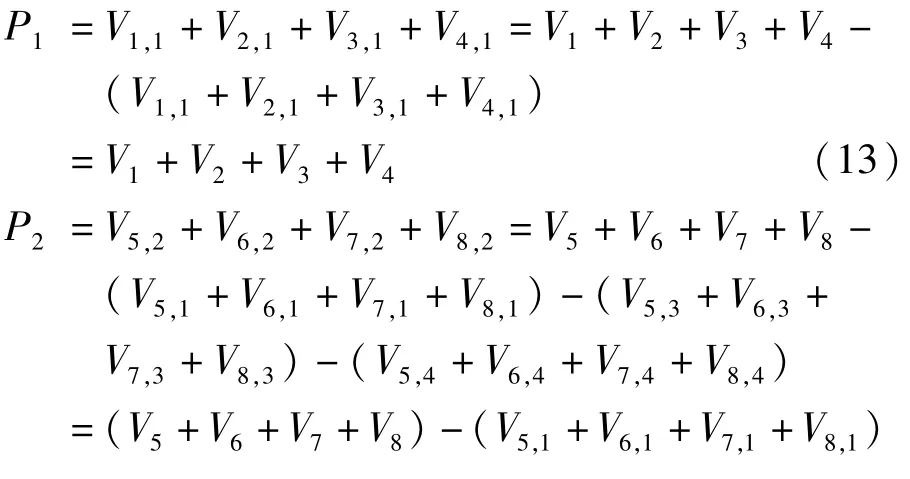
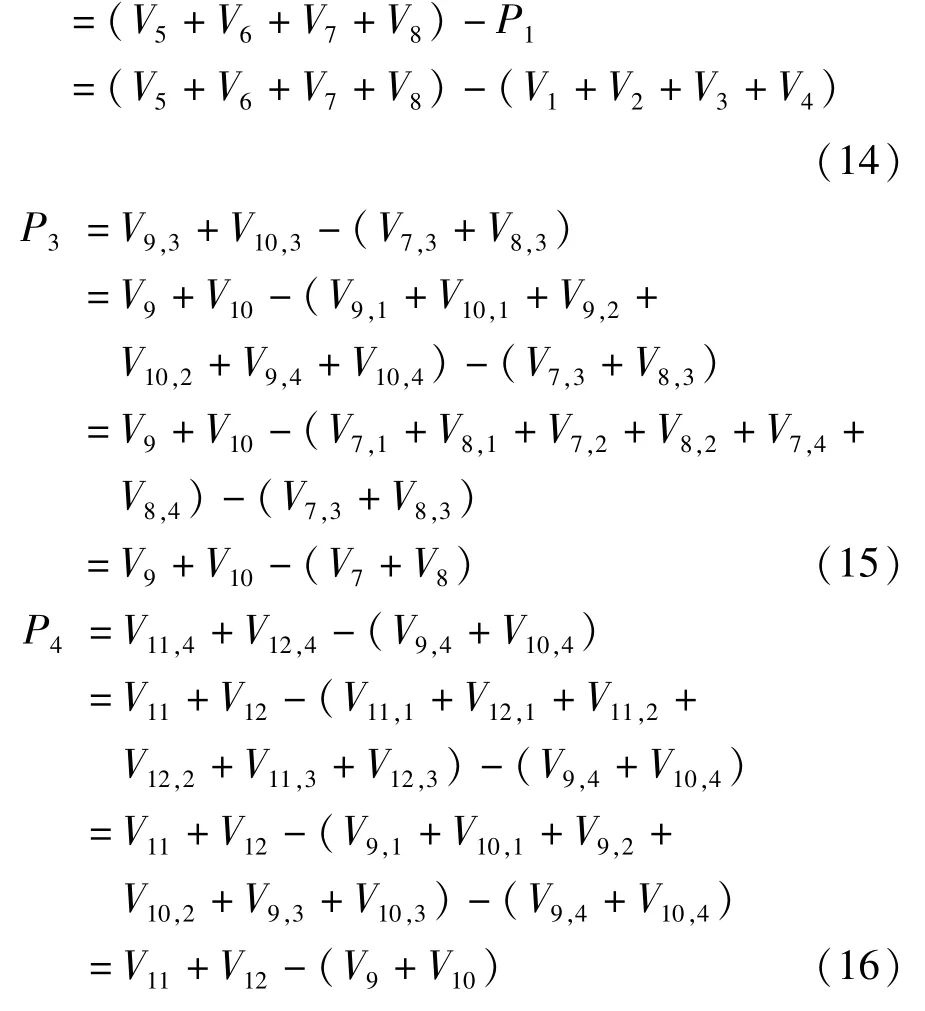
结构倾覆弯矩可表示为:

由以上推导可知,掉层结构可采用抗规计算方法,即将各层剪力与层高的乘积累加作为掉层结构倾覆力矩。
2.2 力学方法计算
关于倾覆弯矩计算方法,除了规范方法,还有按柱底轴力计算的方法,需要先确定底部各杆件轴力的合力作用点。计算方法为:

其中:x0为x向合力作用点;Ni为x向规定水平力下各构件轴力;xi为墙柱或柱x向中心点坐标。
则框架柱和墙承担的倾覆力矩为:
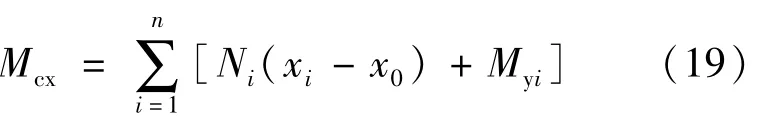
框剪结构看作整体,基底任意位置作为取矩点,式(19)计算的倾覆弯矩必为定值,即为外力合力矩。山地框剪结构有两个不同接地端,采用式(19)计算倾覆弯矩时,将其视为整体,取接地构件轴力和弯矩进行计算。
2.3 算例分析
对比规范方法与力学方法对计算山地框剪结构倾覆弯矩的差异,建立如图4所示模型,其中剪力墙长均为3m,共D-5-4、D-3-3、D-1-2三个模型,取C轴进行研究,部分立面图见图5a为掉一层一跨,用D-1-1表示,图5b掉五层四跨,用D-5-4表示。模型跨度6m,层高3.6m,框架墙、柱混凝土C40,梁混凝土C30,钢筋HRB400,楼板厚度100mm,梁截面250mm×500mm,柱截面600mm×600mm,剪力墙厚度为250mm,总层数为15层,纵向6跨,横向4跨。
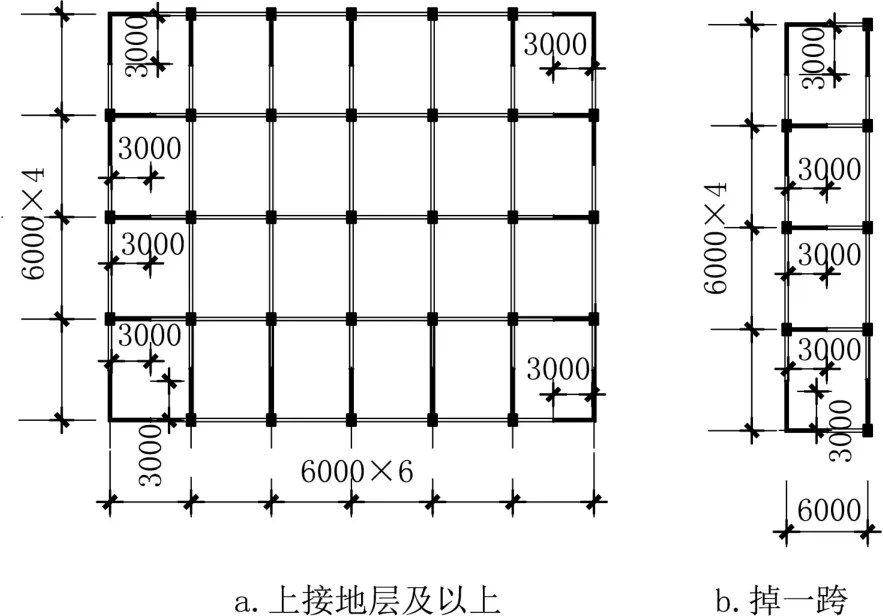
图4 结构布置平面示意Fig.4 Structure layout plan

图5 C轴部分模型立面示意Fig.5 Elevation drawing for axis C
在各节点分别施加逐层增大50kN倒三角荷载,100kN均布荷载以及顶层节点1000kN集中荷载,结果见表1~表3,限于篇幅,表2和表3只给出最终结果。可以看出,力学方法计算结果比抗规方法略大,但二者误差均未超过1%,可认为两种计算方法结果基本相同。同时也说明抗规方法虽是简化方法,但结构作为整体来计算基底倾覆弯矩时能取得满意精度。
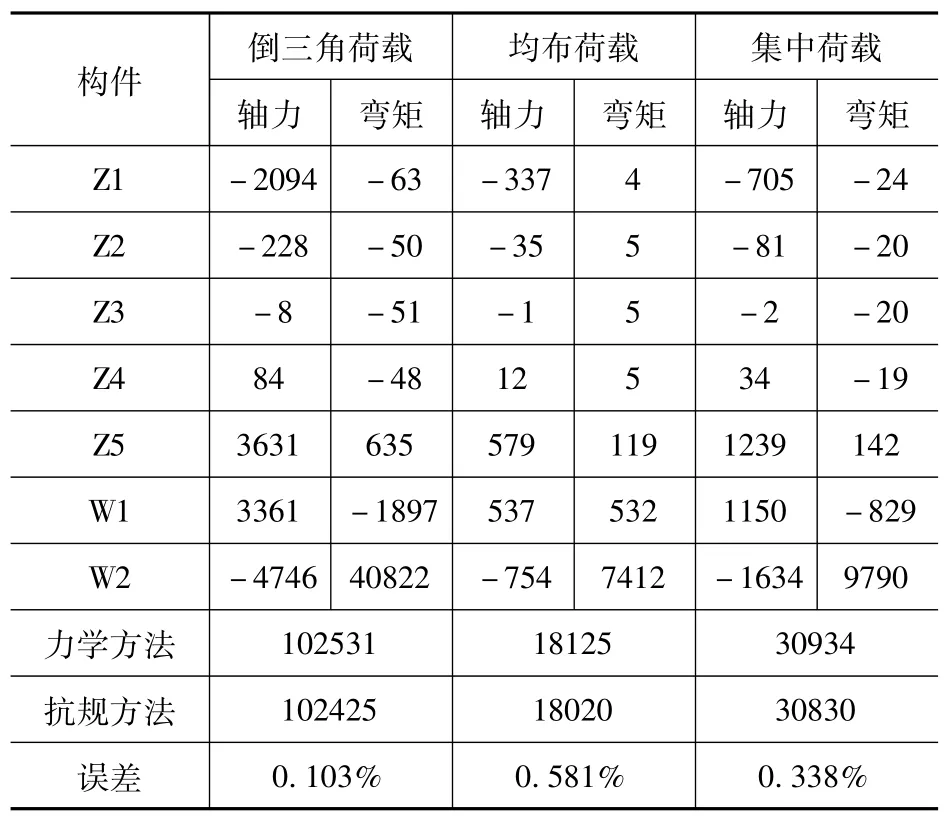
表1 D-5-4构件轴力及弯矩(单位:kN)Tab.1 Axial force and bending moment of D-5-4 (unit:kN)

表2 D-3-3倾覆弯矩(单位:kN)Tab.2 Axial force and bending moment of D-3-3(unit:kN)
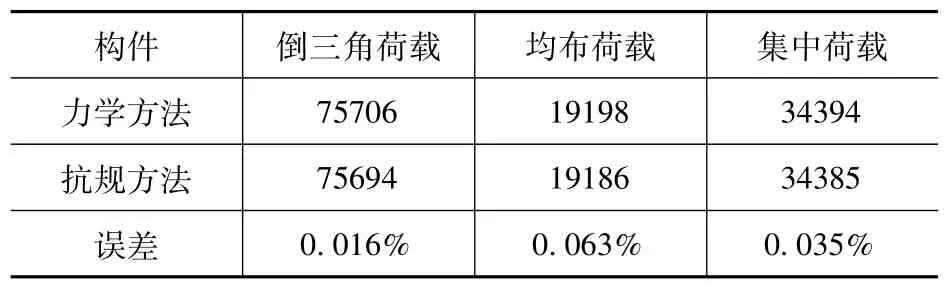
表3 D-1-2倾覆弯矩(单位:kN)Tab.3 Axial force and bending moment of D-1-2(unit:kN)
对于框剪结构,底层框架承担倾覆力矩计算的准确性将对结构设计参数选取有较大影响,在普通框剪结构中,已有研究表明力学方法计算框架承担倾覆力矩比例大于抗规方法计算结果,因此对于山地框剪结构需考虑这一问题。表4即为三种不同荷载模式下两种方法计算的结果,其中抗规方法结果为上接地层框架柱承担的倾覆弯矩占本层倾覆弯矩的比例。对于山地框剪结构,框架承担的倾覆弯矩比例和普通框剪类似,均是力学方法计算结果大于抗规方法,但随着掉层掉跨数增大,两者差距出现减小趋势。
从方法上讲,力学方法以接地端构件的轴力和弯矩来进行计算,更加符合倾覆弯矩概念,但是对于合力点选取需进一步探究,合力点计算位置不同,框架承担的比例也会不同。我国抗规方法已沿用多年,且根据框架承受倾覆弯矩比例不同所采取的各种措施也是基于抗规方法确定的,但抗规方法是简化方法,忽略墙与楼板/梁的交接处存在较大弯矩的事实,低估了框架承担的倾覆力矩。两种方法各有利弊,设计人员应根据实际结构合理选择。

表4 不同方法计算框架承担倾覆弯矩比例Tab.4 Overturning moment ratio by frame with different methods
3 剪力计算方法
抗规方法目前仍是设计人员计算结构倾覆弯矩最常用的方法。我国规范采用振型分解反应谱法对结构倾覆弯矩进行计算,这必然涉及到剪力的计算问题。剪力计算方法的准确性对倾覆弯矩计算有较大影响。
3.1 常规结构剪力计算方法
规范规定倾覆力矩计算采用规定水平力。关于规定水平力,我国规范中多处均有涉及,主要体现在抗规6.1.3条、高规8.1.3条。但对于框架剪力墙结构,规定水平力如何计算一直以来是众多学者讨论的热点。由于振型分解反应谱法是采用各振型组合后的结果,因此组合的先后顺序将会导致计算结果不同。剪力计算如式(20)、式(21)所示:
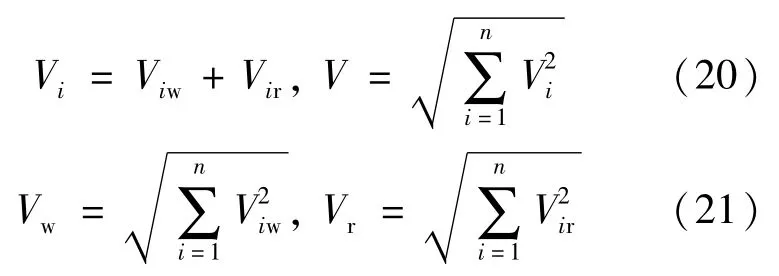
式中:Vi表示第i阶振型的层剪力;V为结构的层剪力;Viw、Vir分别为第i阶振型剪力墙和框架的剪力;Vw、Vr分别为振型组合后的剪力墙剪力和框架剪力。
由基本的数学知识可知,V≤Vw+Vr,即框剪结构层剪力小于相应楼层剪力墙和框架的剪力之和。式(20)表示振型组合之后的层间剪力,称为组合剪力,而将式(21)两式之和称为求和剪力。
3.2 山地框剪结构剪力计算方法
选取普通10层、15层框剪结构,以及2.3节中掉五层四跨框剪模型D-5-4。采取振型分解反应谱法,对比采用组合剪力、求和剪力计算的差异,计算结果见表5。
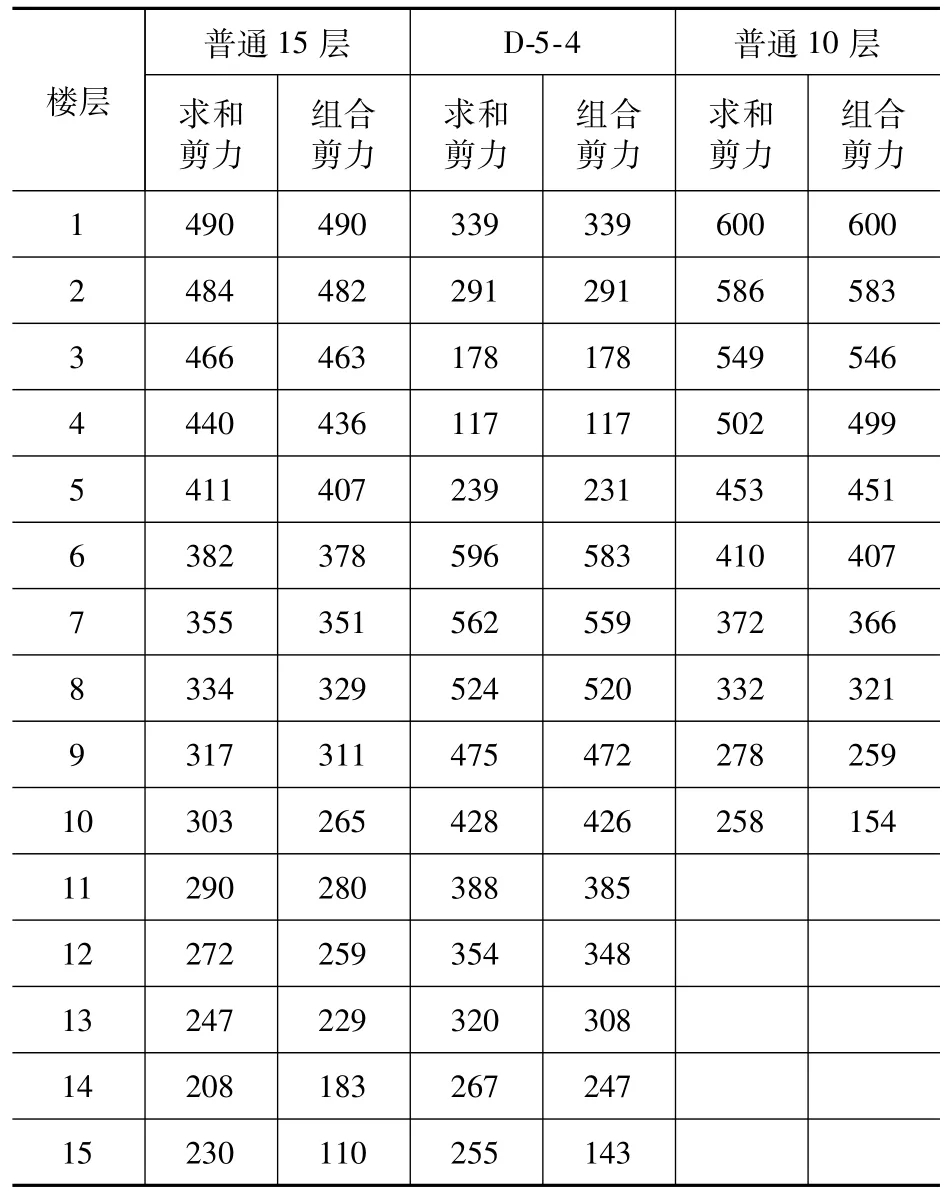
表5 剪力计算方法对比(单位:kN)Tab.5 Comparison of shear calculation method (unit:kN)
由表5可知,在结构底部,二者计算出层间剪力差别不大,在结构上部尤其是结构顶层,二者计算出剪力差别较大。这是因为对于框剪结构,在顶部会出现剪力墙位移相对较大的情况,随着剪力墙和框架协调变形,会使框架受到反向作用力,与框架原有作用力叠加后会使剪力减小甚至为负值,此时按照式(20)相加之后,再进行振型的组合后会使层剪力减小。而按照式(21)计算,先进行振型组合,此时负值剪力经平方和开方后已变为正值。因此,除了计算方法本身原因,还要加上结构顶部框架负向剪力组合顺序问题,使得在顶层两种方法计算结果差距较大。
求和剪力大于组合剪力,则由求和剪力计算的倾覆弯矩必然会大于组合剪力计算的倾覆弯矩,而且剪力差距经与层高乘积累加之后这种差距会增大,因此当结构层高越大时,这种差距会越明显。为验证这一结论,图6给出了求和剪力与组合剪力求得的各层倾覆弯矩之差。
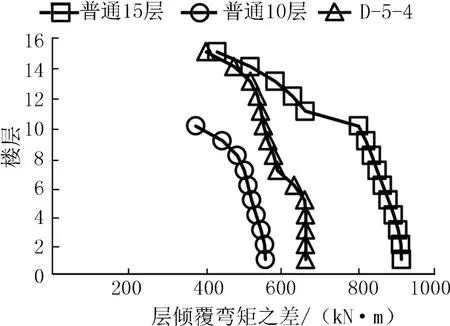
图6 两种方法层倾覆弯矩之差Fig.6 Difference value between layer overturing moment by two methods
从图6中可以看出,两种方法计算的倾覆弯矩差异较明显,而且这只是对结构中某一轴线进行分析,对于比较复杂的大型结构,随着构件增多,两种方法计算的倾覆弯矩必然差距更大,使用求和剪力偏安全,因此建议采用求和剪力来计算山地框架剪力墙结构的倾覆力矩。
4 结论
1.在不同方向倾覆荷载作用下,掉层结构倾覆计算点也不相同,不考虑土压力时,正负向倾覆弯矩相同;考虑土压力时,正向倾覆弯矩小于负向倾覆弯矩。
2.普通结构正负向抗倾覆弯矩相同,而掉层结构正向抗倾覆弯矩小于负向抗倾覆弯矩,抗倾覆弯矩的计算以正向为准,也就是以下接地外侧的抗倾覆弯矩为准。
3.当结构作为整体来计算基底倾覆力矩时,采用规范方法计算可行,但规范方法忽略了楼板/梁的交接处弯矩,低估了底层框架承担的倾覆弯矩。
4.采取抗规方法计算倾覆弯矩涉及到剪力计算,对比了组合剪力与求和剪力计算结果,建议采用求和剪力来计算山地框剪结构的倾覆弯矩。

