整体倾斜下砌体结构房屋安全性能研究*

章晓咏赵德波何鹏

（1.重庆大学山地城镇建设与新技术教育部重点实验室 400045；2.重庆大学土木工程学院 400045；3.重庆永渝检验检测技术有限公司 400061）

引言

砌体结构在我国使用范围广泛、历史悠久，21世纪前建造的房屋大部分为砌体结构或砖木、砖混合结构。由于经济、技术、管理等水平相对落后，现存的大批砌体结构房屋中，不少房屋存在质量缺陷，甚至安全隐患。其中，由于地基选择或处理不当，后期地基不均匀沉降引起结构的整体倾斜就是一个突出问题［1］。

文献［2］等研究了在地基不均匀沉降时，上部结构的振型、变形和内力等相关参数的分析，该类研究多集中于框架结构；Skempton和Mac-Donald［3］通过对98栋倾斜建筑进行统计调查，建议以0.002作为建筑物的允许角变量；Grant［4］等在Skempton研究的基础上，提出以0.003作为建筑物出现裂缝的极限角变量；Boscardin和Cording［5］为研究水平应变对砌体结构的影响，把结构简化为一根简支梁，给出角变量的计算公式。

由于基础不均匀沉降导致砌体结构倾斜甚至倒塌在工程中并不罕见，钟万善［6］对甘肃省酒泉市地区7个县（市）33栋有裂缝的建筑物进行了调查分析，其中17栋是因地基不均匀变形（沉降）造成的，占调查栋数的51.5%。

当砌体结构房屋在软弱地基上采用筏基或刚度较大的条形基础时，由于基础整体刚度大，当发生不均匀沉降时，沉降模式接近直线形沉降，房屋往往表现为整体倾斜。在工程中发现，部分基础整体性较好的砌体结构房屋，倾斜角度超出相关规范限值时（我国规范及有关学者们提出的建筑物允许角变量限值见表1），上部结构却未出现结构性裂缝或很少，但其结构安全性多被判定为Cu级或Du级，造成较大的浪费。因此，研究整体倾斜对砌体房屋结构安全性能的影响，具有重要的社会意义和工程应用价值。

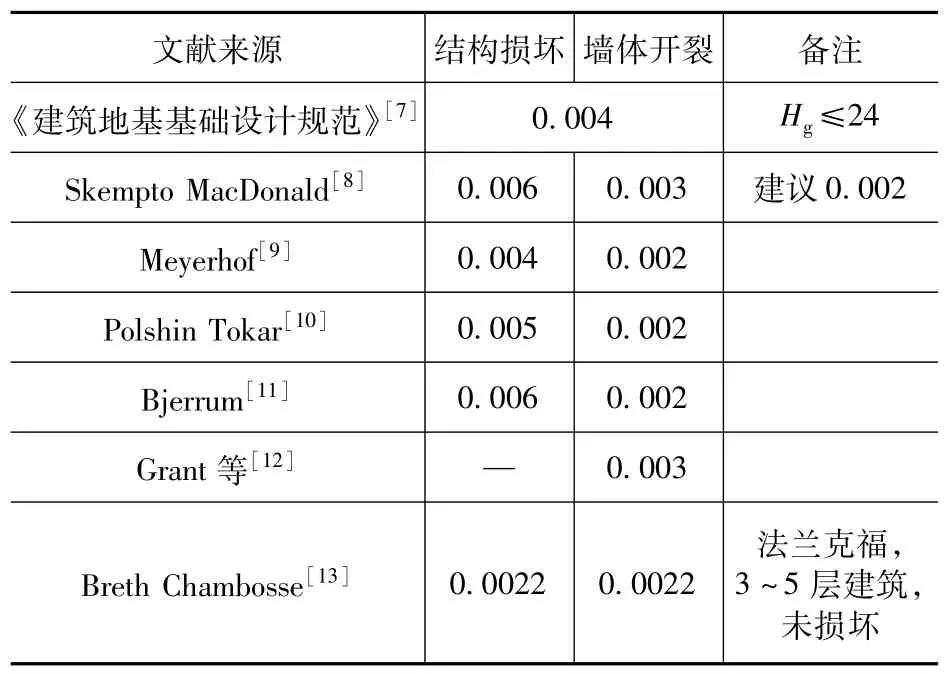
表1 建筑物允许角变量Tab.1 The limiting angle of buildings

1 模型设计和软件选用

1.1 模型设计

多层砌体结构在整体倾斜下，影响其安全性能的因素很多，本文选用整体倾斜角度（结构顶部位移与结构高度的比值，下同）、层数、开间大小和洞口尺寸等作为关键影响因素。并以此为依据设计了96个纵横墙混合承重的模型。将96个模型分为12组，每一组内各有8个模型，其倾斜角度分别为0、2‰、3‰、4‰、5‰、6‰、10‰和20‰，分组详情见表2。算例设计中，板厚100mm，为C30混凝土；墙厚240mm，砌体弹性模量E=2400MPa，泊松比μ=0.15，重量密度18kN/m3。所有算例的底层高4.2m，其他楼层的层高3m，算例示意见图1。

表2 模型分组Tab.2 The detail of each group

运用有限元软件SAP2000对结构进行内力分析，采用壳单元模拟墙体、楼板，对壳单元进行网格划分，最大长度1200mm，楼板指定自动边束缚。墙底部布置地梁，用杆单元模拟地梁，并放大梁的抗弯刚度为无穷大，以模拟刚性地基。在附加坐标系中建立模型，通过旋转附加坐标系的角度，以模拟结构的整体倾斜程度。通过截面切割功能可以计算出墙肢在倾斜前后的轴力、弯矩。楼（屋）面附加恒载取1.5kN/m2，活荷载取2kN/m2。

图1 算例示意Fig.1 The numerical example schematic diagram

1.2 软件选用

砌体是砌块和砂浆的组合结构，有限元分析时可以采用两种方式进行建模。其一是分离式模型，砌体和砂浆分别建模，这种方式更能反应结构的破坏机理，但是模型复杂，适用于模拟小型砌体结构或构件，尤其是模拟试验；其二是整体连续模型，连续材料的相关参数可以通过实验获得，或者采用规范数据，适合于整体结构的工程应用分析。昆明理工大学刘振宇等［14］把砌体结构等效为均质材料，并与意大利学者Galiv做的一片足尺砌体结构的剪压实验进行对比，结果吻合良好，证明了整体连续模型的合理性。本文属工程应用研究，算例为仅考虑竖向荷载作用下的整体倾斜分析，主要受力构件均为竖向受压构件。因此，在计算中采用各向同性材料整体连续模型来模拟，材料参数参考我国规范砌体受压构件计算参数取值，可认为能够满足本文研究需要，且已较目前砌体结构工程设计通用软件更为精细化。

采用结构有限元软件SAP2000对96个模型进行弹性计算分析，以板壳单元模拟墙；用杆单元模拟地梁（地梁代表基础），并修正杆的刚度为无限大，以模拟刚性基础。在附加坐标系下建模，通过转动附加坐标系的转角，以模拟结构的整体倾斜，并规定倾斜方向为由D轴→A轴方向转动。本文选取的模型为对称结构，故重点分析A、B、C、D轴上1-2轴、2-3轴和3-4轴区间的墙体，每一层选取3个控制截面，分别为底部、中部和顶部控制截面。选取以下参数进行分析：

根据式（1）进行承载能力验算：

其中：γ0为结构重要性系数，取1.0；S为荷载效应组合的设计值，本文为轴力N，由软件计算确定；R为结构构件抗力的设计值，本文为按规范公式计算出的极限承载力Nu。

Nu依据砌体结构设计规范［15］，按式（2）计算：

其中：Nu为墙肢极限承载力设计值；φ为墙肢高厚比和轴向力的偏心距对墙肢的承载力影响系数；f为墙肢抗压强度设计值；A为墙肢横截面积。

取R0、S0分别为未倾斜的抗力和效应设计值；R1、S1分别为倾斜后的抗力和效应计算值。以抗力效应比（R1/S1）/（R0/S0）的最小值（下文简称（R1/S1）/（R0/S0）），即（N1/Nu1）/（N0/Nu0），来表示结构的安全性的变化。其中：N1为倾斜后的墙肢轴力；Nu1为倾斜后的墙肢极限承载力设计值；N0为倾斜前的墙肢轴力；Nu0为倾斜前的墙肢极限承载力设计值。

2 计算结果及分析

假设结构在未倾斜时的抗力效应比为1，即倾斜前原结构安全性能刚好满足规范要求。通过计算，结构倾斜后与倾斜前的抗力效应比值（R1/S1）/（R0/S0）见表3，倾斜角度与（R1/S1）/（R0/S0）的关系见图2。

表3 不同倾斜角度下（R1/S1）/（R0/S0）最小值汇总Tab.3 Sum of minimum value （R1/S1）/（R0/S0）under different tilt angle

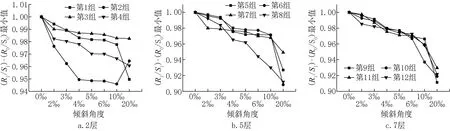
图2 不同倾斜角度下（R1/S1）/（R0/S0）最小值Fig.2 The minimum value （R1/S1）/（R0/S0）under different tilt angle

根据表3与图2可知：

（1）倾斜角对结构安全性能的影响：随着倾斜角度的增加，控制截面（R1/S1）/（R0/S0）逐渐减小。在倾斜角度小于6‰时，（R1/S1）/（R0/S0）降低幅度在5%以内；在倾斜角度小于10‰时，（R1/S1）/（R0/S0）变化范围在7%以内；在倾斜角小于20‰时，（R1/S1）/（R0/S0）变化范围在11‰以内。

（2）层数对结构安全性的影响：层数对（R1/S1）/（R0/S0）的影响无明显规律，在96个模型中，若只考虑层数变化，可分为32组模型，其中有29组模型的抗力效应比的变化范围在5.1%以内，最大变化为7.8%。

（3）洞口尺寸对结构安全性能的的影响：洞口尺寸对结构安全性能的影响无明显规律，在96个模型中可分为48组，每组模型内部的变量只有洞口尺寸，其中有47组模型的抗力效应比的变化范围在3.9%以内，最大变化为5.7%。

（4）开间尺寸对结构安全性的影响：开间尺寸对结构安全性的影响无明显规律。96个模型中，可以提取48个模型，分为24组，每组内部的变量只有开间尺寸，所有组的抗力效应比的变化范围均在3.5%以内。

3 整体倾斜角度限值

现将图2中96个模型的数据，汇总在图3中。

图3 不同倾斜角度下（R1/S1）/（R0/S0）最小值Fig.3 The minimum value （R1/S1）/（R0/S0）under different tilt angle

由图3可知，在倾斜角度小于6‰时，（R1/S1）/（R0/S0）最小值均大于0.95（图3 中虚线处（R1/S1）/（R0/S0）最小值为0.95）。根据《民用建筑可靠性鉴定标准》［16］第5.4.2条中对主要构件R/γ0S≥0.95 时评定为Bu级，（R1/S1）/（R0/S0）小于0.95时，构件评定为Cu或Du级，因此选取0.95作为一个评定指标。假设所有模型倾斜角度为0‰时，R/γ0S=1。当整体倾斜角度达到6‰作为参考。当倾斜角度到达20‰时，结构的抗力效应比降低11.8‰，在对砌体结构进行安全性的评定时，可以作为参考。

在实际工程中，如果结构在倾斜稳定后，其倾斜角度小于6‰，且未出现明显的结构性裂缝，此时可以不对结构采取处理措施。如果结构倾斜小于6‰，但出现较明显的结构性裂缝，考虑到设计、施工质量或其他不确定因素导致的安全隐患，应进一步检测鉴定（包括计算复核）后确定结构的安全性能。对于倾斜大于6‰的结构，不管其是否出现明显的结构性裂缝，也建议进一步检测鉴定（包括计算复核）后确定结构的安全性能。

4 结论

通过对整体倾斜下砌体结构在竖向荷载作用下的模拟计算分析，得出以下结论：

1.砌体结构整体倾斜时，倾角是影响其安全性能最主要的因素，随着倾斜角度的增加，倾斜前后房屋的抗力效应比（R1/S1）/（R0/S0）的最小值逐渐下降，安全性能下降。

2.当倾斜角度小于6‰时，在仅考虑竖向荷载时，倾角对结构的安全性能没有明显影响，倾斜后与倾斜前抗力效应比最小值大于95%。

3.在实际工程中，地基变形稳定后，对于倾斜角小于6‰，且未出现结构性裂缝的砌体结构，可不采取措施；若倾斜角度小于6‰且结构出现结构性裂缝，或者倾斜角度大于6‰，应进一步检测鉴定（包括计算复核）后确定结构的安全性能。