重庆某高层剪力墙结构住宅楼超限分析及优化设计*

刘鹏飞魏巍，2邱天

（1.重庆大学土木工程学院 400045；2.重庆大学山地城镇建设与新技术教育部重点实验室 400045）

引言

从20世纪初最早由日本提出简单的抗震设计思路，到目前普遍认可的“小震不坏，中震可修，大震不倒”的基本思想，结构抗震设计得到了长足的发展和进步，基于性能的结构抗震设计思想最早在20世纪70年代由新西兰学者Park所提出，并被认为是未来抗震设计的主要发展方向。其目的是在未来的抗震设计中，能有效地控制结构在不同水平地震作用下的破坏形态，实现不同的性能目标，并且使建筑物在整个使用过程中，在考虑各种可能遭受的地震作用下，总体花费也达到最小。1951年，Lin［1］利用结构刚心和质心的概念，第一次提出了刚心分析法，分析了平扭耦联对边缘柱、墙等抗侧力构件内力的影响。美国UBC-97和FEMA273、欧洲EC4都规定了扭转位移比的限值，其中美国规范不控制周期比，它对每层的扭矩作了放大，以考虑扭转不规则对构件内力的影响，强调结构的地震反应和构件的内力。日本的混凝土计算标准AIJ把偏心距和层刚度回转半径这两个参数作为控制扭转的限值。我国《高层建筑混凝土结构技术规程》（JGJ3-2010）［2］（以下简称《高规》）规定复杂高层建筑抗震设计时宜考虑平扭耦联对结构的扭转效应，振型数不应小于15，且计算振型数应使各振型参与质量之和不小于总质量的90%。我国规范把位移比大于1.2定义成平面不规则中的扭转不规则，本文参照美国规范，提出周期比不大于0.85～0.9的限值要求，强调结构的自振特性。重庆市抗震设防烈度虽仅为6度，但高层建筑密集，其中高层住宅的建造量很大，且常因功能需要，建筑平面与竖向布置复杂，出现了大量的“超限”高层，需进行抗震性能分析。尽管能够通过位移比、偏心率来判断结构的规则与否，但是多高层结构刚度中心的位置很难确定，而且不同的结构对位移比、偏心率的敏感度也不一样，目前来看此方法具有一定的合理性。

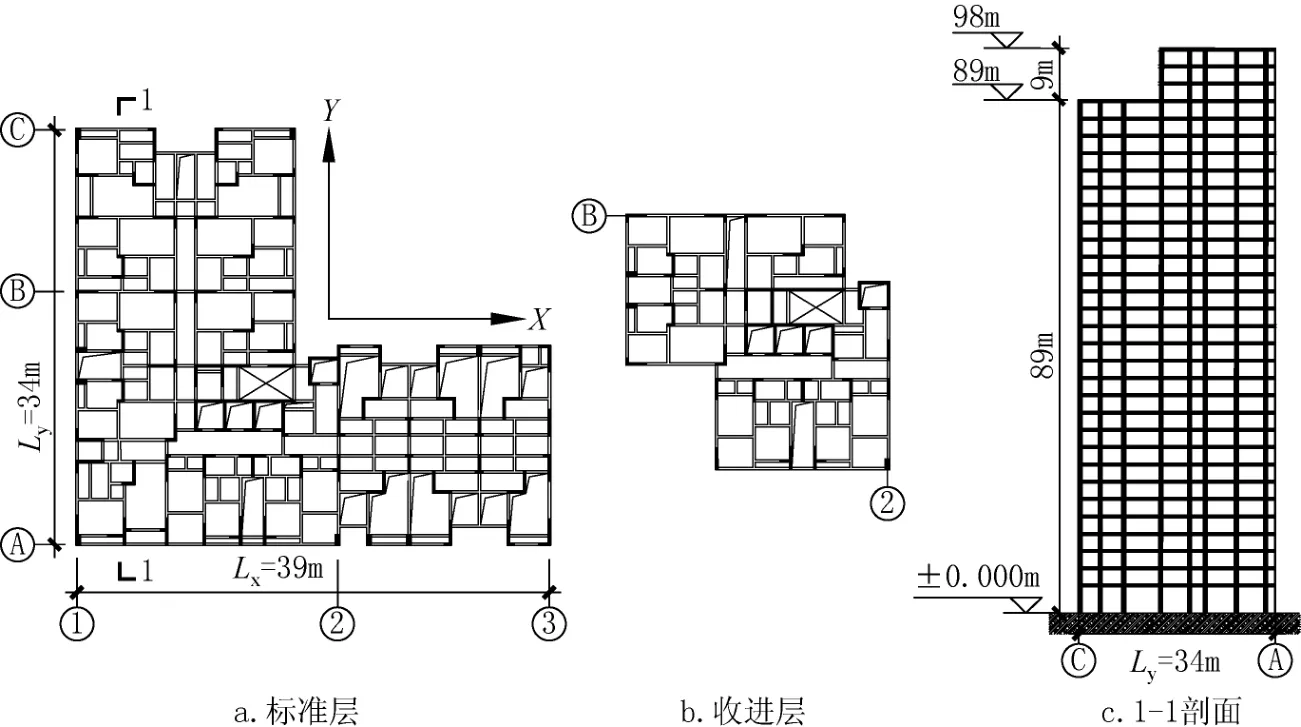
图1 结构平面布置图Fig.1 The even layer plan

1 工程概况

本项目位于重庆市主城区，工程地质情况良好；建筑平面布置为L型（无地下室，平面长度Lx=39m，宽度Ly=34m），采用剪力墙结构体系（见图1）；结构嵌固端位于桩基顶部，主体总高度98m，共32层；首层高度5m（墙肢厚度300mm），其余各层高度均为3m（墙肢厚度200mm），1～3层为剪力墙底部加强部位。建筑奇数层平面在L型②～③轴存在跃层情况，楼板开洞面积较大；结构在89m处存在上部楼层收进；墙、柱混凝土强度等级为C60（1层～3层）、C55（4层～7层）、C50（8层～15层）、C40（16层～24层）及C30（25层～屋顶），梁、板混凝土强度等级为C30，纵筋等级为HRB400，箍筋、墙分布筋等级为HPB300［3］。

2 结构超限判定及抗震性能目标设定

依据国家《超限高层建筑工程抗震设防专项审查技术要点》［4］（2015 年）及《重庆市超限高层建筑工程界定规定》［5］（2016 年）相关规定，结合结构平面、竖向布置与初步弹性分析，对结构做出超限判定见表1。

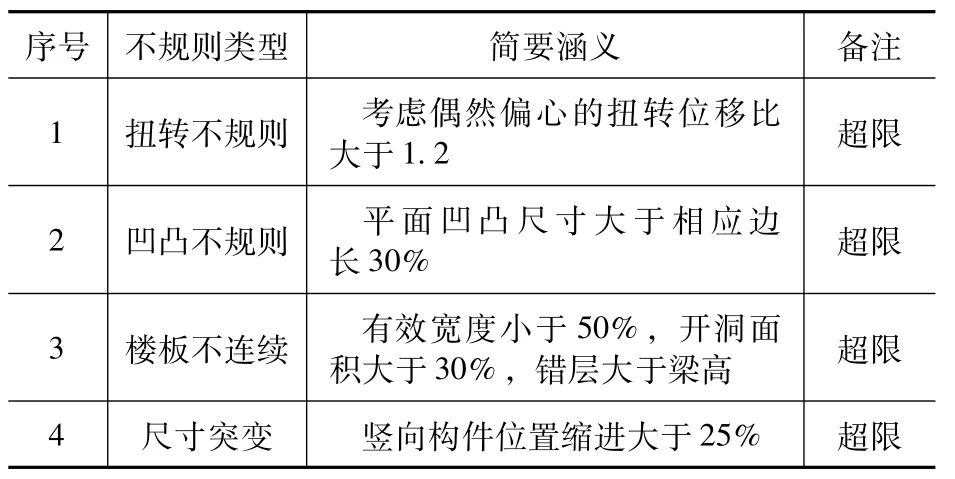
表1 结构超限判定Tab.1 The overrun judgment

现行《建筑抗震设计规范》（GB 50011-2010）［6］（以下简称《抗规》）提出了4 个性能目标、3个地震水准与5个性能水准，并详细定义了每种性能水准结构预期的震后性能状况，《高规》中也有类似规定。根据（表1）超限判定，将此结构抗震性能目标定为C级，即在设防地震作用下关键构件和普通竖向构件发生轻微损坏，而耗能构件发生轻中度损坏，楼板不屈服。

3 结构弹性计算分析

采用PKPM系列软件（2010规范V2.2版）Satwe完成了结构反应谱分析和弹性时程分析，并采用Midas building（2016版）进行了对比计算，然后根据各项弹性分析计算结果（表2～表4），结合规范限值和C级性能目标要求，对结构在风荷载和多遇地震作用下的性能状态进行了评价。

3.1 Midas building分析模型简介

Midas building模型采用集中塑性铰模型模拟梁柱非线性反应。该模型在杆件端部设置0长度的平动和非线性转动弹簧，杆件内部则为线弹性杆，如图2所示，对梁柱单元模型，变形位移都符合小变形假定和平截面假定，Fxi、Fyi、Fzi分别为i端x、y、z方向上的力，Mxi、Myi、Mzi分别为i端绕x、y、z方向上的弯矩，j端同理。

对钢筋混凝土梁单元，假定单元弯矩、轴力、扭矩互不影响，仅考虑弯矩的非线性成分，端部塑性铰滞回模型选取考虑了刚度和强度退化的修正武田三折线模型，其中第一、第二折线拐点分别用于模拟混凝土开裂强度和钢筋屈服强度，如图3 所示，P1（+）、P1（-）表示正向和负向的第一屈服强度，P2（+）、P2（-）表示正向和负向的第二屈服强度，D1（+）、D1（-）表示正向和负向的第一屈服变形，D2（+）、D2（-）表示正向和负向的第二屈服变形。

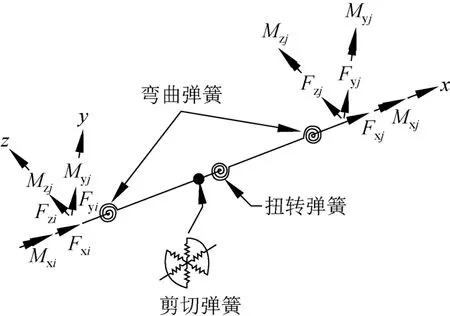
图2 梁柱单元模型Fig.2 The model of beam and column members

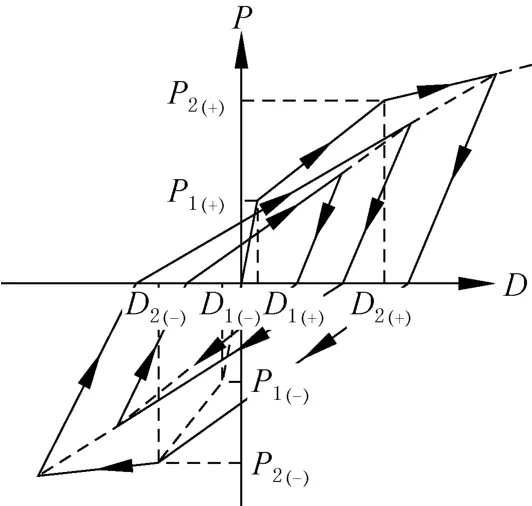
图3 修正武田三折线滞回模型Fig.3 The modified Takeda Hysteretic model

图4 随动硬化三折线模型Fig.4 The kinematic hardening model

参照《高规》7.1.7，对墙肢的截面高度与厚度之比小于4的剪力墙构件采用框架柱单元进行建模设计。对框架柱单元，本文考虑了轴力与弯矩的相互影响，在强度计算时使用变化的轴力并采用随动硬化三折线模型来模拟柱的多轴滞回特性、屈服面特性，如图4所示，其中第一、第二屈服面分别对应构件开裂、屈服状态，P表示轴力，M表示弯矩，N表示变化的轴力，My、Mz表示绕Y、Z方向的弯矩，ε表示轴向应变，φy、φz表示绕Y、Z方向的转角。

对于剪力墙的非线性模拟，Midas building将剪力墙划分为多个非线性单元，每个单元由水平纤维层、竖向纤维层和剪切层组成。

剪力墙材料本构模型如图5。混凝土的材料本构关系采用《混凝土结构设计规范》（GB 50010-2010）附录C中提供的混凝土单轴受压本构模型，εc为峰值应变，εu为极限应变，为峰值应力；钢筋的材料本构关系使用双折线，并认定钢筋为理想弹塑性材料，E1为钢筋初始弹性模量，fyk为钢筋屈服强度标准值，但为了计算的收敛性，第二直线段斜率取E2=0.01E1；墙单元剪切特性材料本构关系使用理想弹塑性模型，G1为墙单元初始剪切模量，τ1为墙单元剪切屈服应力，γ1为墙单元剪切屈服应变。

图5 剪力墙材料本构模型Fig.5 The constitute model of shear wall materials

3.2 结构反应谱分析

结构主振型与周期见表2。

楼层侧移刚度比以及抗剪承载力之比见图6（仅以X方向为例）。根据《高规》3.5.2条，高层建筑需进行相邻楼层侧向刚度比验算。图6a表示X方向本层侧移刚度与上一层侧移刚度的90%、110%或150%的比值（当本层层高大于相邻上层层高1.5倍时采用110%，嵌固层采用150%，其余各层采用90%参与计算）。可以看出，结构抗侧移刚度在收进层（第30层）明显下降，该楼层在弹塑性分析中可能会产生局部塑性变形，结构各层均满足规范对剪力墙结构侧向刚度的要求。

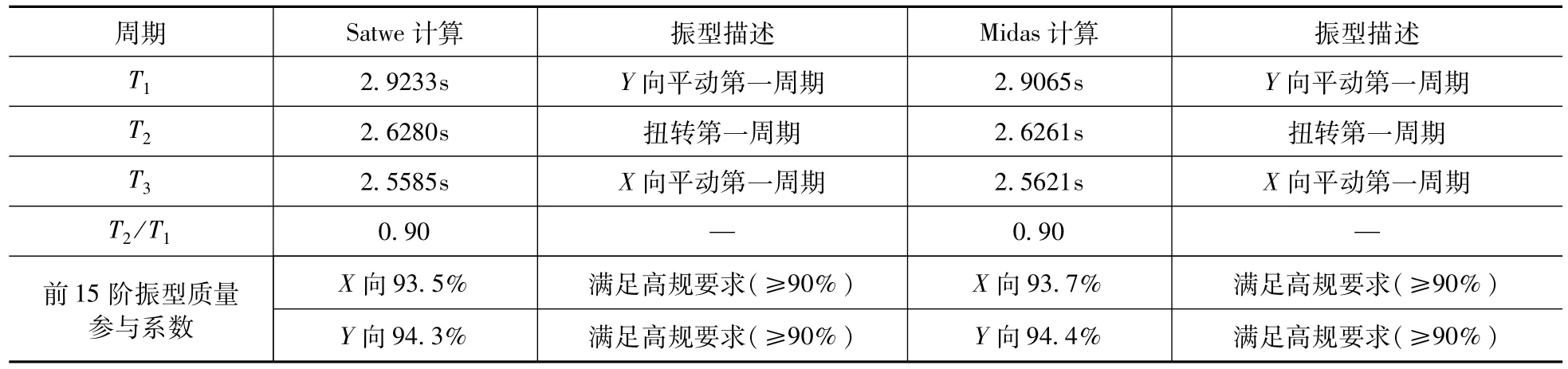
表2 结构主振型与周期Tab.2 The main vibration model and period

图6 楼层X向侧移刚度比及抗剪承载力之比Fig.6 The lateral stiffness ratio and sheer strength ratio

根据《高规》3.5.3条，A级高度高层建筑的楼层层间抗侧力结构的受剪承载力不宜小于其上一层受剪承载力的80%，不应小于其上一层受剪承载力的65%。经计算，如图6b所示，各层均满足高规对抗剪承载力的要求。

基底剪重比、最大层间位移角、位移比、刚重比见表3。

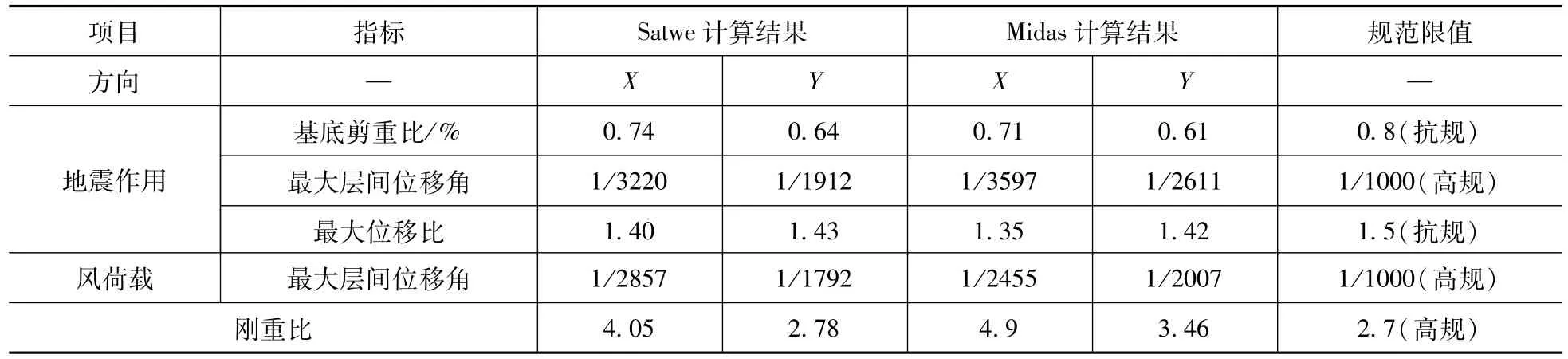
表3 剪重比、层间位移角、位移比、刚重比Tab.3 The ratio of shear to gravity and floor drifts、displacement ratio、ratio of lateral stiffness to gravity

弹性分析结果表明，结构分别在多遇地震和风荷载作用下最大层间位移角为1/1792，明显小于规范限值1/1000，结构保持弹性；结构两个主方向刚重比均大于2.7，能够通过《高规》整体稳定性验算要求，弹性分析时可不考虑二阶效应［7］（刚重比和墙的刚度有关，每个程序对于墙刚度的处理都有些差异，虽然刚重比结果有差异，但结果数据用于判断是否考虑二阶效应还是一致的）；结构底层剪重比均小于规范限值0.8，不满足要求，需对各楼层剪力调整后再进行分析设计。另外，结构扭转周期比和位移比相对较大，其中周期比约为0.9，位移比大于1.4，表明结构在地震作用下存在明显扭转效应，结构竖向收进部位抗扭刚度有待改善。

3.3 弹性时程分析

在此模型基础上又通过Satwe软件完成了结构的弹性时程分析，分析时采用三组加速度时程曲线输入［8］，包括两条天然波USA00684和USA00707［9］，一条人工波RH1TG035；为考虑L型平面平扭耦联效应，采用X、Y双向地震输入，时程曲线峰值加速度按1（X方向）：0.85（Y方向）比例调整［10］；计算分析结果取时程分析法包络值和反应谱分析法的较大值，见表4。

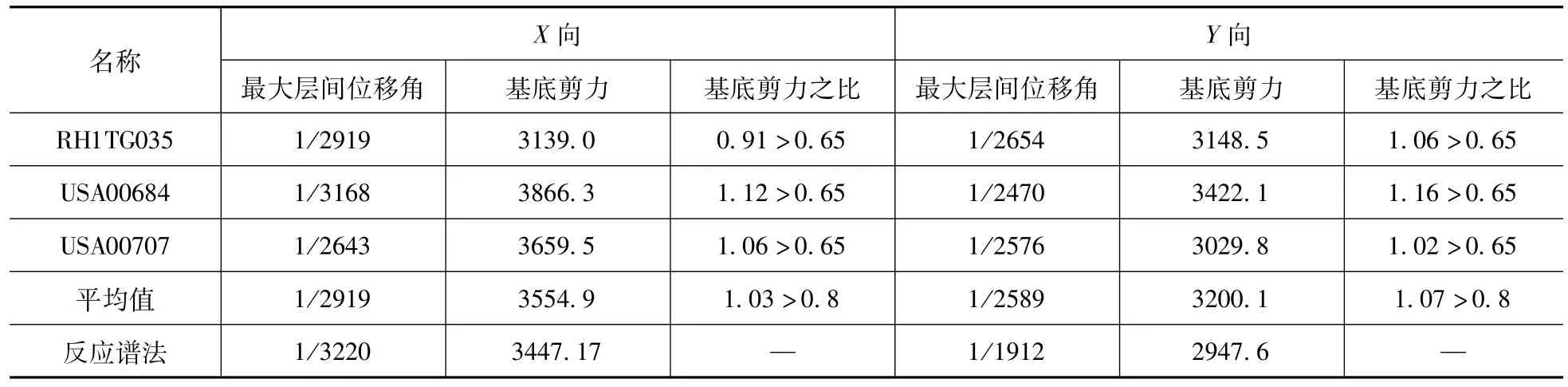
表4 弹性时程分析法与反应谱分析底部剪力对比及层间位移角结果比较Tab.4 The comparison of the base shear between elastic step by step integration and modal response spectrum technique

根据表4可以看出，弹性时程分析法X、Y向的最小底部剪力与振型分解反应谱法计算结果之比为0.91和1.02，大于规范限值0.65，三条地震波X、Y向的平均底部剪力与振型分解反应谱法计算结果之比为1.03和1.07，大于规范限值0.80。由此可以判断所选三条地震波满足《抗规》5.1.2要求，可用于下一步弹塑性时程分析。时程分析法所得基底剪力大于反应谱法计算结果，因此在构件设计时应该采用时程分析法计算结果进行结构的内力计算和配筋。

4 结构弹塑性时程分析

采用Midas building和SAP2000（V17）软件完成了该结构在中震和大震下的弹塑性时程分析［11］，并根据计算结果，分析了结构的非线性反应及破坏机制，进行了抗震性能评价。

4.1 SAP2000分析模型简介

SAP2000中通过线单元中的框架单元模拟结构的框架梁、柱，本文仅考虑框架梁弯矩非线性，采用计算长度为0的集中弯矩塑性铰（Concrete Beams M3）来模拟，其滞回模型同Midas building一致，依然采用修正武田三折线模型，第一、第二折线拐点分别代表开裂强度和屈服强度。

SAP2000中剪力墙的塑性行为是通过分层壳模型的非线性分析来实现的。分层壳单元是基于复合材料力学原理，将一个壳单元分成多层，见图7，每层根据需要设置不同的厚度和材料，一般包括混凝土和钢筋等。钢筋层厚度可以通过实配钢筋均匀“弥散”到一层的原理来换算，并指定材料角来描述钢筋的分布方向。对于混凝土层，可以采用Mander模型来考虑箍筋约束的影响，用以模拟剪力墙边缘构件约束混凝土，见图8，f′cc为约束混凝土强度，f′co为非约束混凝土强度，Ec为混凝土初始切线模量，Esec为混凝土割线模量，εco为非约束混凝土峰值应变，εcc为约束混凝土峰值应变，εcu为约束混凝土极限应变，εt为混凝土峰值拉应变，f′t为混凝土峰值拉应力，εsp表示当应变为2εco时切线与应变轴的交点。

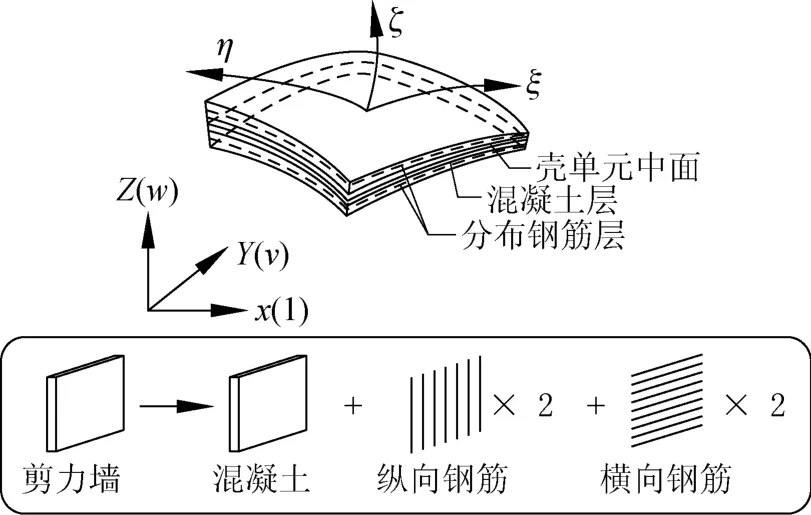
图7 分层壳模型Fig.7 Layer shell model

图8 约束混凝土Mander本构模型Fig.8 The Mander model

4.2 中震、大震下楼层剪力和倾覆弯矩（仅以X方向为例）

在中震和大震作用下，结构的最大层剪力和最大倾覆弯矩均出现在结构底部，如图9所示。其中，中震下结构X向底部最大剪力为9484kN，最大倾覆弯矩为462539kN·m。大震下结构X向底部最大剪力为19055kN，最大倾覆弯矩为997740kN·m。结构层剪力与倾覆弯矩无突变，Y向与X向类似。

4.3 中震、大震下的最大层间位移角

由图10可见，在中震作用下，结构最大层间位移角均小于性能水准3层间位移角限值1/250，满足C级性能目标要求。大震下，除USA00684地震波作用时上部收进楼层Y向弹塑性层间位移角超过高规限值1/120，其余方向各楼层层间位移角均满足规范限值与C级性能目标要求。

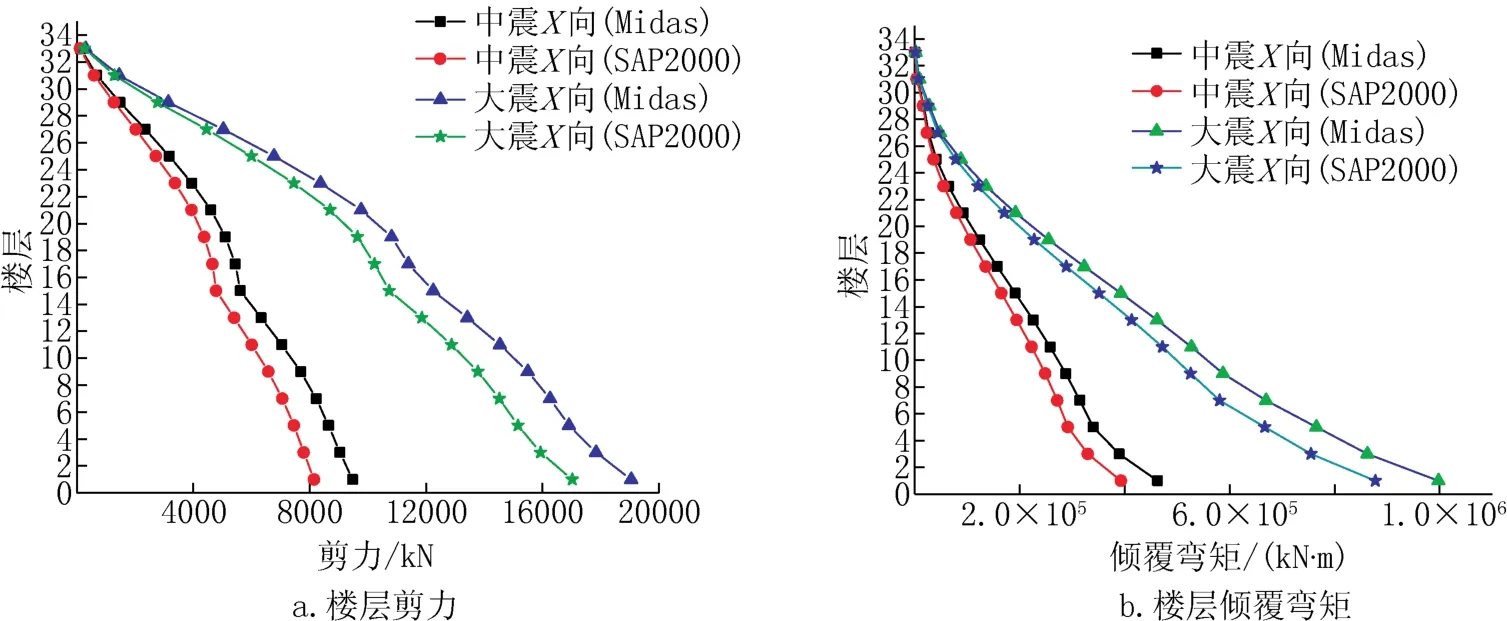
图9 RH1TG035地震波作用下楼层剪力和倾覆弯矩Fig.9 The response envelops of floor shear force and overturning moment under the earthquake of RH1TG035

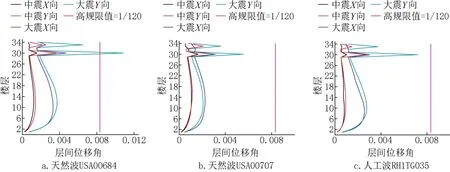
图10 地震波作用下层间位移角Fig.10 The floor drifts under the different earthquake

4.4 结构抗震性能评价

中震及大震作用下，结构各项整体指标满足抗震设计理念及力学反应规律；结构顶部收进部位由于刚度突变，层间位移角增大；结构层剪力与倾覆弯矩竖向均匀无突变，各方向最大层间位移角满足相应性能水准要求。

5 剪力墙结构优化设计

5.1 结构方案优化思路及剪力墙结构优化目标

由于结构的双向偏心率与结构在地震作用下的层间位移比和相对扭转角有明显的相关性，偏心率和位移比越大的结构扭转效应越明显，故以减小结构偏心率并控制弹性计算下的扭转位移比的思路进行优化设计［12］。遵循“强周边，弱中部”概念的设计思路，尽量增强结构周边外围剪力墙，弱化中部剪力墙，控制墙肢轴压比，使其在竖向荷载下接近相应抗震等级的轴压比限值。按照以上思路，对剪力墙进行合理调整（具体优化方案如图11所示），经弹性分析，刚心的位置发生了变化，双向偏心距减小，以期达到减弱结构扭转效应的目的。

图11 剪力墙优化布置方案Fig.11 Optimal layout scheme

5.2 弹性计算结果对比分析

为验证优化方案的有效性，依然采用Satwe软件对其进行弹性分析，并对偏心率、模态、位移比、层间位移角等结果进行对比。

1.双向偏心率

经优化布置，结构双向偏心情况如图11和表5所示，可以看出优化方案有效减小了结构的双向偏心率［13］。

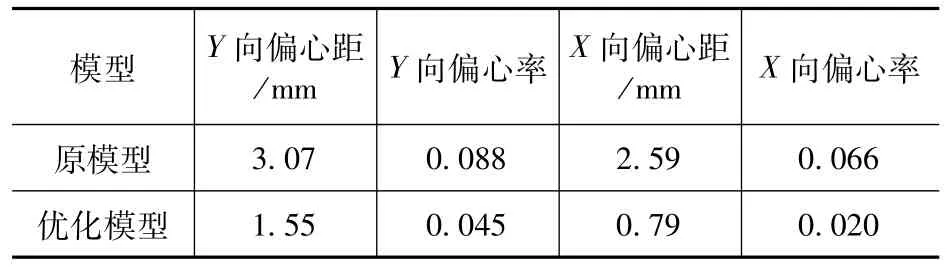
表5 偏心距与偏心率Tab.5 The structure s eccentricity

2.模态分析

原结构和优化模型前三阶振型周期和质量参与系数见表6。

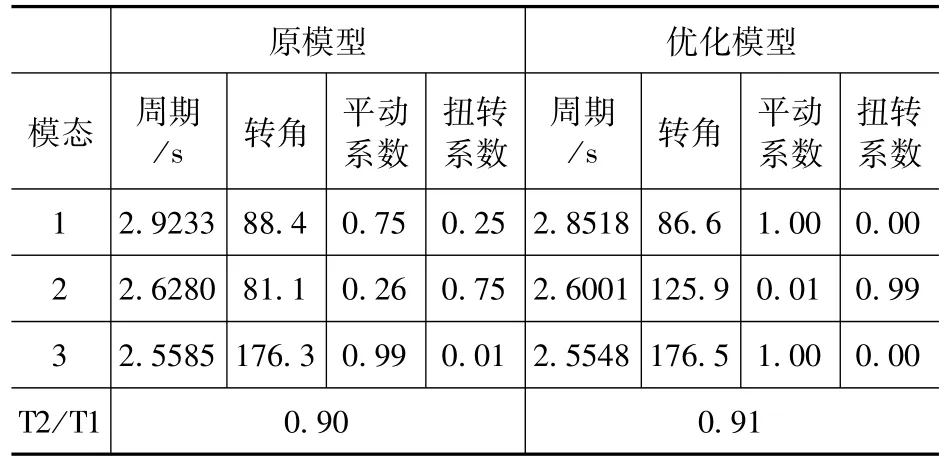
表6 模态分析Tab.6 The model analysis

通过表6可以看出，经过优化布置，前三阶振型基本消除了平扭耦联效应，且Y向刚度有一定提升，表明了控制结构偏心率能有效降低平扭耦联效应。

3.位移比与层间位移角

位移比与层间位移角的对比见表7。

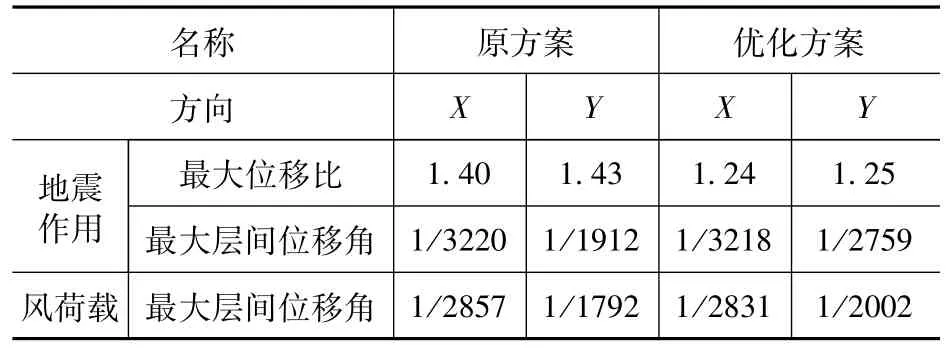
表7 位移比与层间位移角Tab.7 The structure s displacement ratio and displacement angle

经过优化布置，各方向最大位移比和Y方向层间位移角均小于原方案，可见优化方案通过对偏心率的控制，有效地改善了结构位移比和Y方向的层间位移角［14］。

综合以上弹性分析结果可知，轴压比控制不变，通过更为合理的调整剪力墙尺寸，结构整体偏心率明显变小；优化方案基本消除了弹性分析阶段的平扭耦联效应，结构扭转效应得到了有效控制。

5.3 弹塑性时程反应结果对比分析

采用Midas building再次对改进方案进行了建模和大震作用下的弹塑性时程分析［15］，选择USA00684地震波进行大震双向输入工况下的模拟分析，以Y向各结构指标进行对比。

1.结构扭转角

由图12可以看出，经剪力墙优化布置，结构在大震作用下，塑性扭转角自下而上有了显著降低，说明优化方案通过控制双向偏心率，降低了平扭耦联效应和结构位移比，能有效控制结构在大震作用下的塑性扭转变形。

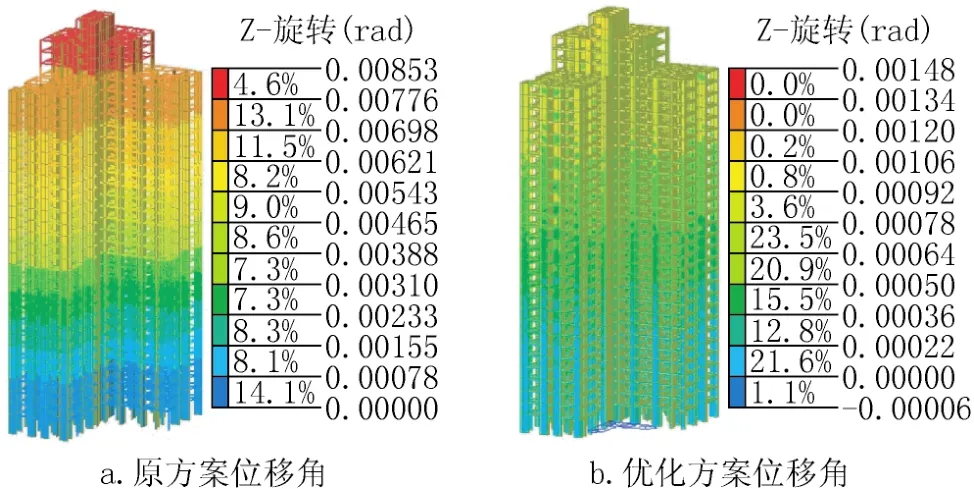
图12 扭转效应对比Fig.12 The comparison of torsion angle

2.结构位移

由图13可以看出，在上部收进部位30层和33层处，优化方案层间位移角显著下降，并满足了高规限值1/120的要求，结合图12扭转角的明显降低，可以判定层间位移角下降的原因主要是结构偏心率降低后，平扭耦联效应减弱，顶层的局部塑性扭转变形显著降低，30层和33层Y向层间位移的主要控制因素由扭转变形变为Y向的平动变形。

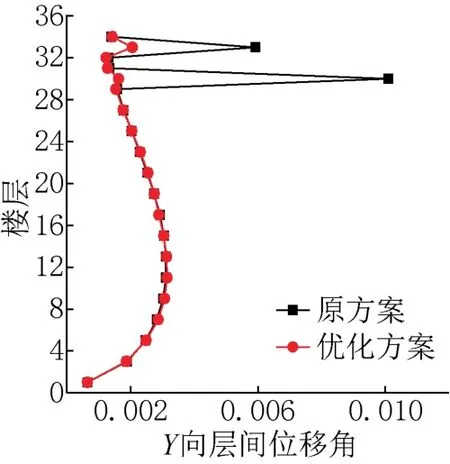
图13 大震下Y向层间位移角Fig.13 The story drift angle under major earthquake

5.4 经济性指标统计对比

经剪力墙优化布置后，混凝土总用量减少43.6m3，钢筋总用量减少740kg，有效地节省了材料用量。两种方案的材料用量对比见表8。

表8 材料用量对比Tab.8 The comparison of material dosage

6 结论

1.结构各项整体指标基本满足规范要求，在小震下作用能保持弹性，达到C级性能目标的要求，但结构扭转周期比和扭转位移比均较大，施工图设计时应采取相应的构造加强措施。

2.中震及大震作用下，结构各项整体指标满足抗震设计理念及力学反应规律，结构顶部收进部位由于刚度突变产生了局部塑性变形，层间位移角增大，结构扭转效应明显且存在部分薄弱构件，应当有针对性地采取相应的构造加强措施。

3.按照减小结构偏心率并控制弹性计算下扭转位移比的优化思路，通过调整剪力墙布置，改变刚心位置，有效地削弱了平扭耦联效应，降低了结构位移比，并取得了一定的经济效益，证明了优化方案的可行性。