一类矩阵的行列式及应用
刘碧铎 胡永建
(北京大学数学科学学院 100871) (北京师范大学数学科学学院 100875)
本文研究n阶矩阵:
(1)
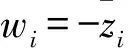
假定zi,wj≠0 (i,j=1,…,n),并记
则Δ(x)为次数不超过n-1的多项式,且Δ(zi)=0 (i=1,…,n-1).因此,Δ(x)=c(x-z1)…(x-zn-1),其中c为常数.令x=0,则c=(-1)n-1·(z1…zn-1)-1Δ(0). 注意到,
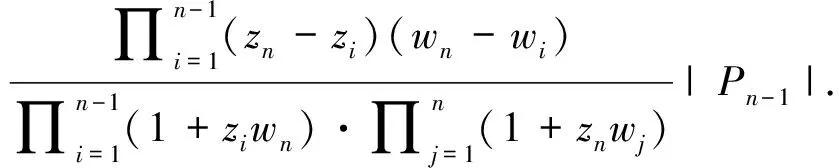
(2)
根据递推式(2),我们可证明如下结论:
定理1设矩阵Pn由(1)式给出.则Pn的行列式为
(3)
证明由定理1前面的分析知,当zi,wj≠0 (i,j=1,…,n)时,递推式(2)成立,由此不难得到(3)式成立. 当某两个zi或某两个wj等于0时,则Pn的两行或两列相同,从而|Pn|=0,此时(3)式仍然成立. 当某个zi或wj等于0时,(3)式等号左右两边的表达式关于zi,wj在zi=0或wj=0处连续.那么,令zi→0或wj→0,可以推出当zi=0或wj=0时(3)式也成立.证毕.
由定理1知,矩阵Pn总是非奇异的. 特别地,如果zi(i=1,…,n)是复平面单位开圆盘内互异的点,则Pick矩阵
为Hermite正定矩阵.
k,l=1,…,n.
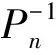
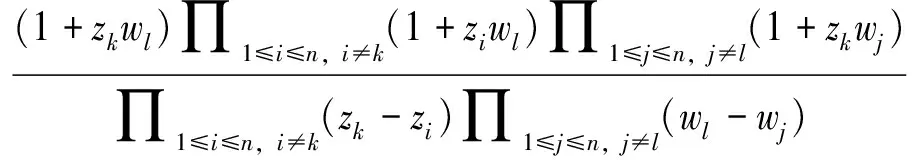
于是,我们有下面的结论:
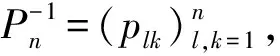
plk=(-1)n-1·
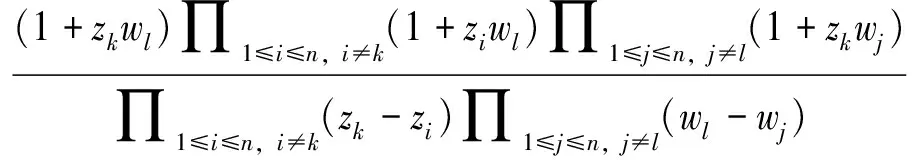
l,k=1,…,n.
利用定理1的结论,可以得到美国数学月刊第11969号问题的一个简单解答.
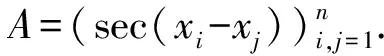
(4)
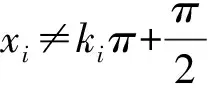
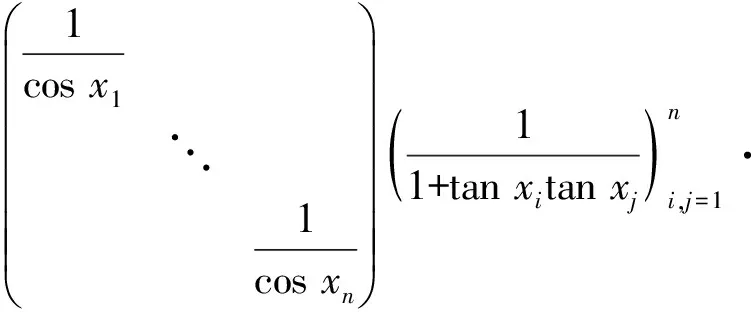

由定理1知,
众所周知,Cauchy矩阵是如下形式的矩阵:
(5)
其中x1,…,xn与y1,…,yn分别互异,且xi≠-yj(i,j=1,…,n). 由定理1还可以得到Cauchy矩阵Cn的行列式表达式、可逆性的证明和逆矩阵的表示[3].
推论1设Cn由(5)式给出,则Cn的行列式为
(6)
证明首先假定x1,…,xn≠0,则
由定理1的结论可知,
当某两个xi=0时,Cn中出现两行相同,则|Cn|=0,(6)式成立. 当某个xi=0时,注意到(6)式等号两边的表达式在xi=0处有定义且连续,令xi→0,则(6)式仍然成立. 证毕.
由定理3知,Cauchy矩阵Cn总是可逆的. 容易发现,Cn中每个元素的余子阵是n-1阶Cauchy矩阵.据此可以得到Cn的逆矩阵的如下表示.
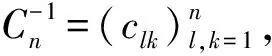
clk=
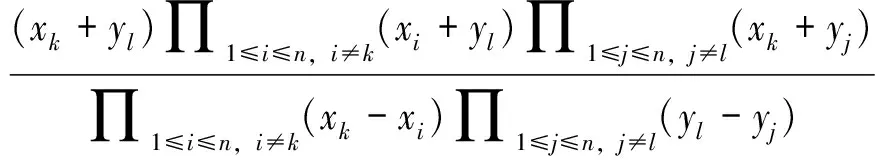
l,k=1,…,n.
例2设矩阵
证明:A为可逆矩阵且A-1为整数矩阵.
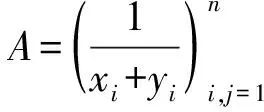
=(-1)k+l·
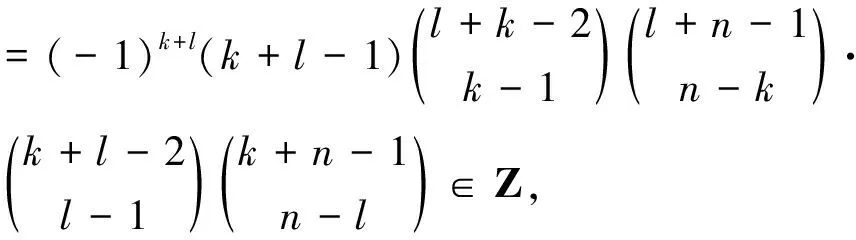
故结论成立. 证毕.

