关于循环和与循环积不等式
蒋 迅
谈到不等式,有两个著名的不等式是我们都非常熟悉的:一个是算术平均-几何平均不等式,另一个是柯西-施瓦茨不等式.给定2n个实数a1,a2,…,an和b1,b2,…,bn我们分别有:
和
≥(a1b1+a2b2+…+anbn)2,
如果用求和符号∑和求积符号∏来表达的话,那么它们分别可以写成:
和
这两个不等式都有一个共性,那就是在求和以及求积时每个单项具有循环性.所以我们可以用∑和∏来简化.我们还可以用另一种方式来表达, 即明确地指出求和是对每一个单项循环求和,求积是循环对每一个单项求积.
f(a1,a2,…,an)+f(a2,a3,a4,…,an,a1)+…+f(an,a1,a2,…,an-1).
f(a1,a2,…,an)·f(a2,a3,a4,…,an,a1)·…·f(an,a1,a2,…,an-1).
其中“cyc” 是英文“cyclic”的缩写,意为“循环的”.
按照这个定义,算术平均-几何平均不等式和柯西-施瓦茨不等式也可以记作:
和
甚至可以简化成
和
引入循环和及循环积的概念后,我们可以讨论更为广泛的不等式.这类不等式表达简洁,而且在奥数竞赛中经常出现.让我们来看几个例子.限于篇幅,我们只考虑n=3的情形,并给定三个实数a,b和c.我们将限制到上述两个经典不等式的应用上,顺便介绍一些国外的数学竞赛和网站.下面所有的例子均取自Alexander Bogomolny博士建立的网站https://www.cut-the-knot.org. 这个网站内容及其丰富,特向数学爱好者和数学老师强烈推荐.
例1[1](2017年加拿大奥数)设a,b和c非负并两两不同.则

证明注意循环性质,我们可以假定a>b>c.令x=a-b,y=b-c,则x>0,y>0. 由算术平均-几何平均不等式,我们有
例2[2](罗马尼亚数学杂志) 设a,b,c>0. 则
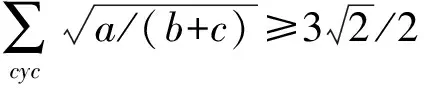
证明这个不等式可以用循环不等式来表示.让我们用这种表达形式来给予证明.事实上,由算术平均-几何平均不等式,我们有
例3[3](1967年国际奥数备选试题)设a,b,c>0. 则
说明这道题目是国际奥数(IMO)在1967年的备选题,由波兰提供.从这道题,我们可以清楚地看到,具有简约之美的题目受人喜爱.2016年国际奥数备选题中也有一道是(带限制条件的)循环和与循环积的不等式[4].国际奥数委员会在每一届竞赛过后都会有备选题及解答.这些试题可以在其官网https://www.imo-official.org/上找到.
证明记
再记
g=a8+b8+c8-a3b3c2-a3b2c3-a2b3c3.
则显然只须证明g≥0. 类似于例1我们看到,由于循环对称性,我们可以假定a≥b≥c. 令b=c+ε,a=c+δ+ε, 其中ε,δ≥0. 将b和c的上述两个表达式代入g并展开,然后合并同类项.我们将发现所有的负号项都被消去.细节从略.
例4[5](1997年国际城市数学竞赛高中组) 设a,b,c>0. 则
说明城市数学竞赛(Tournament of the Towns)始于1980年,原只有前苏联的三个城市莫斯科、基辅及里加市参加,现已成为国际性的比赛,由俄罗斯科学院主办,有上百个城市,数十万名学生参加.
证明应用算术平均-几何平均不等式,我们有
注意最后的循环和变成了简单的代数表达式.这也是此类不等式证明中的常用技巧.
例5[6](校园奥数)设a,b,c>0. 则
说明“校园奥数”(Olimpiada pe Scoala)是脸书上的一个数学群,里面聚集着众多的数学爱好者.这个解答由其成员Diego Alvariz提供.脸书的群与微信的群有相似之处,但我个人认为好很多.首先脸书没有500会员的限制;其次,脸书的群中成员可以只讨论你感兴趣的贴,这一点有点像微博.
证明由柯西-施瓦茨不等式我们有
例6[7](罗马尼亚数学杂志) 设a,b,c>0. 则
说明我们在前面已经介绍过“罗马尼亚数学杂志”.这个题目在Bogomolny的网站上有误.正确的题目在这里:http://www.ssmrmh.ro/wp-content/uploads/2017/01/1515-31.jpg,此解是由罗马尼亚人Mihalcea Andrei Stefan解出的.
证明将不等式两边同除以abc,我们得到一个等价的不等式
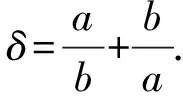
或
4δ2-δ-14=(δ-2)(4δ+7)≥0.
由算术平均-几何平均不等式,我们知道δ≥2. 问题得证.我们看到,这个证明其实是把一个循环不等式分解成了三个独立的不等式.这种方法不常见,但也不能完全忽略它.
例7[8](一个国际合作的循环不等式)设a,b,c>0. 则
说明这个问题是由尼日利亚大学工程系硕士生Uche Eliezer Okeke提供给旅美俄国犹太裔数学家Alexander Bogomolny的.后者在他的网站上提供了来自多国的五个解答.我们这里选用的是越南人Hung Viet Nguyen给出的证明.所以我把这个不等式叫作一个国际合作的循环不等式.说到这位越南人,还有他的一个不等式[9].设a,b,c>0. 则
这是Nguyen Viet Hung在脸书的“Solving the Inequality”群里发的一道题.他声称这是一个经典的不等式,Bogomolny赞其“纯粹的优雅”,但它似乎并不为众所周知.这个群有5500多人,聚集着众多高手.
证明首先,我们用算术平均-几何平均不等式三次得到
如果我们能够证明
那么,
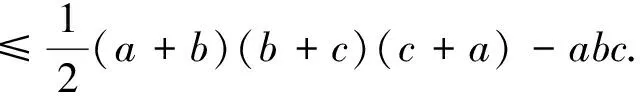
注意到
(a+b+c)2≥3(ab+bc+ca),
8(a+b+c)(ab+bc+ca)≤9(a+b)(b+c)(c+a).
我们得到
例8[10](一个带限制条件的循环不等式)设a,b,c>0 并设a+b+c=1. 则
说明带限制条件的循环不等式有很多.这类问题在极值优化方面有广泛应用.我们仅举这一个例子.这道题是由罗马尼亚数学会的Leo Giugiuc发表在CutTheKnotMath脸书群里的.给出了6个解答.这里的解答是由罗马尼亚人Marian Cucoanes做出的.
证明这个不等式等价于(a+1)(b+1)(c+1)≥64abc. 将1换成a+b+c,我们又得到一个等价的不等式

再由算术平均-几何平均不等式,我们有
上面三个不等式相乘给出最后的结论.
例9[11](双三组数的循环不等式)给定a,b,c,x,y,z∈R,xyz≠0. 则
注本题最早发在罗马尼亚数学杂志上,后来由Dan Sitaru转发到CutTheKnotMath脸书群里.这个解答由印度人Ravi Prakash提供.本题看似复杂,但其实做起来只用到一些代数运算.在给出证明之前,我们为那些可能有些失望的读者提供一个带限制条件的双三组数的循环不等式[12].设a,b,c,x,y,z>0并且(ab+bc+ca)(xy+yz+zx)=1. 则
证明对题目中的不等式的左边展开再做完全平方,我们有
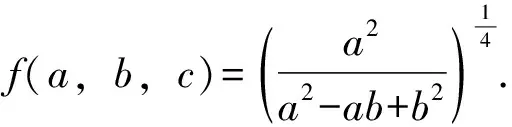
f(a,b,c)+f(b,c,a)+f(c,a,b)≤3.
说明“美国数学月刊“是美国数学协会发行的一个面向大学生的刊物,每年10期.它每期都有一个问题征解栏目.特别受读者欢迎. 这道题由希腊人George Apostolopoulos提供,Leo Giuguic提供了解答.
引理1对于x≥0, 有不等式
引理2设a,b,c>0. 则
9abc≤(a+b+c)(ab+bc+ca).
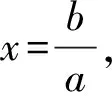
类似地,
所以我们只需要证明
注意到
我们可以用柯西-施瓦茨不等式得到
再由引理2,
8(a+b+c)(ab+bc+ca)
≤9[(a+b+c)(ab+bc+ca)-abc]
=9(a+b)(b+c)(c+a).
于是,
本文通过对一些实例的讨论介绍了循环和与循环积不等式.这些例子的证明显示了在这类不等式中常用的技巧,比如循环对称的性质及积和互化.本文还介绍了一些国外社交网络上数学爱好者的活动,希望对国内的读者有所帮助.

