欧拉不等式的一个加强的改进

刘其右　郭要红

(安徽师范大学数学计算机科学学院　241003)

近年来，对欧拉关于三角形的外接圆半径R与内切圆半径r的著名不等式R≥2r的隔离、加强与推广研究精彩纷呈.文[1]给出欧拉不等式与边长间的一个不等式链，文[2]建立了欧拉不等式的如下三角形式的加强不等式.

定理1设R,r分别为△ABC的外接圆半径与内切圆半径，则有(∑表示循环和)

(1)

当且仅当△ABC为正三角形时取等号.

文[3]将不等式(1)加强为：

定理2设R,r分别为△ABC的外接圆半径与内切圆半径，则

(2)

类比不等式(2)，文[3]得到欧拉不等式的如下三角形式的加强式：

定理3设R,r分别为△ABC的外接圆半径与内切圆半径，则

(3)

当且仅当△ABC为正三角形时取等号.

本文将不等式(3)加强为：

定理4设R,r分别为△ABC的外接圆半径与内切圆半径，则

(4)

当且仅当△ABC为正三角形时取等号.

证明设s是△ABC的半周长，

不等式(4)等价于

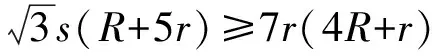
⟺3s2(R+5r)2≥49r2(4R+r)2

只需证明

≥49r2(4R+r)2，

⟺6(2R-r)(R+5r)2≥49Rr(4R+r)

⟺12R3-82R2r+191Rr2-150r3≥0

⟺(12R2-58Rr+75r2)(R-2r)≥0，

(5)

由欧拉不等式R≥2r，

(12R2-58Rr+75r2)(R-2r)

所以，(5)式成立，于是，(4)式成立.

与定理2相比较，一个自然的、需要研究的问题是：

问题设R,r分别为△ABC的外接圆半径与内切圆半径，使得

成立的λ最大值是多少？