文化视角下平方差公式的教学*

吴现荣　姚绍柳　蒙艳虹

(1.黔南民族师范学院数学与统计学院　558000; 2.贵州省三都县第三中学　558000)

在几千年的社会发展过程中，数学逐渐形成了独特的数学文化，数学文化对人类的发展产生了重大的、非物质化的影响，数学文化影响人的观念、思想和思维方式，在数学发展的过程中，人类表现出来的进取精神和崇高境界也是数学文化的重要组成部分.课标中强调指出：“……数学是人类的一种文化，它的内容、思想、方法和语言是现代文明的重要组成部分.”[1]数学文化具有十分丰富的内涵，不同民族的风土人情、文化氛围和教育传统有着很大的差异性.水族是一个具有悠久历史文化传统的民族,主要聚居在贵州的三都水族自治县，水族学生数学学习兴趣均值得分为1.716分， 85%水族初中生认为数学学习比较难或者很难，对数学学习感兴趣和很感兴趣的占28.9%[2].因而在水族地区的数学教学过程中，应结合水族地区学生的心理发展特征、兴趣爱好、认知规律和个体差异，探索民族文化与现行中小学数学教材内容的有效融合，按照国家数学课程标准的要求，对于国家统一的数学教科书内容进行选择、重组，让水族地区学生感受到数学是有趣的，他们认识到数学不仅源于生活，而且用于生活，生活中处处有数学，数学中也处处有生活．本文以平方差公式的教学为例，借鉴民族文化和数学史，营造不一样的课堂.

1　材料选取

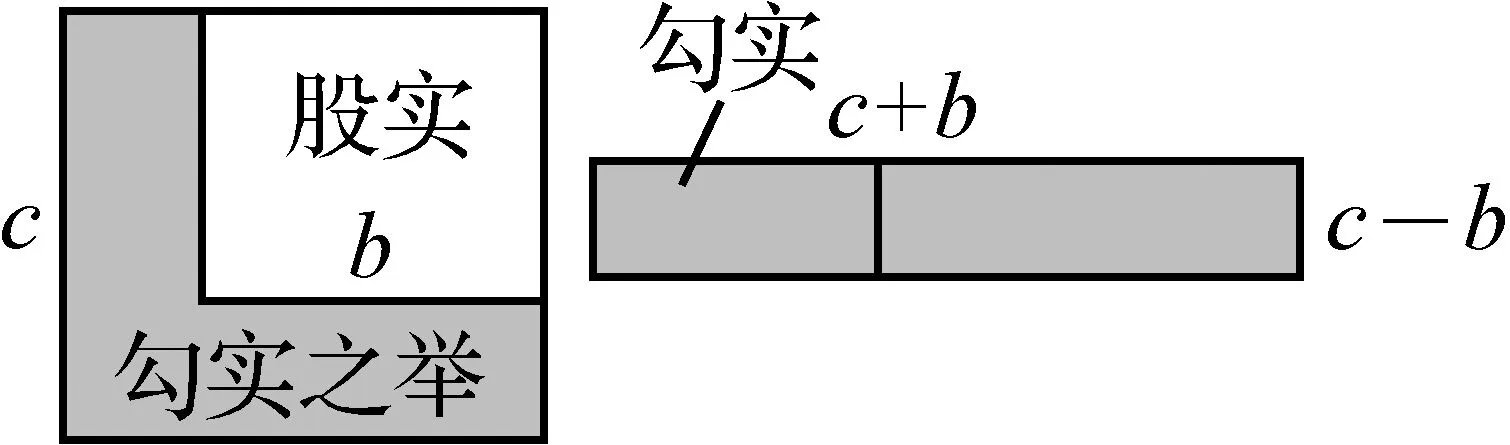
图1

图2

平方差公式蕴含了丰富的民族文化背景.水族文化源远流长，有被誉为“古文字活化石”的水书，也有被誉为“刺绣中的活化石”的马尾绣，还有剪纸、银饰、蜡染、服饰、铜鼓、芦笙等绚丽多彩的水族文化，如图3所示，其中鞋垫的纹理、马尾绣背带心、吃饭的桌子、服饰绣片纹理中都蕴含有平方差公式.

图3

2　教学设计与实施

2.1　渗透文化 发现公式

教师用PPT展现某同学的前测问题的解答：

图4

问题：如图4从边长为a的正方形纸片中剪去一个边长为b的小正方形，你可以把阴影部分拼成什么图形？并将阴影部分的面积用含a,b的代数式表示出来.

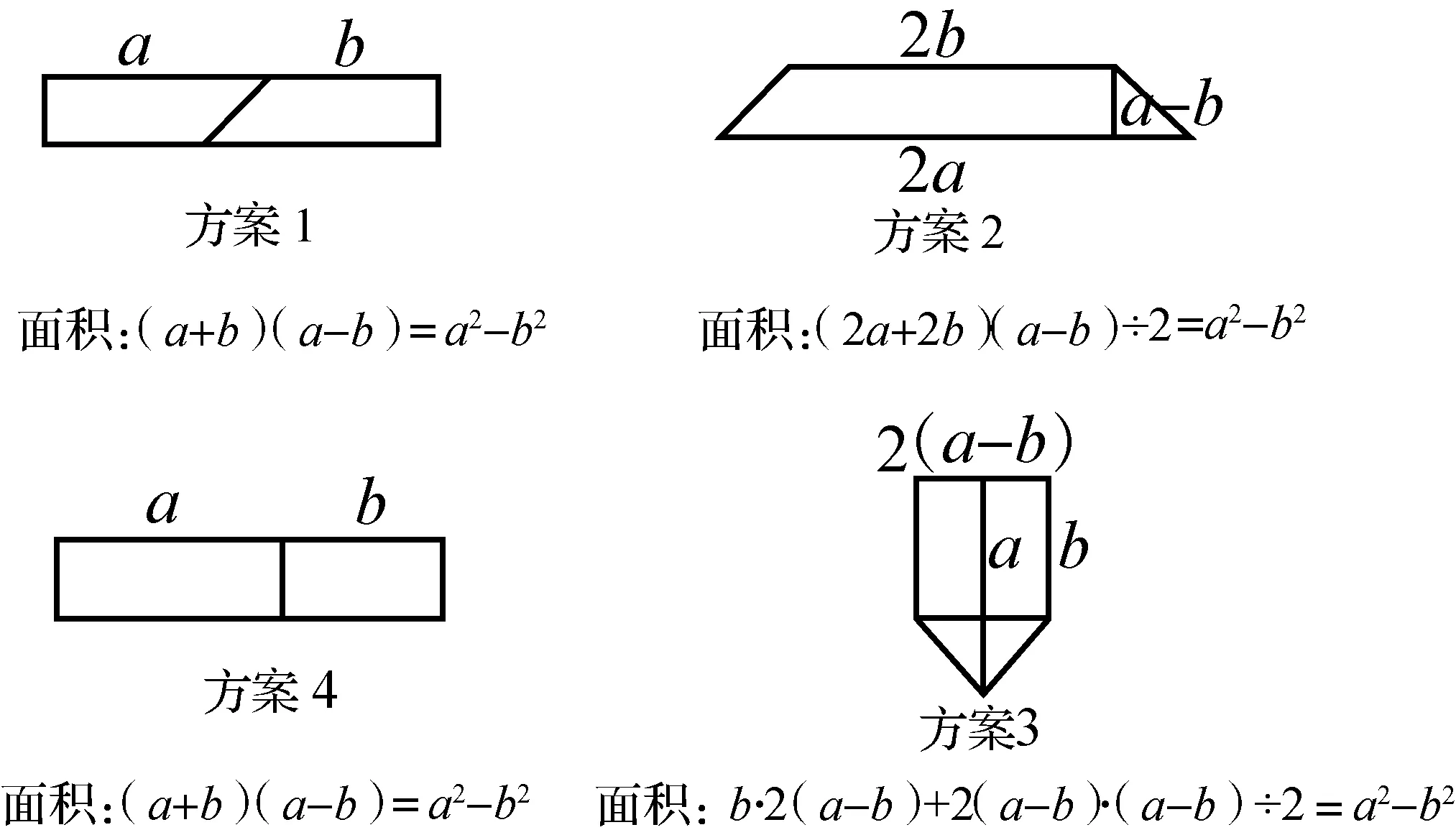
图5

师：观察该同学的四种方案，方案1和方案4均可得面积关系(a+b)(a-b)=a2-b2，那么方案2和方案3是否也有这个面积关系(a+b)(a-b)=a2-b2？

生：(2a+2b)(a-b)÷2=(a+b)(a-b)

=a2-b2;

b·2(a-b)+2(a-b)(a-b)÷2

=(a+b)(a-b)=a2-b2.

师：这种方法是公元3世纪中国古代数学家赵爽的“面积割补法”，教师用PPT展示并介绍赵爽的“面积割补法”，面积割补的证明方法最早是由我国三国时代的数学家赵爽想出来的.赵爽在注释《周髀算经》中的“勾股圆方图”时说：“勾实之矩以股弦差为广，股弦并为袤，而股实方其里.……股实之矩以勾弦差为广，勾弦并为袤，而勾实方其里.” 如图1所示，在以边长为c的正方形中作一个边长为b的正方形，则余下的矩形面积等于一个以c+b为长、c-b为宽的矩形面积.

设计意图通过问题驱动学生课前学习，以展示学生成果的方式进入课堂，增强学生的自信心，激发数学学习兴趣.通过介绍赵爽的“面积割补法”，让学生掌握知识之源，引发情感之悦.

师：将小正方形放在大正方形的正中央是否还会有这样的结果？

图6

教师展示学生熟悉的如图6所示的马尾绣背带心(背带心是由四块全等且底角为45°的等腰梯形绣片和一个正方形块绣片拼接而成)，若已知背带心的边长为a和中间正方形块绣片的边长为b，你能将四块等腰梯形绣片拼成什么图形？如何求这四块等腰梯形绣片的面积？

师：将准备好的彩色纸片分发给六个小组的学生.

生：各个小组通过拼图游戏活动，将拼好的图形贴在教室的黑板上，并求出这四块等腰梯形绣片的面积.

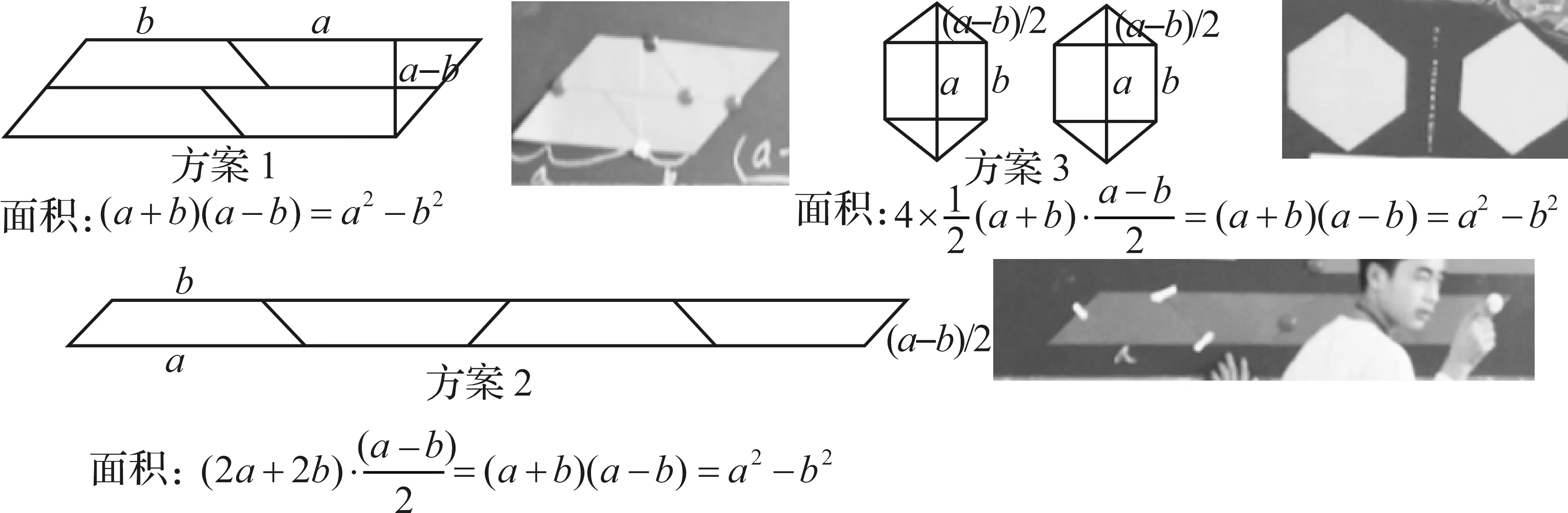
图7

生：第三小组拼好的图形如图7的方案1所示，所求面积为

(a+b)(a-b)=a2-b2.

生：第六小组拼好的图形如图7的方案2所示，所求面积为

生：第二小组拼好的图形如图7的方案3所示，所求面积为

师：将小正方形放在大正方形的正中央，如图7所示，通过如上三种方案我们同样可得面积关系(a+b)(a-b)=a2-b2.

设计意图通过渗透水族文化的神奇魅力和精髓，建立数学与水族文化之间的联系，让学生体会本民族文化的价值，增强学生的民族自豪感，激发数学学习兴趣.通过拼图活动和小组合作交流的方式发现平方差公式，可以促进学生发展“直观想象”的核心素养.

2.2　剖析公式 揭示本质

师：前面我们从“形”的角度发现(a+b)(a-b)=a2-b2，那么我们能否从“数”的角度(多项式的乘法运算)验证：(a+b)(a-b)=a2-b2.

生：(a+b)(a-b)=a2-ab+ba-b2=a2-b2.

设计意图运用数形结合的数学思想方法对平方差公式进行“猜想—验证”，在学生已掌握多项式的乘法法则基础上，教师启发引导学生通过对特殊多项式相乘的计算，既复习了旧知，又为接下来公式的剖析作铺垫，全方位、多角度发现平方差公式，进而培养学生的发散思维.

师：(a+b)(a-b)=a2-b2称为平方差公式.

师：你能用文字语言表述该公式吗？

生：两个数的和与这两个数的差的乘积等于这两个数的平方差.

师：引导学生观察公式的结构特征：

公式的左边是两个二项式相乘，其中“a与a”是相同项，“b与-b”是相反项；右边是二项式，是相同项与相反项的平方差a2-b2.且a与b可以是数，也可以是式.

设计意图引导学生从“相同项”与“不同项”的视角对平方差公式的结构特征加以归纳概括，实现文字语言与符号语言的相互转化，促进学生发展“数学抽象”的核心素养.

2.3　巩固应用 内化新知

例1判断对错，如果有错，如何改正？

(1)(a+b)(b-a)=-a2-b2;

(2)(-x+2y)(-x-2y)=-x2-4y2;

(3)(-5x-3)(5x-3)=25x2-9;

(4)(4x+3b)(4x-3b)=16x2-9;

(6)(x-2a+1)(x+2a-1)=x2-4a2-1.

解(1)(a+b)(b-a)=-a2-b2(错；改正：(a+b)(b-a)=-a2+b2);

(2)(-x+2y)(-x-2y)=-x2-4y2(错；改正：(-x+2y)(-x-2y)=x2-4y2);

(3)(-5x-3)(5x-3)=25x2-9(错；改正：(-5x-3)(5x-3)=-25x2+9);

(4)(4x+3b)(4x-3b)=16x2-9 (错；改正：(4x+3b)(4x-3b)=16x2-9b2);

(6)(x-2a+1)(x+2a-1)=x2-4a2-1

(错；改正：(x-2a+1)(x+2a-1)=x2-(2a-1)2=x2-4a2+4a-1).

该例教师用PPT出示题目，每个小组推荐一名同学讲解，完成情况较好.

设计意图该例是针对学生课前练习中出现的错误进行再次呈现，考查学生对平方差公式的结构特征的理解，给学生自我评价的机会，也对学习效果进行及时的检测，让学生真正掌握平方差公式中的a,b可以是数，也可以是单项式、多项式等代数式，即在指代具有“广泛性”的理解上可促进学生发展“数学建模”的核心素养.

例2绣一幅马尾绣背带需要102克马尾，每克马尾98元，求绣一幅马尾绣背带需要多少钱？

该例由于有多数学生是直接列式计算，没有用如下简便方法进行计算:

102×98=(100+2)(100-2)=1002-22

=10000-4=9996.

设计意图该例是立足课本进行变式引申，通过设计适合水族学生的情景问题，将水族文化有效融入平方差公式的变形应用中，符合水族学生的生活实际和心理特征.在问题解决过程中，借鉴知识的历史，加深学生对平方差公式的理解和灵活应用，培养学生的发散思维.

2.4　拓展深化 发展思维

问题：已知两个正数的和为10，积为21，求这两个数.

设计意图该问题在解决过程中，借鉴数学的历史，加深学生对平方差公式的理解和应用，培养学生的逆向思维和逻辑思维.

2.5　课堂小结 提升内涵

下课临近，教师提出如下三个问题：

(1)你还能举例说明平方差公式在水族文化中的应用？

(2)通过这堂课，当你看到“平方差公式”这几个字时，你会想到什么？

(3)这节课你印象最深的是什么？

关于第一个问题，学生的回答：马尾绣背带、鞋垫的花纹、窗子、吃饭的桌子、烤火的火盆、房子……

关于第三个问题，部分学生的回答如下：

生1：课堂上，大家一起动手拼图，一起探索发现公式，使课堂生动起来;

生2：我们组的成员都很积极，老师的教学方式变了，讲了我们的水族马尾绣，我们是在欢语中度过这节课的；

生3：我认为赵爽是一个伟大的数学家，他的面积割补法让我在拼图游戏中学到数学知识，让我学会动手、动脑解决数学问题；

生4：马尾绣背带中也有平方差公式，我们水族的祖先挺厉害的；

生5：本节课中我认识了很多数学家，但是教师介绍丢番图所采用的“和差法”，其解法我还是不明白；

生6：课本中的例题也有历史，老师介绍古希腊数学家欧几里得在《几何原本》中公式，以后我会用公式进行简便运算了……

2.6　布置作业

1.必做题(教材习题14.2)：

(1)运用平方差公式计算

2.选做题

(1)村长把一块边长为a(a>10)米的正方形土地租给爷爷.第二年，他对爷爷说：“我把这块地的一边减少10米，相邻的另一边增加10米，继续租给你，租金不变.爷爷吃亏?为什么？

(2)计算：20082-2009×2007；

(3)请同学们以吃饭的桌子为例，提出与平方差公式相关的问题.

设计意图作业分层处理，尊重学生的个体差异，满足多元化的学习需要，让不同基础的学生得到不同的发展.布置与水族文化有关的作业，让学生认识到数学不仅源于生活，而且用于生活.

3　调查反馈

课后，对全班47名学生做了问卷调查.对于问题“你喜欢数学的历史吗？”，有6人回答 “非常喜欢”，有33人回答“喜欢”，占82.9%；对于问题“你喜欢水族文化吗？”,有23人回答 “非常喜欢”，有22人回答“喜欢”，占95.7%；对于问题“三国时期数学家赵爽，你______.”36.2%回答“没听说过”；对于问题“关于《周髀算经》，你______.” 80.9%回答“没听说过”；关于“关于古希腊数学家丢番图，你________”，53.2%回答“没听说过”；关于“关于欧几里得的《几何原本》，你________”，36.2%回答“没听说过”； 91.5% 的学生希望将本民族文化渗透在教材中；而在以往的数学课堂中老师基本不渗透水族数学文化和数学史.

4　结语

民族地区的数学教学具有民族特色，而数学本身是自然的，自然源于它的历史和生活实际，将民族文化与数学的历史有效渗透于平方差公式的探究、发现、推导、证明、应用过程，使平方差公式的教学变得自然而然，加深学生对平方差公式的理解和掌握，拓宽了学生的思维，从而揭示了“知识之谐”，展现了“方法之美”，凸显“文化之魅”.该课学生以拼图游戏的方式进入课堂，让学生自主探究发现平方差公式，使学生真正成为课堂的主人，学生会变得更加乐学，激发了“情感之悦”，达到水族地区数学教学的“德育之效”.