洛仑兹变换与狭义相对论之间的数学矛盾
郭峰君
(国家电网公司辽宁省抚顺供电公司 113001)
洛伦兹变换(简称为洛变)是狭义相对论(简称为狭相)的数学灵魂,狭相的诸多结论都建立在洛变基础上.本文旨在利用数学证明方法揭示出洛变与狭相的诸多结论之间存在着的不可调和的数学矛盾,让广大读者彻底看清狭相的真实面目.
一、洛仑兹变换与伽利略变换
狭相认为,洛变
在v≪c条件下可被约化为所谓的伽利略变换,即
x′=x-vt、y′=y、z′=z、t′=t.
然而,通过数学证明得出结论:洛变在v≪c条件下的近似解和在v/c→0条件下的极限解皆非如此.

故若只保留其中第一项有效,则洛变的近似解为
若设v/c→0,则有
因在洛变中c为常数,故v/c→0实质就是v→0.
二、狭义相对论的多普勒原理



若根据狭相关于洛变在v≪c条件下的逻辑,则其近似解应为T′≈T(或f′≈f)和λ′≈λ±vT.
三、狭义相对论的速度关系式
将洛变改写为微分形式
并用前三式分别除以第四式,再设
最后得到
式组(1)中第一式被称为狭相的速度关系式.
根据狭相的光速不变原理,又有
x2+y2+z2=c2t2、x′2+y′2+z′2=c2t′2.(2)
将式组(2)中第一式改写为微分形式
(dx)2+(dy)2+(dz)2=c2(dt)2,
再将等式两边都除以(dt)2,最后得到
ux2+uy2+uz2=c2.(3)
将式组(2)中第二式改写为微分形式,最后得到
ux′2+uy′2+uz′2=c2.(4)
将式组(1)代入式(4),即
可得到式(3).根据式(3)和式(4)可知:因ux、uy、uz和ux′、uy′、uz′都是c在三维直角坐标系中各相对应的坐标轴上的分量,故若uy≠0或uz≠0,则必有ux 因电磁波属于横波,故在三维直角坐标系中可将电磁波一维波动方程写为 一起代入式组(5),可得到 洛变可能仅仅是满足电磁波一维波动方程协变的部分数学条件,且其中的y′=y、z′=z是多余的. 将满足电磁波一维波动方程协变的数学条件写为 似乎更为简明且适合.四、洛伦兹变换与电磁波一维波动方程
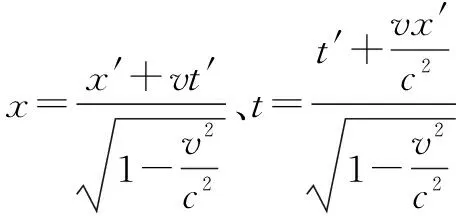
五、满足电磁波一维波动方程协变的数学条件

