“数系扩充”的课堂“扩充”

孙传正

(江苏省南京市人民中学　210000)

一、数系：理应扩充

1. 理念重温

本节课旨在让学习者回顾数系的扩充过程，进而激发学者探索欲望.本节课学习之前，学生的知识储备停留在实数集，在实数集范围内数集之间的内在包含关系都是比较明确的，但是对数的发展历程缺乏系统的认知，知识体系还未形成.另一方面,从方程解的角度来看，学生只能在实数集范围内进行求解，缺乏严谨的思维习惯.所以本节课让学生在问题情境中了解数系的扩充过程，体会实际需求与数学内部的矛盾(数的运算规则、方程求根)在数系扩充过程中的作用，感受人类理性思维的作用以及与现实世界的联系.本节课也需要理解复数的基本概念.一方面让学生根据现实生活和数学内部发展需求，体会虚数引入的必要性和合理性．另一方面，让学生体验复数的产生过程，培养学生观察发现问题的能力，引导学生从生活中挖掘数学内容，培养学生的发现意识和应用意识，提高学习数学的兴趣，感受数学的魅力.

2．课例重现

(1)创设情境——形成问题

以卡尔丹的困惑入手：

能否将10分成两部分，且使两者的乘积为40？

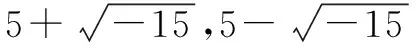
贯穿历史长河，看看数集是如何发展的．

(2)重温“扩充”——分析问题

问题1数系经历了哪几次扩充？

设计意图：帮助学生进行知识梳理，感受由于生活实际需要，数学内部发展都要引入新数，扩充数集．

问题2这几次数系的扩充共同特点是什么？

设计意图：让学生感受到数系扩充的合理性，并能提炼出数系扩充的一般原则：“①引入新数；②在新的数集中，原有的运算及其性质仍然适用，同时解决了某些运算在原来数集中不是总可以实施的矛盾．”为数系的再一次扩充以及如何扩充打好了坚实的基础；同时，有利于培养学生的归纳、概括与表达能力．

历史在前进，社会在发展，生活中的矛盾不断涌现，如何解决卡尔丹的困惑．

(3)引入新元——解决问题

问题2五百多年前摆在数学家面前的困惑如何破解？

引入一个新数i，叫做虚数单位，并规定：

①i2=-1;

②实数可以与i进行四则运算，运算时，原有的加、乘运算律仍然成立.

介绍数学史，让学生了解相关数学发展史，激发学生的学习兴趣.

i是imagination(想象力)的首字母，瑞士数学家和物理学家欧拉(Leonhard Euler1707-1783)在1777年首次提出用i表示平方等于-1的新数，又由德国数学家、物理学家和天文学家高斯(Johann Carl Friedrich Gauss1777—1855)在1801年使之系统的通行于世.

(4)形成扩充——深化问题

问题3①引入新元i后，卡尔丹要找的数是什么呢？

我们把这些含i的数叫做虚数.还能写出其它的数？

②你能写出一个形式把所有的实数和虚数都包含在内吗？

复数的代数形式：通常用字母z表示，即z=a+bi(a,b∈R)其中a是实部，b是虚部，i叫做虚数单位.后面还会学习复数的指数形式，三角形形式.

目前为止，把所有的实数和虚数都放在一起形成新的集合就叫做复数集.

追问：既然复数的代数形式既能表示实数，也能表示虚数，那什么时候表示实数，什么时候表示虚数呢？

设计意图：先用卡尔丹的数引出虚数概念，然后再模仿、尝试写出其他数(包含实数)，引导学生由特殊到一般，从而概括出复数的代数形式a+bi(a,b∈R)，并学习复数的有关概念，从而完成从实数集到复数集的扩充．又根据复数的代数形式再来对复数进行分类，从而深化复数概念，攻克本节课的重点，数系扩充表得以完善．

二、课堂，也要扩充

每一节课，其实就是学生和老师在知识上的扩充，知识的获得是第一层次，学生在课堂上学到了新的内容，扩充了自己的知识层面，教师通过学生的反馈，从教学能力的角度收获也很大.但是知识获取的多少，就要看第二层次，也就是知识的外延和内涵，通过一节课的相关知识，了解知识的前身后世，从点的知识扩充到面的知识，另外通过所学知识能够解决一些新的问题，掌握了一种数学工具.

要想通过本节课学习的知识受益终生，那就要看第三层次，知识的获得方式和效率.本节课首先抛出一个问题——负数开方，在学生已有的实数集上无法解决这个问题，笔者带着学生一起回顾数集发展历史，从原始社会结绳记事、在兽皮上刻横来计数，引入了自然数到欠账，引入了负数，接着度量正方形边长为1的对角线引入了无理数，再到一个苹果四人分，引入了分数……都是根据社会生活实际需要引入了新数，另一边，从数学内部的发展，从运算角度都是有必要扩充数集，加减乘除开奇次方在实数集范围内才能实行.通过这样的引导，让学生重新认识数学课堂，从数学史的角度出发，激发学生的探求欲望，并且能够根据自己的已有知识，体会新数引出的历程，感受数学知识产生的不凡与伟大数学家思考问题的普通.这样的数学课堂才是非常饱满的，学生学习到知识才足够的有价值，课堂的扩充才显性.

三、目标，更需扩充

三维目标是指教育教学过程中应该达到的三个目标维度，即：知识与技能(Knowledge & skills)；过程与方法(Process & steps )；情感态度与价值观(emotional attitude & values).“三维目标”是一个教学目标的三个方面，而不是三个独立的教学目标，它们是统一的不可分割的整体.关于三维目标，新课改方案中已提出多年，但在具体实施的过程中，有些教师总感觉很难把握，还是停留在传统的知识灌输的层次上，不能真正理解三维目标就无法让课堂真正成为学生的伊甸园，无法真正培养社会需要的人才.所以目标的理解是更加紧要的，每一节课都应该有明确的目标，不能只停留在传授学生书本知识，要充分理解三维目标，三位一体只有当真正理解三维目标，才能在教学中贯彻目标的达成度，才能使得初定的目标得到进一步的扩充，从而让学生的知识、思维、能力都得到进一步的扩充.

四、思维，素养的扩充

数系扩充到实数集以后解决不了负数开偶次方，欧拉首次提出i表示平方等于-1的新数，高斯系统地使用这个符号i并且使它通行于世，这样把实数扩充到了复数.这个伟大的扩充解决了负数开偶次方问题，纵观整个扩充过程，如果每一个数学家都能为了解决某一类问题勤于思考，那数学的重大难题会一步一步克服，也能为生活实际解决更多的问题，这样的解决问题的能力和决心，就是需要我们教师每一节课的课堂扩充和目标扩充，拓宽他们的眼界，让学生的思维更加的活跃，从而助力于素养的提高.这样的课堂教学容易激发学生的学习兴趣，树立远大的理想，无形中教育学生要像伟大的数学家一样从细微处着手，从生活实际着手敢于思考，让自己的思维插上翅膀，翱翔天空，让自身的数学素养有一种质的飞跃，从而拓宽数学研究的领域，解决更多的问题，这才是数学教学的真谛.总之，一句话“让他们都有成为数学家的心”.