基于问题导学的高中数学学习活动设计探究——以《直线与平面垂直的判定》为例

杨　蓝

(云南省昆明市第一中学西山学校　650106)

一、问题导学相关概念阐述

所谓问题导学就是以教学内容为基础，精心设计问题情境，引导学生优化学习方式的一种教学过程.在高中立体几何教学中实施问题导学教学模式就是根据所学内容，以教师创设的问题为情境，通过分析学生的“最近发展区”，引导学生形成“问题意识”，在讨论和合作中形成“问题逻辑”，并逐渐在“问题”的导引中实施连续进行的一种教学模式.

二、高中立体几何问题导学教学策略

1.创设有效立体几何问题情境

作为问题导学的成败环节，问题情境要激发学生学习立体几何的动机，一是以某一个知识点为中心，引导学生从不同方向解决与知识相关的问题；二是以旧知识作为铺垫，将新旧知识有机结合起来，使得学生知识以阶梯的方式逐步提高；三是以已有例题为基础，综合其它知识点，或者改变问题方向达到开发思维的目的.在具体问题情境创设中，教师可以采用趣味性数学问题、其它学科知识、猜想与假设、生活实际问题、教具演示、实物与模型、现有教学技术软件等方式创设问题情境.例如，在学习利用空间向量数量积来求二面角大小时，笔者利用学生已经掌握的物理知识，创设了高中物理中力与不在一条直线上的位移所做功的问题情境.

2.有效的“问题串”教学

教师应根据本节课程教学目标、学习主题，重难点知识，设置一些具有层次感、连续性、启发性的问题.例如，在组织学生学习椎体表面积时，笔者设置了以下“问题串”.

问题1.回顾长方形、正方形的表面积，思考它们与展开后的平面图形面积之间的关系.

问题2.按照上述方式，试着在平面上画出棱锥展开后的平面图形.

问题3.类比棱锥，如何根据锥体的几何结构特征，求出它们的表面积？

3.教师灵活“引导”

基本概念、基本定理、解题方法是高中立体几何课程中的核心，教师应抓住这些关键点，引导理论与实际相结合.同时，让学生“学会学习”，充分利用空间向量法、平移法、补形法等技巧型方法，归纳、演绎、类比、抽象、联想等逻辑型思想方法，转化、分类、数形结合等基本数学思想方法.此外，要在学生回答问题后及时给予鼓励和赞赏，要创设出轻松自由、无拘无束的学习环境.

4.灵活把握学生思考时间

“问题导学”并不是提问式教学，许多教师误认为在课堂上学生能够对答如流是良好的学习的现象，其实，这种课堂形式忽视了等待时间的重要性，应充分给予学生思考的时间.对于一些简单考查记忆性的问题，等待时间应控制在3秒左右，对于一些涉及概括性、逻辑推理性的复杂问题，等待时间应长一些，一般以5秒左右为宜，但是并不意味着等待时间越长，教学效果越好.

三、教学实践

仅有相关理论是不够的，高中立体几何问题导学应该是一个实践性很强的教学过程，因此为了研究的深入，笔者以《直线与平面垂直的判定》为例进行深入探讨.

1.温故知新

以学生已经掌握的直线与直线垂直、直线与平面平行、平面与平面平行知识为出发点，以学生所处的教室为例，要求学生寻找出直线与平面垂直关系.

2.创设情境

利用PPT呈现出上海东方明珠广播电视塔图片，并将地面抽象为一个平面，东方明珠塔的中轴线抽象为一条直线，试问如何判断东方明珠塔是否“矗立”在上海浦东这片土地，即东方明珠塔中轴线是否与地面垂直.

3.设计问题“串”

为了得到直线与平面垂直的判定定理，笔者设计了如下“问题串”引导学生探索直线怎么才能与平面垂直.

问题2：已知平面α，a∈α，如果a与平面α内无数直线垂直，则直线a一定与平面α垂直？(思考时间为10s)

4.学生探究

为了使问题更加具体化，笔者通过实物模型设置了如下探究任务：

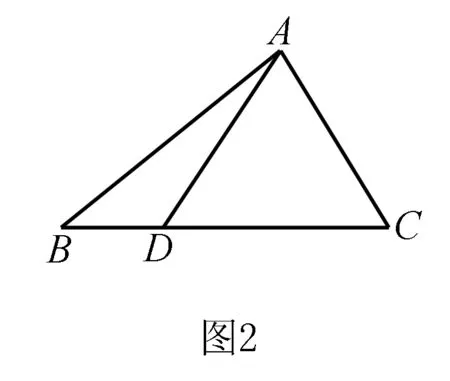
问题3：请学生准备一个如图2所示的三角形纸片，沿着AD方向翻折纸片后将其竖起放在桌子上，试问折痕是否与桌面垂直？(思考时间为5s)

同时，为了引出异面垂直的概念，笔者要求学生进一步思考直线与直线垂直都是相交垂直的吗？(思考时间为5s)

5.揭示规律

为了引导学生自主完成问题，总结出直线与平面垂直判定定理，为探索斜线与平面所成角奠定基础，笔者又设置了以下问题.

问题4：你能否用图形语言表示线面垂直的判定定理？

6.深化知识

在理解直线与平面垂直判定定理后，为了有效巩固这个结论，笔者呈现出了如下问题：

问题7：根据所学知识，自编一道关于“直线与平面垂直的判定”证明题.

综上所述，“问题导学”教学模式充分发挥了教师主导、学生主体作用，促使学生由“学会”变成“会学”.因此，在具体利用“问题导学”教学模式进行授课中，教师应让学生经历数学“再创造”过程，精心酝酿并创设有效的问题情境，引导学生带着问题去学习，并在关键知识点、方法技能、学生情感上加以引导，只有这样才能不断提高高中数学教学的质量.