数学问题解答
2017年12月号问题解答
(解答由问题提供人给出)
2396形如n=16a(16b+15)(a,b∈N)的正整数不能表示成14个整数的四次方和.
(浙江省富阳二中许康华 311400)
证明由x4≡0,1(mod16),得对任意的x1,x2,…,x14∈Z,都有
假设当a=l∈N,∀b∈N结论都成立.
当a=l+1时,如果存在某个b∈N,使得
其中x1,x2,…,x14∈Z,则
所以x1≡x2≡…≡x14≡0(mod2),
这与归纳假设矛盾.
所以当a=l+1时,对一切k∈N,结论都成立.
由数学归纳法知,结论成立.
2397如图,四边形ABCD对角线相交于点O且AO=λOC.记∠ABO=∠1,∠ADO=∠2,∠CBO=∠3,∠CDO=∠4.求证:


(重庆市长寿龙溪中学吴波401249)

而AO=λOC,由此易得S△ABD=λS△CBD.
证毕.
2398设a,b,c>0,a+b+c≤3,求证:
(陕西省咸阳师范学院基础教育课程研究中心安振平712000)
证明记S=(a2+b2+c2+1)(abc).
应用5元算术——几何平均值不等式,得
S2=(a2+b2+c2+1)2(abc)2
(4ab)(4bc)(4ca)
所以S=(a2+b2+c2+1)(abc)≤4.

2399如图,已知⊙O上四点A、B、C、D,BA交CD于E,AC交BD于F,EF交⊙O于H、G,K为EF中点,以点A、K、C作圆交EG于T,求证:HF=TG.

(江西师范高等专科学校王建荣335000,温州私立第一实验学校刘沙西325000)
证明如图,由相交弦定理
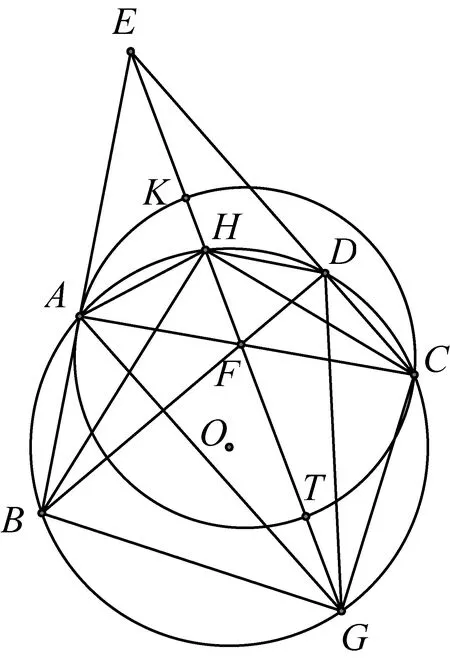
KF·FT=AF·FC=HF·FG
和EF=2KF,因此
HF=TG
⟺KF·FT+KF·TG
=AF·FC+KF·HF
⟺KF(FT+TG)=HF·FG+KF·HF
⟺KF·FG-KF·HF=HF·FG


由面积比可知


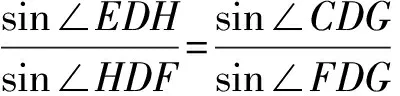

满足三弦共点定理,
2400设△ABC中的三边长分别为a,b,c,外接圆和内切圆半径分别为R,r,求证:
(1)
(河南质量工程职业学院李永利467000)
证明设△ABC的半周长为p,
则a+b+c=2p,abc=4Rrp.
下面分4步进行证明.
(2)
2.由三元均值不等式
(3)
(4)


⟺(a+b+c)3≥27abc

而上式显然成立,故(4)式成立.

(5)
由(2),(3),(4),(5)四式可知(1)式成立.
2018年1月号问题
(来稿请注明出处——编者)
2401在任意△ABC中,求证:

(天津水运高级技工学校黄兆麟300456)
2402在△ABC中,a、b、c、ta、tb、tc,R、r分别表示三边长,内角平分线长,外接圆半径、内切圆半径. 则有
(浙江湖州市双林中学李建潮313012)
2403已知在△ABC中,∠C=150°,O是外心,I是内心,边AC延长线上的点D,边BC延长线上的点E,使得AD=BE=AB,如图所示.求证:
OI⊥DE,且OI=DE.
(北京市陈经纶中学张留杰100020)



试求f(O)+f(H)的所有可能取值.
(河南省辉县市一中贺基军453600)
(安徽省太和县第二小学任迪慧236635)

