2235号问题的推广

刘南山

(江西省都昌县第一中学　 332600)

(1)

该不等式简洁优美、内涵丰富，经探究，可从变元个数和幂指数方面得到如下推广：

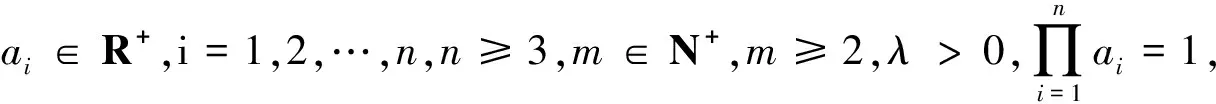
(2)

为证明结论，先给出引理(柯西不等式的变式)：设xi∈R+,yi∈R,i=1,2,…,n(n≥2)，则

该不等式可由柯西不等式直接推出，故证明略.

定理的证明因为m≥2，ai∈R+，i=1，2，…，n， 所以由幂平均不等式得

因为λ>0，所以1+λai>0(i=1,2,…,n)，

由引理和幂平均不等式得

设a1+a2+…+an=x，

所以f(x)在[n,+∞)上单调递增，

故不等式(2)成立，

当且仅当a1=a2=…=an=1时，等号成立，证毕.

问题2235是定理中当n=3,m=2,λ=1时的特殊情形.

显然，在不等式(2)中令n=3,m=2得到：

推论1已知a,b,c是正实数，且abc=1,λ>0,则

(3)

令m=2即得：

(4)

利用类似定理的证明可得：

(5)