涉及三角形边长与半径不等式的简证及加强

安振平

(陕西省咸阳师范学院基础教育课程研究中心　712000)

在文[1]中，笔者提出并证明了如下不等式：

命题1△ABC中，三边长为a,b,c，求证：

①

当且仅当△ABC为正三角形时，等号成立.

通过探究，调整不等式①左面根式内分子字母的次序，获得了如下不等式：

命题2设△ABC的三边长为a,b,c，外接圆和内接圆的半径分别为R,r，求证：

②

当且仅当△ABC为正三角形时，等号成立.

本文先给出不等式②的两个直接证法.事实上

证明1(三角函数方法)记△ABC的面积为S，有

于是，有如下关系式

于是，不等式②等价于

等价于

等价于

③

注意到常见不等式

故③成立，即不等式②获证.

证明2(代数换元方法)由a,b,c为△ABC三边长，可设a=y+z,b=z+x,c=x+y，其中x,y,z为正数．则易知

则不等式②等价于

两边平方，整理知其等价于

因为

所以，只需证

④

这等价于

故④成立，即不等式②获证.

显然不等式④是一个优美的代数不等式，它显然是如下常见不等式的一种有趣组合.

更进一步，通过深入探究，笔者获得了不等式②的一种如下加强.

命题3设△ABC的三边长为a、b、c，外接圆和内接圆的半径分别为R、r，求证：

⑤

证明应用上文的三角函数变形，易知不等式④等价于

等价于

于是，只要证明

等价于较不等式⑤更强的不等式：

命题4在△ABC中，求证：

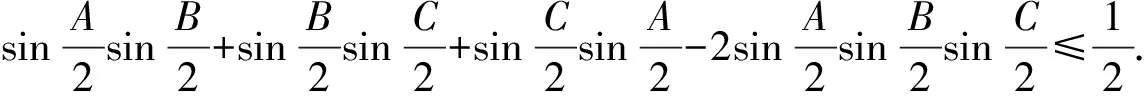
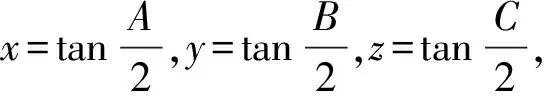
有xy+yz+zx=1,其中x,y,z>0.

于是，不等式⑥等价于

等价于

应用二元均值不等式，得

故(*)成立，即不等式⑥获证.