以信息技术为载体的高考试题
李 艳 徐章韬
(华中师范大学数学与统计学学院 430079)
1 引言
随着科学技术的高速发展,信息技术正悄然地影响着教育,通过对近几年的全国各地的数学高考试题的分析,发现近几年的高考数学题中频繁涉及信息技术,从15年的通信二元码到16年的雷达图运用,再到17年的应用软件,无不彰显着信息技术的影响地位和广泛应用.本文以近三年涉及信息技术的高考数学题为出发点,从分析试题的具体内容到信息技术进入“教学”的类型剖析[1],以信息教育价值为基点,逐层揭示数学教育信息化中构建信息技术与数学知识结合点的策略.
2 内容分析
高考数学题的重点在于对学生的知识及能力的考察,故需要先对题中涉及到的信息技术做具体分析,以及考察内容的重点剖析,发现信息技术与数学知识的结合点,从而为促进教育信息化提供一定的参考.
2.1 通讯二元码——二进制、新定义创新题型
试题1(2015年福建理科卷第15题)一个二元码是由0和1组成的数字串x1x2…xn(n∈N*),其中xk(k=1,2,…,n)称为第k位码元.二元码是通信中常用的码,但在通信过程中有时会发生码元错误(即码元由0变为1,或由1变为0).
已知某种二元码x1x2…x7的码元满足如下校验方程组 :
其中运算⊕定义为:0⊕0=0,0⊕1=1,1⊕0=1,1⊕1=0.
现已知一个这样的二元码在通信过程中仅在第k位发生码元错误后变成了1101101,那么利用上述校验方程组可判定k等于_____________.
信息技术的分析通讯二元码,作为通讯中十分常用的码,与二进制的原理殊途同归,但二元码可以是0、1,也可以是1、2或者其他任意不同的两个值,而二进制就只能是0、1.故二元码不仅具有二进制的特点和原理,还具有二进制不可比拟的优越性,可以是任何两个值的运算,是二进制的一种泛化.二进制作为计算技术中广泛采用的一种数制,当前的计算机系统使用的基本上是二进制系统,数据在计算机中主要是以补码的形式存储的.计算机中的二进制则是一个非常微小的开关,用“开”来表示1,“关”来表示0,因为它只使用0、1两个数字符号,非常简单方便,易于用电子方式实现.
数学知识要点及能力考察新定义创新题型,该新定义运算法则与二进制运算类似,但也有不同之处,其中0⊕0=0,0⊕1=1,1⊕0=1,1⊕1=0,前三个的运算是一致的,但最后一个1⊕1=0,二进制中运算的结果是10,原理是一致,形式不同,实则高考题中常用的伎俩,变相地考察知识点.当然这是考察数学中的一个知识要点,此外,此题最大难点在于逻辑的推理,即学生逻辑推理能力的考察,思维的严谨性,从三个等式中找到错误码元所在,对推理得出的结果进行验证是此题必不可少的步骤,即观察力和思维力的同步进行.
2.2 雷达图——统计类题型
试题2(2016年全国新课标卷第4题)某旅游城市为向游客介绍本地的气温情况,绘制了一年中各月平均最高气温和平均最低气温的雷达图.图中A点表示十月的平均最高气温约为15℃,B点表示四月的平均最低气温约为5℃.下面说法叙述不正确的是()

A.各月的平均最低气温都在0℃以上
B.七月的平均温差比一月的平均温差大
C.三月和十一月的平均最高气温基本相同
D.平均最高气温高于20℃的月份有5个
信息技术的分析雷达图(Radar Chart)又可称为戴布拉图、螂蛛网图(Spider Chart),是财务分析报表的一种.随着计算机的发展,雷达图不仅仅运用于财务报表,而是向多领域推广,再者,雷达图已经不是原始的手工描绘,常见的办公软件等都已经具备了雷达图的自动生成,如Microsoft Office, Kingsoft WPS等,在中间件里有WFsoft wfRadar等不错的应用,在专业的报表图表软件中,则有FineReport等软件,对于多维度数据处理提供了一种新的方向和方法,让统计数据更加直观.
数学知识要点及能力考察数据统计中的一种统计图,常见的统计图有:条形统计图、折线统计图和扇形统计图,这是初中阶段学过的几种主要统计图,随着数理统计的发展,仅仅这三种已经无法满足统计的发展,故新类型的统计图迫切需要被发现和应用,雷达图即是这么一种新型的统计图,多维度的图形统计需要利用雷达图.此题中12个月的气温统计,显然利用折线图也可行,但横轴类型够多,不能集中体现变化趋势,而雷达图就可以解决这类问题,直观感受到气温的变化,集中在圆中的变化:同一圆周上的波动清晰可见.题中告知两点的含义,实则对学生概括能力的考察,根据例子得出图形统计的原理.
2.3 应用软件——等差、等比数列综合题型
试题3(2017年全国I卷第12题)几位大学生响应国家的创业号召,开发了一款应用软件,为激发大家学习数学的兴趣,他们推出了“解数学题获取软件激活码”的活动,这款软件的激活码为下面数学问题的答案:已知数列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16……,其中第一项是20,接下来的两项是20,21,在接下来的三项式20,21,22,依次类推,求满足如下条件的最小整数N:N>100且该数列的前N项和为2的整数幂.那么该款软件的激活码是()
A.440B.330C.220D.110
信息技术的分析应用软件是电脑软件的主要分类之一,是指为针对用户的某种应用目的所撰写的软件.应用软件是为满足用户不同领域、不同问题的应用需求而提供的那部分软件.它可以拓宽计算机系统的应用领域,放大硬件的功能.因应用软件的广泛运用,目前软件开发也成为了热门专业,具有无限丰富和美好的开发前景.
数学知识要点及能力考察等差、等比数列性质及求和公式的综合运用,等比数列的交叉揉合,前N项和为2的整数幂需要满足的条件要进行更进一步地分析才能得到.本题是对抽象概括能力、推理论证能力、运算求解能力、应用意识的考察.本题以应用软件为切入点,通过激活码的设置将软件与数列题型相结合.
当然,除却上述所展示的试题之外,通过研究发现,八年级教材、甚至于更早的高考题中也渗透着信息技术的气息,这说明信息技术早已引起教材的重视,在初中八年级教材中就出现此类题型:信息技术的存储设备常用B,K,M,G等作为存储量的单位.例如,我们常说某计算机的硬盘容量是40G,某移动存储器的容量是64M,某个文件大小是156K等,其中1G=210M,1M=210K,1K=210B(字节).对于一个1.44M的3.5寸软盘,其容量有多少个字节?尽管从表面看就是以信息技术为载体的单位换算,但实际上其中还渗透着二进制的原理,体现了信息技术在教学中的渗透,但如何促进信息技术“进入”教学则是研究的重点所在.
3 信息技术进入试题的类型分析
信息技术 “进入”教学的状况可大致分为 “塞入”、 “加入”、 “嵌入”及“融入”四种类型[2].其不同类型的着重点和性质均不一样,具体关系如下图:

第一层面,“塞入”,即目的是为了使用信息技术而使用信息技术,信息技术与教学内容并无本质的联系,对教学起着“点缀”的作用,其实是可有可无的;第二层面,“加入”,即传统教学无法做到,而信息技术恰好可以帮助解决该问题,可以弥补教学的不足;第三层面,“嵌入”,即为了全面“提升”教学效果,使教学效果整体性地上一个台阶;第四层面,“融入”,也是当前教育信息化研究的重点所在[3],创构出一种与迄今为止截然不同的全新教学时空,旨在使学生在这种全新教学时空中得到尽可能全面的成长与发展.这些是信息技术进入教学的几种形式分类,以此方向来分析前面三道试题,对于试题而言,无论如何也达不到上述的“融入”境界,试题是静态,达不到“融入”层面的动态效果,如试题3,就是非常典型的“塞入”类型,应用软件属于信息技术领域,但实际上应用软件与数列并无实质性联系,知识要点数列根本没有体现出应用软件的某一特点或是原理,可以说这里的“应用软件”只是一种噱头,只能算起着点缀的作用,可能命题者原意就只是为了通过高考题传递这种“教育信息化”的讯息,想让广大一线教师和教育研究者对此引起重视.而雷达图和二元码则是达到了“嵌入”的层面,将信息技术与知识要点巧妙结合,在考察知识要点的同时,让学生了解与其相关的信息技术,如二元码,就是利用二进制与二元码的内在联系,实质无差别的特点,知识、信息同步考察.
4 构建结合点的策略
信息技术只有深入数学学科才能真正发挥其作用[4],结合高考试题中信息化的体现,为实现信息教育价值,故提供构建信息技术与数学学科结合点(即“融入”)的三条策略:深入学科知识、提高信息化水平、明确“价值”追求.
4.1 深入学科知识
构建两者结合点的基础即为深入数学学科知识,充分把握和分析数学学科知识,是真正掌握数学知识的实质所在,亦是构建结合点的必要条件.可以从两个方面来进行分析,一是加深对知识实质性了解;二是发现教学难处所在.正如试题1中的二元码,倘若没有深度地分析和掌握二进制原理,从何谈两者的构建?深入数学学科知识,可以了解到该知识要点讲解的难处,进而为信息技术的结合提供可能.深入学科知识的策略在高考题中也有迹可循:
例1(2001年高考题)如图,小圆圈表示网络的结点,结点之间的连线表示它们有网线相联.连线标注的数字表示该段网络单位时间内可以通过的最大信息量.现从结点A向结点B传递信息,信息可以分开沿不同的路线同时传递,则单位时间内传递的最大信息量为()
A.26 B.24 C.20D.19

此题若简单地进行分析,涉及的知识要点为分类加法计数原理,此种原理的掌握比较容易,但此题从本质上来说是考察“络信息流”——信息的传递,光知晓知识原理是不够的,还需要考虑信息传递的规律和性质,只有对此理解方能解决此题,必须判断每一种类型(路线)中信息量的最大量,也就是我们所说的信息传递的原理.
例2(2003年全国高考数学试题第22题)本题分为两问:
(I)设{an}是集合{2t+2s|0≤s (i)写出这个三角形数表的第四行、第五行各数;(ii)求a100. (II)设{bn}是集合{2r+2t+2s|0≤r 此题表面上看是集合与数列的综合性应用题,从这个方向进行分析和思考无疑增大该题的难度,但若从本质上分析,此题实则考察已学过的知识:二进制,第一问即为二进制数中有两位是1,其余位上均为0,而第二问就是二进制数中有三位是1,其余位上也均为0,1所在的位置决定了数值的大小,将其本质分析到位,那么此题也就迎刃而解.这就是深入学科知识的魅力所在,悄无声息地就将集合、数列两大知识要点与信息技术中的二进制相结合. 例3(2010年北京卷理科20题) 1.证明:∀A,B,C∈Sn,有A-B∈Sn,且d(A-C,B-C)=d(A-B); 2.证明:∀A,B,C∈Sn,d(A,B),d(A,C),d(B,C)三个数中至少有一个是偶数; 此题表面看起来难度十分大,关于集合的综合性难题,很多文章里给了多种方法进行解答,运用“算两次”的解题策略进行解题,而从其本质出发进行分析此题中的第三问实质是二元纠错码码字数的普洛特金(Plotkin)上界[5],将纠错码理论与集合题巧妙结合,将其本质分析透彻则可为解决本题提供方向. 教师,作为教学的引导者,决定着教学的方向,实现教育信息化的前提条件即为提高教师的信息化水平,叶圣陶先生说得好,老师要有一桶水,才能教给学生“一碗水”,要想在课堂上实现信息技术与数学学科知识的结合,首先教师就必须掌握基本的信息素养,没有基本的信息素养,教师即使充分钻研数学学科知识,仍找不到与之相关的信息技术.故教师不仅要求有较高的数学学科知识,而且需要一定的信息化水平,两者缺一不可,因此在师范学校未来教师培训中,必修课可以适当增加信息化课程的比重.传统内容的讲授,也应注意用信息时代的载体表征出来,使之充满时代气息. 所有的“教”都是为了学生的“学”,“教好”的最终目的是“学好”,故要明确两者结合的“价值”追求,简而言之,即结合的目的所在,在上述所参考的分类来看,除了第一类中“为了使用信息技术而使用信息技术,为了应付课程标准”不可取之外,其余三种均可列入考虑之中,“弥补”、“提升”、“创构”均是教学的目标考虑之列,在前两个策略的基础上,发现两者一定的内在联系之后,需要进一步明确结合点的“价值”所在,亦是“目标”所在,这三种没有优劣之分,仅是性质不同,并不是所有的信息技术与学科知识的结合都可以达到“创构”的境界,其中“弥补”和“提升”实则是并驱前行的,两者密不可分,在弥补的同时,亦能促进教学效果的提升.因此,“价值”追求的确定,可以为进一步分析和探究教育信息化提供方向和指南.
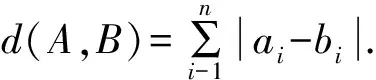
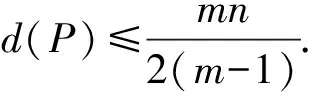
4.2 提高信息化水平
4.3 明确“价值”追求

