具有偏利关系的随机三种群模型的动力学分析

付盈洁,魏春金,张树文

(集美大学理学院，福建 厦门 361021)

0　引言

种群生态学是研究种群数量动态与环境相互作用关系的科学，它是在个体、种群、群落中以种群为研究对象的生态学分支。一般来说，种群间相互作用的关系可以分为竞争、捕食和互惠关系[1-2]。对于一些比较经典的模型，如单种群Logistic增长模型、两种群Lotka-Volterra模型，已经被许多生物学家广泛研究[3-6]，并取得了很好的结果。但是，在现实环境中，捕食者与捕食者之间，捕食者与食饵之间也会出现偏利的情形，如：兰花生长在乔木上，对乔木没有影响，但有利于自己获得阳光和吸收营养。但目前对于偏利关系的三种群模型的研究相对较少[7-8]，文献[8]考虑了如下食饵具有偏利合作关系的捕食-食饵系统：

(1)

其中：x1(t),x2(t),y(t)分别代表种群x1,x2,y在t时刻的密度；ri>0(i=1,2,3)表示种群的内禀增长率；a11>0,a22>0,β>0分别表示种群的密度制约系数；a12>0表示种群x2对种群x1的偏惠系数；k>0表示捕食者的环境容纳量。

文献[8]只对确定性模型进行了研究。但在现实环境中，存在许多随机或偶然的因素影响着生物种群的变化[9-12]，比如：环境噪声会在不同程度上影响增长率、环境容量、竞争系数和系统的其他参数，自然界中任何生物和种群都不可避免地受到外界环境随机因素，人类对环境的破坏，地震、暴雨等自然灾害的影响。因此，本文考虑如下具有第二类功能性反应的随机捕食-食饵模型：

(2)

1　预备知识

L1代表1次函数的空间，1次可积。

设x(t)=(x1(t),x2(t),…,xn(t))(t≥0)是随机微分方程

dx(t)=f(x(t),t)dt+g(x(t),t)dB(t)

(3)

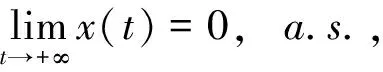
定理2[14](伊藤公式)设x(t)(t≥0)是伊藤过程，其随机微分为dx(t)=f(t)dt+g(t)dBt,

2　主要结论

证明对任意的t>0，作变换:u=lnx,v=lny,w=lnz,则系统(2)变为系统(4)：

(4)

且初始值(u(0),v(0),w(0))=(lnx(0),lny(0),lnz(0))。由于系统(4)满足局部Lipschitz连续，则系统(4)存在唯一局部解(u(t),v(t),w(t)),t∈[0,τe)，其中τe是爆破时间。因此，得到(x(t),y(t),z(t))=(eu(t),ev(t),ew(t)),t∈[0,τe)是系统(2)在初值(x(0),y(0),z(0))条件下的唯一局部解。为了证明这个解是全局的，只需证明τe=+∞。

令k0>0足够大，使得(x(t),y(t),z(t))∈[1/k0,k0]×[1/k0,k0]×[1/k0,k0]，对于任意的正数k≥k0，定义一个停时序列：τk=inf{t∈[0,τe):x(t)∉(1/k,k)，或者y(t)∉(1/k,k),或者z(t)∉(1/k,k)}。

假设τ∞→/ ∞，则存在常数T≥0，∈(0,1)和一个整数k1≥k0，有

P{τk≤T}≥,∀k≥k1

(5)

成立。

设Ωk={τk≤T}(k>k1)，由式(5)可知P(Ωk)≥。则对任意的λ∈Ωk，有x(τk,λ)∉(1/k,k),或y(τk,λ)∉(1/k,k),或z(τk,λ)∉(1/k,k),且V(x(τk),y(τk),z(τk))≥((1/k)-1-ln(1/k))∧(k-1-lnk)。因此，有V(x0,y0,z0)+MT≥E(V(x(τk∧T),y(τk∧T),z(τk∧T)))=E(1Ωk(λ)V(x(τk∧T),y(τk∧T),z(τk∧T)))≥[((1/k)-1-ln(1/k))∧(k-1-lnk)]。其中1Ωk(λ)是Ωk的指标函数。令k→+∞,则有∞>V(x0,y0,z0)+MT=∞导致矛盾，因此必有τ∞=∞，a.s.。

(6)

两边同取极限有

(7)

(8)

同理有

(9)

(10)

-ε2≤y(t)≤ε2。

(11)

将式(8)两边同除以t并移项得

(12)

-ε3≤t-1lnx(0)≤ε3,

(13)

将式(11)和式(13)代入式(12)并放缩得

(14)

-ε4≤x(t)≤ε4,

(15)

将式(10)两边同除以t并移项、放缩得：

(16)

-ε5≤t-1lnz(0)≤ε5,

(17)

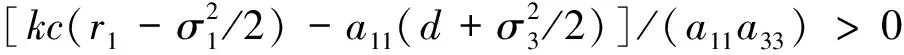
(18)

(19)

(20)

成立。

构造函数V(X)=(1+x*)(x-x*-x*ln(x/x*))+(y-y*-y*ln(y/y*))+(1+x*)(z-z*-z*ln(z/z*)),显然V(X)是正定函数。

由于不等式(cz*(x-x*)2-c(1+x*)(x-x*)(z-z*))/(1+x)≤(cz*(x-x*)2+c(1+x*)|x-x*||z-z*|)/(1+x)≤cz*(x-x*)2+c(1+x*)|x-x*||z-z*|和不等式kc(x-x*)(z-z*)/(1+x)≤kc|x-x*||z-z*|成立，且由杨氏不等式[17]:|x-x*||y-y*|≤[(x-x*)2/(2)+(y-y*)2/2],|x-x*||z-z*|≤[(x-x*)2/(2)+(z-z*)2/2],则有:LV(X)≤-(a11(1+x*)-cz*)(x-x*)2+b(1+x*)[(x-x*)2/(2)+(y-y*)2/2]-a22(y-y*)2-a33(1+x*)(z-z*)2+c(k+(1+x*))[(x-x*)2/(2)+-α(x-x*)2-β(y-y*)2-γ(z-z*)2+δ,其中常数α,β,γ,δ分别为:α=a11(1+x*)-cz*-b(1+x*)/(2)-c(k+(1+x*))/(2),β=a22-b(1+x*)/2,γ=a33(1+x*)-c(k+(1+x*))若δ满足δ

3　数值模拟

为验证结果的正确性，对定理6的结果进行数值模拟。

取r1=1,r2=1,d=0.1,a11=1,a22=0.2,a33=0.5,a=0.3,b=0.5,c=0.5,k=1，并取系统(2)的初始值为(0.4,0.3,0.2)，则有：

由图1,当环境噪声σ1,σ2,σ3都较大时，会使得三种群x(t)、y(t)、z(t)很快地趋于灭绝；由图2，σ2不变，σ1,σ3较小时，种群y(t)趋于灭绝，但是种群x(x),z(t)会持续生存；由图3，σ2,σ3不变，σ1较小时，种群y(t),z(t)趋于灭绝，但是种群x(x)会持续生存；由图4，当σ1,σ2,σ3都很小时，种群x(t),y(t),z(t)相对缓慢减少，并会持续生存。由此可知，随机扰动对种群的生存与灭绝扮演着重要的角色，大的随机扰动会使得种群灭绝。

4　结论

本文讨论了具有偏利关系的随机三种群模型。通过构造适当的Liapunov函数并运用伊藤公式，证明了系统全局正解的存在唯一性、均值有界性，给出了种群灭绝与平均持续生存的充分条件，并证明了平稳分布的存在性。最后通过数值模拟验证结果的正确性，得到以下结论。随机扰动对种群的生存与灭绝扮演着重要的角色，当环境噪声较大时，会使得种群x(t)，y(t)，z(t)更快地趋于灭绝；当噪声强度较小时，种群x(t)，y(t)，z(t)相对缓慢减少，并会持续生存，且在一定条件下，随机模型(2)的任意具有正初值的解(x(t),y(t),z(t))存在平稳分布μ(·)，并且μ(·)具有遍历性。