信息融合与贝叶斯集成的船用中高速发动机磨损故障诊断

王永坚，陈　丹,戴乐阳

(集美大学轮机工程学院，福建 厦门 361021)

0　引言

船用中高速发动机运行转速高,使用环境恶劣，使得发动机运动副经常出现磨损故障[1]。故障的判别与诊断，主要通过监测与发动机运动副磨损紧密关联的运行参数及性能指标等，获得相关的故障征兆信息，通过科学地分析与处理，最后根据故障征兆和其他诊断信息定位并隔离故障，完成故障的判别与诊断。但磨损故障征兆信息往往存在模糊性和不完备性等问题[2]，给船用中高速发动机状态监测和磨损故障诊断带来较大的困难。贝叶斯网络是目前解决模糊性和不完备性问题的有效方法之一，是不确定知识表达和推理领域最有效的理论方法和模型，在故障诊断领域有很大的发展空间[3]。

信息融合技术通过对多个信息源提供的信息合理进行支配，把各信息源在空间或时间上的冗余信息按照某种准则进行组合，以获得对被测对象一致性解释，并产生新的融合结果。发动机磨损故障多源信息融合是指将与发动机磨损相关的故障征兆信息进行融合，以提高磨损故障诊断的精度。

发动机磨损故障多源信息的融合与贝叶斯网络相结合，集成两者的技术优势，能较好地解决船用中高速发动机磨损故障诊断过程中，因故障征兆信息模糊和不完备性带来的故障诊断困难，为发动机磨损故障的准确诊断提供技术支持[4]。

1　船用中高速发动机磨损故障分析

船用中高速发动机由许多部件和运动副组成，是一个复杂的、相互关联的结构系统。不同类型的摩擦副是发动机运动副的物理实现，摩擦副及其润滑控制、状态监测以及补偿控制系统组成发动机摩擦学系统，图1为船用中高速发动机运动摩擦学物理模型。

活塞环侧面与缸套内表面、连杆大端与大端轴承、主轴颈与主轴承、传动齿轮组等是发动机重要的摩擦运动副[5]，通过获取与磨损故障相关的故障征兆信息，并将这些信息进行科学的分类、融合，从而判别运动副的磨损状态[6]。

2　船用中高速发动机磨损故障贝叶斯诊断网络

2.1　贝叶斯网络

贝叶斯网络(bayesian networks)又称为信念网络[7]，是一种基于网络结构的有向无环图解概率模型(DAG模型)，使用条件概率表示其量化关系，用一个二元组B(G，P)表示一个贝叶斯网络，其中：G表示有向无环图；P表示条件概率表。

根据贝叶斯网络基本原理，将与磨损故障诊断有关的各种信息(如故障征兆、故障模式等)用节点形式表示，节点之间的关联关系用网络中的有向边连接，紧密程度则通过节点间的条件概率(CPT)进行表达。将贝叶斯网络应用于发动机运动副的故障诊断，不仅能够有效地处理故障诊断过程中不确定问题，还能对多源异类信息进行有效表达与融合[8]。

2.2　发动机磨损故障贝叶斯诊断网络

发动机磨损故障诊断一般从运动副发生磨损故障时出现与之关联的典型故障征兆信息出发，挖掘运动副出现磨损故障时呈现的故障征兆与故障模式(如缸套擦伤等)之间的因果关系，最终获得故障原因和故障位置。笔者获取了近几年合作单位受控船舶中高速柴油机发生磨损故障时的大量监测信息，并邀请相关领域专家对以上数据进行归类、分析与评判，确定了发动机典型磨损故障征兆及故障模式层次表，如表1所示。

表1　船用中高速发动机磨损故障层次表

1)发动机贝叶斯诊断网络结构的搭建。为降低贝叶斯网络建构的复杂性，在网络建构过程中，运用朴素贝叶斯分类器(NB)原理，即：网络结构为两层贝叶斯网路，包含一个类变量父节点，其余为属性变量子节点，各属性变量节点Si相互类条件独立，每个属性节点Si只与类节点F相关联。根据表1确定发动机磨损故障典型征兆节点与故障模式节点的对应关系，搭建发动机贝叶斯诊断网络结构，如图2所示。

2)网络参数的学习。发动机磨损故障贝叶斯诊断网络结构中各故障征兆节点条件概率的学习和确定，有两种方式：一是在缺乏足够故障训练样本情况下，通过询问领域专家获取相关数据信息，采用概率刻度法进行赋值[3]；二是具有完整数据的贝叶斯网络进行参数学习[9]。学习的目标是根据概率分布的先验分布和训练样本数据计算的后验概率分布。设概率分布向量θij=(θij1,θij2,…,θijai)，在θij相互独立的情况下，若无数据缺失，则后验概率分布保持独立，且有：

(1)

式中：D为训练样本集；S为网络结构模型；θs为概率分布向量。

取Dirichlet分布p(S4/F,S3)，作为先验分布，结合磨损故障征兆训练样本数据，可得后验概率分布为：

θijk=(αijk+Nijk)/(αij+Nij)。

(2)

3　多源信息融合发动机磨损故障贝叶斯诊断

3.1　贝叶斯参数估计的多源故障征兆信息融合

设船用中高速发动机在某一持续运转时间内被测样本有m个故障模式，Fj={F1,F2,…，Fm}，n个与故障模式相关联的征兆信息为S={S1,S2,…，Sn}，故障征兆信息的测量模型[6]：

S=f(Fj)+υ。

(3)

式中：f(Fj)为S与Fj的函数关系；υ为随机噪声。

单个磨损故障征兆的估计计算过程：

(4)

式中：P(Si)为故障征兆测量数据的分布概率；P=Fj/Si为磨损故障模式Fj的后验概率。

2)取风险最小的估计准则，必须使：

(5)

则单个磨损故障征兆信息的最大后验概率最优估计值为：

(6)

同理，在发动机磨损故障诊断系统中，加入n-1个与磨损故障模式相关的故障征兆信息后，最大的后验概率估计的算法与单个故障征兆信息时是一致的，此时，n个故障征兆信息的融合值为：

(7)

这样，发动机磨损故障状态的多源故障征兆信息的融合问题就可以通过寻找故障模式Fj的后验概率P=Fj/Si获得解决，并获取相应的最大后验概率估计值。

3.2　故障模式贝叶斯分类器设计

当发动机磨损故障多源故障征兆信息融合后，根据贝叶斯定理，设定故障征兆信息S={S1,S2,…,Sn}，则磨损故障模式Fj的概率为：

P(Fj/S1,S2,…,Sn)=P(S1,S2,…,Sn/Fj)P(Fj)/P(S1,S2,…,Sn)=αP(S1,S2,…,Sn/Fj)P(Fj)。

(8)

式中：α为正规则化因子α=1/P(S1,S2,…,Sn)；P(Fj)为类Fj的先验概率。

式(8)还可表示为：

(9)

将式(9)带入式(7)得到：

(10)

采用NB分类器后，式(10)又可表示为：

(11)

通过式(11)可以计算出磨损故障模式Fj的最大后验估计值，从而给出最可能的发动机磨损故障模式。

3.3　发动机磨损故障贝叶斯诊断过程的实现

运用贝叶斯参数估计算法，将与发动机磨损故障相关的各种故障征兆信息(参见表1)进行有效融合，增加信息的完备性，为故障的正确诊断提供可靠的证据信息。图3为发动机磨损故障贝叶斯诊断流程图。诊断过程如下：1)通过采集受控船舶中高速柴油发动机部分机组发生磨损故障时各种故障征兆信息，并根据发动机说明书规定的运行和性能参数的使用警告值、领域专家的经验建议以及行业推荐的使用范围标准等，对已采集的故障征兆信息进行典型特征信息的提取；2)利用贝叶斯参数估计算法，对发动机磨损典型故障征兆信息进行多特征信息融合；3)综合利用已获取的大量与发动机磨损故障相关的故障征兆训练样本，结合领域专家丰富的故障诊断经验知识，运用贝叶斯网络方法构建故障征兆信息与故障模式之的联系，搭建发动机磨损故障贝叶斯诊断网络结构；4)通过建立朴素贝叶斯分类器，消除故障征兆信息模糊性影响，并简化信息融合结果；5)通过最大后验概率估计值的比较获得诊断结论。

4　验证分析

发动机磨损故障征兆样本数据均来至合作单位受控船舶中高速发动机，选取475组数据作为发动机磨损故障试验样本，开展计算分析。各故障模式训练与测试样本如表2所示。

以一台受控发电柴油机(潍柴6170，转速1 000 r/min，额定功率300 kW，曲轴箱润滑油使用时间为5 882 h)的磨损故障为测试样本，故障模式为F32(大端轴瓦表面材料剥落)，将获取的现场及送检曲轴箱润滑油理化/铁谱/光谱检测的典型征兆信息与正常使用范围进行对比，如表3所示。该测试样本故障征兆状态为{0,0,0,1,1,0,1,1,1,1,1,0}，结合诊断网络模型条件概率学习原理，根据图1，可获得如表4所示各故障模式条件概率值。

表2　故障样本分配表

表3　某受控柴油发动机5 882 h时间段磨损故障征兆对比数据

表4　受控柴油发动机某次故障征兆各故障模式条件概率一览表

磨损故障诊断过程如下：

由式(9)可得：

P(Fj/S1,S2,…,Sn)=αP(Fj)·(P(S1|Fj)·…·(P(S12|Fj)。

(12)

表5　受控柴油发动机某次故障征兆各故障模式先验及后验概率一览表

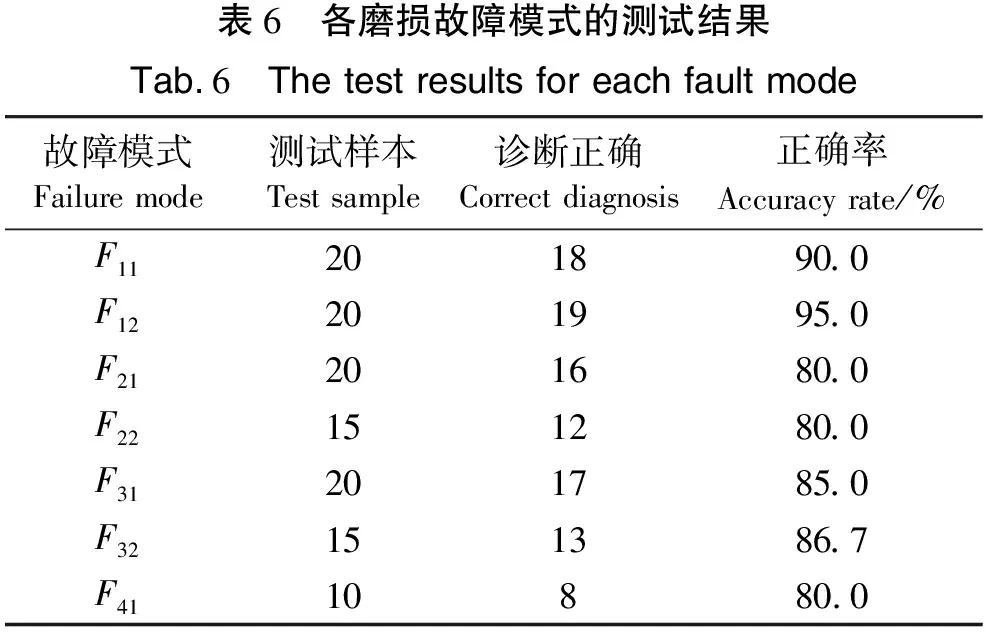
表6　各磨损故障模式的测试结果Tab.6　The test results for each fault mode故障模式Failure mode测试样本Test sample诊断正确Correct diagnosis正确率Accuracy rate/% F11201890.0F12201995.0F21201680.0F22151280.0F31201785.0F32151386.7F4110880.0

5　结束语

1)为准确诊断船用中高速发动机磨损故障问题，提出了多源故障征兆信息融合技术与贝叶斯网络相结合的故障诊断方法，通过受控柴油发动机实际数据测试，证明了该方法是可行的。

2)提出了基于贝叶斯参数估计算法的多源特征参数的融合方法；搭建发动机磨损故障贝叶斯网络模型；建立发动机磨损故障朴素贝叶斯分类器，消除故障征兆信息模糊性的影响，并简化信息融合结果。

3)本文提出的发动机磨损故障诊断方法是有效的，所建网络模型是准确的，为快速、准确诊断发动机磨损故障问题提供了技术支持。