基于VSTF离散化的O-OFDM系统预补偿

梁　猛,王怡雯

(西安邮电大学 电子工程学院， 陕西 西安 710121)

光正交频分复用(optical orthogonal frequency division multiplexing，O-OFDM)技术是目前光纤通信研究领域的热点，具有抗多径衰落、抗色散的性能[1]。但是，光纤的非线性效应依旧是目前影响光通信质量的一个重要因素。

非线性薛定谔方程(nonlinear Schödinger equation，NLSE)用来描述光脉冲在光纤中的传播过程，和线性衰减、色散以及各种非线性效应[2]。理想单模光纤信道中基于沃尔泰拉级数传递函数(Volterra series transfer function，VSTF)的NLSE的半封闭式解析解[3-4]，可以用于研究色散、非线性效应对光脉冲的传输影响。利用基于稀疏沃尔泰拉矩阵在接收端设计非线性均衡器，对O-OFDM系统中的非线性进行电域的均衡[5],或基于逆VSTF的非线性电域补偿方法[6]，在偏振复用级联放大系统中有良好的补偿效果。

然而，接收端的均衡在补偿非线性的同时会放信道中的噪声，且连续的VSTF形式复杂度高，不便于计算。因此，考虑使用VSTF离散化的处理方法，降低原有VSTF表达式的复杂度，在O-OFDM系统发送端实现离散化p阶逆VSTF预补偿算法。

1　VSTF基本理论

1.1　基于沃尔泰拉级数的NLSE的解

非线性薛定谔方程描述了光脉冲在光纤中传输演化的过程。由于考虑所有光纤效应时非线性薛定谔方程不能解析求解[7]，因此对非线性薛定谔方程进行简化。在只考虑线性衰减、二阶色散，各种非线性效应综合在一起的情况下，非线性薛定谔方程可以表示为[8]

(1)

其中，A=A(t,z)是光信号的电域包络，t为传输时间，z为传输距离，β2是二阶色散系数，α是光纤的线性衰减，γ是光纤的非线性系数。

对式(1)做傅里叶变换得到频域的非线性薛定谔方程，并求解偏微分方程得到沃尔泰拉级数一阶及三阶核函数[6]

(2)

则VSTF可表示为

(3)

其中,A(ω,z)是A(t,z)的傅里叶变换，A*(ω,z)为A(ω,z)的共轭。式(3)是光脉冲在光纤输入端的频域形式，ω是输入光频率，ω1和ω2是参数的虚拟变量，并在不同频率影响光波之间的交互作用，尤其是信道之间的相互作用。因光纤中不存在偶数阶非线性效应[9]，故式(2)中没有偶数阶核函数。

如果要求更高的计算精度，那么可以计算更高阶的核函数，五阶甚至七阶核函数，该算法已被证明收敛[10]。

1.2　沃尔泰拉级数的p阶逆

图1是沃尔泰拉级数的p阶逆模型[11]。对于给定的非线性系统H，其p阶逆为Kp，S(t)为p阶逆输出。

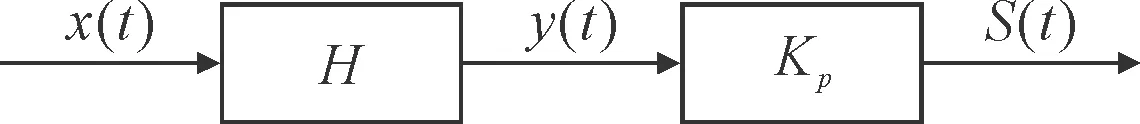
图1沃尔泰拉级数的p阶逆模型

根据p阶逆理论[12]，沃尔泰拉级数的p阶逆模型可由VSTF核函数给出[13],即

(4)

其中，L与z均为光纤传输距离。则经过p阶逆后的输出可以表示为

(5)

这是光脉冲在光纤中传输了距离L后的输出。以沃尔泰拉级数的p阶逆表达式设计非线性均衡器，既能用作预补偿，又能用作后补偿[14]。用作预补偿时以正向输出作为均衡器的输入，这样就能得到补偿后的输出。

2　O-OFDM系统VSTF离散化

一个OFDM符号内包含N个经过相移键控或正交幅度调制(quadrature amplitude modulation，QAM)的子载波，其数学表达式为[15]

(6)

其中，rect(t)是矩形函数，即

N表示子载波的个数,T表示OFDM符号的宽度,dk为分配给每个子信道的经过调制的信息符号(包括时域信息和频域信息),fk表示第k个子载波的频率。O-OFDM系统具体结构如图2所示。

由于VSTF是在频域描述输入与输出关系的函数，而OFDM信号在经过快速傅里叶逆变换(inverse fast Fourier transform，IFFT)之后变为时域信号。若要利用VSTF处理OFDM信号，就需要找出OFDM信号的频域信息。OFDM频域信号就是QAM调制之后IFFT变换之前的信号。提取出进行IFFT之前的信号的频域信息，进行VSTF变换。

图2　O-OFDM系统结构

根据式(6)分析可知，dk所携带的频域信息就是进行IFFT之前，QAM调制之后的信号携带的频域信息，此时的频域信息都是离散的。因此对频域连续的VSTF进行离散化处理，得到离散化VSTF表达式为

(7)

离散化p阶逆VSTF表达式为

经过离散化，原本复杂的二重积分变为求高斯和，降低了计算复杂度。

3　算法仿真验证与分析

根据离散化VSTF算法在O-OFDM系统中加入预补偿模块，并且光纤链路中不添加色散补偿光纤，对非线性效应也不做其他任何处理，结构如图3所示。

图3　带预补偿模块的O-OFDM结构

根据预补偿算法进行仿真。其中，中心频率

ω0≈200 THz，

线性衰减系数

α=0.2 dB/km，

二阶色散参数

β2=16.8 ps/(nm·km)，

非线性系数

γ=0.001 4 m-1W-1,

光纤传输距离

z=L=100 km。

输入脉冲为经过OFDM调制的离散频率信息，子载波数为64。为简化问题并使问题具有针对性，系统中未做其他色散和非线性的补偿处理。在信道中加入使信噪比为25的高斯白噪声后的星座图如图4 所示。预补偿前后,系统误码率随传输距离的变化曲线如图5所示。

图4　接收端星座图

从图4可见，在添加了VSTF预补偿模块后，星座图从补偿前的杂乱无章变为规律排列。图5中系统误码率从补偿前的46.20%降到了补偿后的0.21%，可见离散化VSTF预补偿算法对光纤信道中的色散及非线性效应有良好的补偿效果。

图5　系统误码率随距离变化传输曲线

4　结语

针对光正交频分复用系统受色散及非线性效应影响较大的缺点，通过将沃尔泰拉级数传递函数进行离散化处理的方法，降低原有VSTF复杂度，并将其应用于O-OFDM系统发射端，实现了O-OFDM系统的离散化VSTF的p阶逆预补偿算法。通过数值仿真计算，补偿后星座图较补偿前变化明显，分布更为规律，系统误码率明显降低，说明所给算法对O-OFDM系统中的色散和非线性效应有良好的补偿效果。