基于CNN高维超混沌系统图像加密算法

张　琴,林　达,余　亮

(1.四川理工学院 自动化与信息工程学院， 四川 自贡 643000；　2.四川理工学院 物理与电子工程学院， 四川 自贡 643000)

随着通信技术的快速发展和普及，多媒体通信已成为一种重要的通信手段，并为人们的工作和生活提供了极大的便利。与此同时，信息传递的安全性正变得越来越重要。图像作为信息传播的重要载体之一，而图像加密是保证图像信息安全的重要手段。因此，图像加密及解密算法和技术已经成为信息安全领域中的重要问题之一。

图像通常是以二维矩阵的形式存储，用传统的加密算法如数据加密标准(Data Encryption Standard，DES)、高级数据加密标准(advanced encryption standard，AES)、非对称加密算法(RSA)等加密图像，则需将待加密的图像重新排列成明文的形式，这样会导致加密时间长，加密效率不高等缺陷[1]。另一方面，由于混沌系统所产生的信号具有确定性，类似噪声的统计特性与非周期性，且对初始条件极端敏感性等，可应用于图像加密，并且能够表现出许多优良的密码学特性[2]。因此，混沌密码学在图像加密上的研究引起了众多学者的关注。

细胞神经网络[3-4](cellular neural network，CNN)是一种非线性动力混沌系统，是基于Hopfield神经网络和细胞自动机的一种人工神经网络[3]，具有复杂的混沌动力学特性，同时具备实时、高速、并行处理信号等特点，且易于实现超大规模集成电路。因此，CNN系统被广泛用于加密系统[3,5]，并在彩色数字水印加密[6]、语音加密[7]和图像加密系统[2]中均取得了良好的加密效果。目前，文献基于混沌系统的图像加密算法主要有离散混沌系统的图像加密[8]、连续混沌系统的图像加密[9]和混合混沌系统的图像加密[10]等3种。

为了进一步提高图像加密算法的保密性，获得更大的密钥空间及更好的不可预测性，本文提出一种基于高维CNN的超混沌系统的图像加密算法。先通过研究一种高维CNN的超混沌系统动力学特征，然后，依据其特征设计并生成伪随机序列算法，再利用所生成的伪随机序列算法，通过治乱和扩散等方法，完成对图像的加密。最后，通过仿真验证算法的有效性，测试了算法的安全性和鲁棒性。

1　细胞神经网络超混沌系统

考虑一种超混沌系统模型[3]

(1)

其中

b、c、d、e分别为系统的控制参数。当控制参数

a=2，b=11，c=12，d=2，e=101

时，系统式(1)呈现为超混沌状态。

采用四阶龙格库塔离散算法，对系统方程(1)进行迭代，得到混沌时间序列图及吸引子相图如图1 所示。图1仅列出部分时间序列图及吸引子相图，其他时间序列图及吸引子相图类似。从图1可知，该混沌系统呈现特定吸引域的遍历性，可以生成复杂随机且不可预测的信号。

(a) x1时间序列

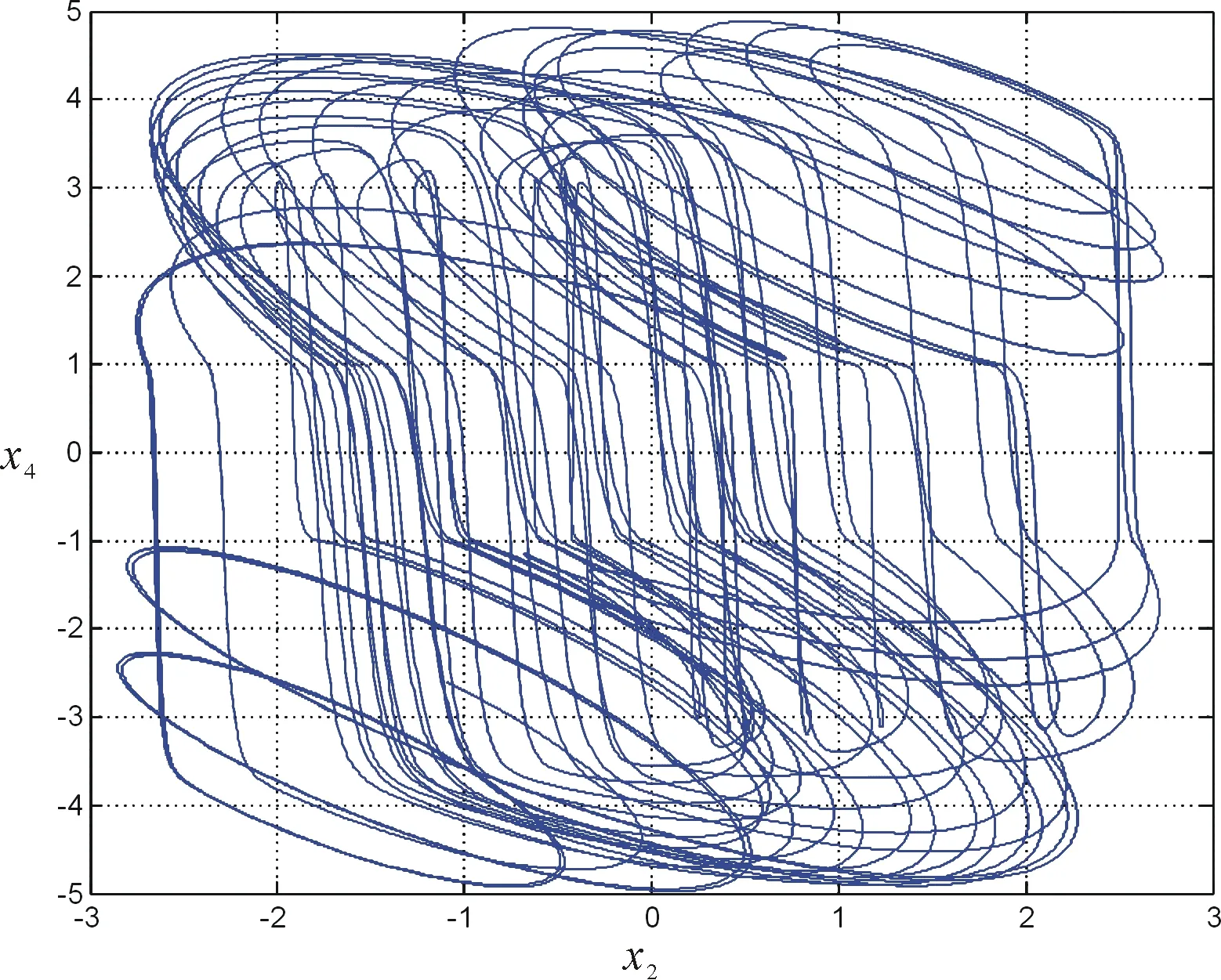
(b) x2-x4平面

(c) x1-x4-x5三维吸引子

(d) x2-x3-x5三维吸引子

该5阶CNN超混沌系统具有3个特点:(1)该系统结构较低维系统更为复杂，生成的信号具有不可预测性；(2)该系统较低维系统具有更多的系统参数和初始值，具有较大的密钥空间；(3)该系统可产生多路混沌序列，应用于图像加密中更为灵活。

2　伪随机序列发生器设计算法

2.1　伪随机序列发生器的设计

图像加密与传统的流密码加密类似。流密码的长度取决于待加密图像像素的大小，图像像素越小，流密码长度越短，反之，图像越大，流密码长度越长。对于灰度图像而言，假设图片为M×N的矩阵，则至少需要生成长度为M×N的密钥流。密钥流由混沌序列组成，因此，减少图像加密时间的一个重要方法就是减少混沌序列的长度。为了充分利用混沌序列，故本文采用多路混沌序列生成密钥流，伪随机序列发生器的结构框图见图2。

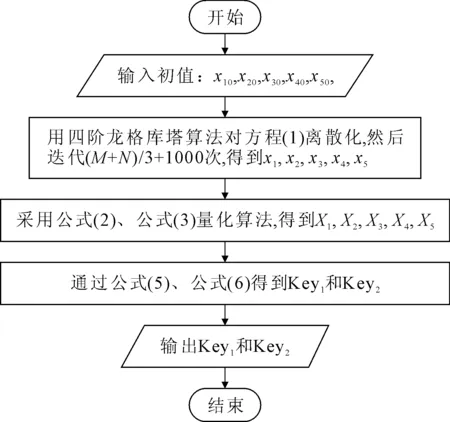
图2　伪随机序列发生器的结构框图

2.2　伪随机序列生成算法

假定灰度图像的像素大小为M×N，具体的伪随机序列生成为算法可以按照如下3个步骤完成。

(1)生成超混沌序列

任取初始值(x10,x20,x30,x40,x50)代入CNN超混沌系统方程(1)中，迭代(M×N)/3+1000次。如果图像像素大小M×N不能被3整除时，迭代次数应保证所产生的序列长度不得少于图像像素的大小。为了消除混沌序列暂态效应以及提高对初始条件的敏感性，采用丢掉混沌序列前1000组的值后，每次迭代所得到序列记为x1j,x2j,x3j,x4j,x5j(其中，j=1,2,…,(M×N)/3，表示每一维的长度。)，即为所生成的超混沌序列。

(2)超混沌序列量化

对超混沌序列进行量化，采用方式为

Δxij=xij- └xij┘,

(2)

得到超混沌序列的小数部分。式中 └xij┘表示取小于或等于xij的最近整数。i=1,2,3,4,5,表示系统的维数。再来量化小数部分，利用方程

Xij=mod( └Δxij×1014┘,256),

(3)

其中，Xij表示系统第i维第j个量化值。i=1,2,3,4,5,表示系统的维数，j=1,2,…,M×N÷3，表示系统每一维的长度，最终得到整数序列{X1j,X2j,X3j,X4j,X5j}.

(3)生成密钥流

将每个整数序列Xij表示为8位2进制。利用

可得

bi,j,u= └Xij/2u┘ mod 2,

(4)

式中u=0,1,…,7。即可得到Xij的二进制表述。对应二进制的组合分别得到伪随机序列Key1和Key2，即为所需的密钥流，其表示式分别为

(5)

(6)

其中，j=1,2,…,(M×N)/3，j和k的关系表示为

k=3j-2。

按照上述步骤，可以得到伪随机序列密钥流Key1和Key2，即可用Key1和Key2对图像进行加密。对于加密图像而言，伪随机序列生成方法决定了混沌系统产生混沌序列的长度。考虑到混沌序列长度为(M×N)/3，加密图像的大小为M×N的灰度图像。对于5维微分方程，我们使用4阶龙格库塔法生成混沌序列值。

3　灰度图像加密和解密算法

3.1　灰度图像加密算法

在文中第一部分可知，当控制参数分别取值

a=2，b=11，c=12，d=2，e=101

时，由超混沌系统方程(1)生成混沌序列，然后应用第二部分所提出伪随机序列发生器产生加密图像时所需的密钥流。具体的加密算法如下。

(1)像素置乱算法

像素置乱阶段是一个像素从一个位置到另一个位置的过程。该过程必须是一一对应关系，以便能够再次恢复图像而不会产生失真[11]。置乱阶段可以用一个矩阵来表示，每个矩阵元素为原始像素位置所对应新的位置。假定置乱矩阵为T，其矩阵元素Tij，且为M×N阶，与图像大小相一致，图像像素位置是从左上角到右下角进行置乱的。

利用伪随机序列构造置乱矩阵，再将图像明文矩阵P进行像素置乱，得到图像密文矩阵C1。像素置乱方式为

(7)

其中clnew，rwnew分别表示图像密文矩阵C1的行和列的下标。

像素位置置乱后得到密文图像C1。仅使用置乱算法进行图像加密，安全性还不够高，被破译的可能性会很大。为了提高算法的安全性，将对C1采用分别进行横向和纵向扩散。

(2)像素值横向扩散

对密文图像矩阵C1进行横向扩散，横向扩散的过程如图3(a)，方法是利用密钥key1对C1进行扩散得到密文图像C2，具体对应的横向扩散方程为

(8)

式中C1(i,j)和C2(i,j)分别表示矩阵C1和C2的矩阵元素。

(3)像素值纵向扩散

像素值纵向扩散是对所得到密文图像矩阵C2再进行纵向列扩散，纵向扩散的过程如图3(b)。方法是利用key2对C2进行纵向扩散，得到最终密文图像C，纵向扩散方程为

(9)

式中C(i,j)表示矩阵C的矩阵元素，即完成灰度图像加密算法。

(a) 横向扩散过程

(b) 纵向扩散过程

3.2　灰度图像加密算法

按照上述步骤即可完成图像加密，而对应的解密的过程则是加密的逆过程。解密是否可逆的关键是所设计的置乱矩阵是可逆矩阵。由实验数据得知，本文所采用256×256阶置乱矩阵为非奇异矩阵，其行列式不等于零，故其具有可逆性，使用的解密密钥也是加密过程中所用的密钥。因此，本文所提的解密算法是可行的。鉴于解密过程是加密过程的逆过程，不再赘述。

4　实验结果及安全性分析

4.1　实验结果

实验中，混沌系统参数分别设为

a=2,b=11,c=12,d=2,e=101，

利用matlab模拟加密解密算法。机器配置为4G的内存，2.6GHz CPU。以256×256灰度图像plane为例，系统方程式(1)初始值取[-1,0.2,0.8,0,1.5]，图像加密及解密结果分别如图4所示。

图4加密解密图

4.2　安全性分析

4.2.1密钥敏感性分析

如果加密方案对密钥敏感，则密钥的微小变化将会引起密文的很大不同，密钥发生微小变化将导致了解密失败。密钥的微小改变采用原始加密密钥与对应微小变化的加密密钥组成的密钥对方式，来测试加密系统对密钥的敏感性。如表1是采用不同的5个秘钥对时，本文算法所相应的平均变化强度和像素个数改变率测试结果。从表1可见，平均变化强度和像素个数改变率的结果分别为33%和99.6%，因此，本文所提出算法的加密系统对密钥具有较强的敏感性，符合加密安全要求。

表1　密钥敏感性测试结果

4.2.2密钥空间分析

对于超混沌系统，密钥空间的大小一般取决于超混沌方程的初始值及系统的控制参数。本文CNN超混沌系统有5个初始值，5个控制参数，因此，密钥空间为1014×10，远远大于理论要求值2128。

4.2.3抵抗差分攻击分析

攻击者通过观察明文微小变化引起解密的变化，找到图像明文与图像密文的相关性。如果原图像的微小变化能引起密文的很大变化，差分攻击的影响会减小。抵抗差分攻击的指标采用像素个数改变率(Number of Pixel of Change Rate，NPCR)和平均变化强度(Unified Average Changing Intensity，UACI)。像素个数改变率是通过评估两图像像素不同的数目来获得两图像的差异，其定义[12]为

(10)

其中D(i,j)是两幅加密图像I1和I2对应像素差异值，其取值为：如果I1(i,j)≠I2(i,j)，则D(i,j)=1；如果I1(i,j)=I2(i,j)，则D(i,j)=0；M和N为图像的宽和高。平均变化强度是通过评价视觉效果的变化来获得两图像的差异，其定义为

(11)

明纹改变1比特，本文算法像素个数改变率和平均变化强度本算法测试结果如表2。可以看出，NPCR值接近理论值0.99，UACI值接近理论值0.33，说明本文加密系统对明文具有好的敏感性。

表2　明文敏感性测试结果

4.2.4相关性分析

相邻像素的强相关性是图像的一个重要特征，一般用相邻像素相关性来恢复原图像，如果通过相邻像素不能获得加密图像的像素，则认为加密算法是有效的。本文算法明文图像与密文图像的像素分布图如图5所示。图5(a)～5(c)为明文相邻像素相关性分布图，图5(d)～5(f)为密文相邻像素相关性分布图。从图可见，加密图像的像素是杂乱无章的，无规律可寻，因此，通过相邻像素相关性来复原加密图像是几乎不可行的，说明加密算法是有效的。

图5　明文与密文相邻像素相关性分布图

4.2.5信息熵分析

信息熵是衡量随机系统复杂度的一个指标，计算公式[1]为

(12)

式中H(S)表示信息熵,P(Si)表示每一级灰度值出现的概率。一般情况，如果图像像素值用8比特位表示，当图像处于理想的混沌状态时，信息熵的值为8。本文算法选取的灰度图像大小为256×256，其加密图的信息熵为7.9668，大于文献[13]中的加密图信息熵(7.69)，说明本文算法较文献[13]具有更多的复杂性。

4.2.6特征统计攻击分析

为了防止攻击者获得图像的特征像素，统计分析是图像加密算法需要考虑的一个因素，图6(a)为明文直方图，图6(b)为密文直方图，从图中可见，加密图像具有统一分布均匀性，对于攻击者而言，是不容易破解的。

图6　明文与密文直方图分布图

4.2.7鲁棒性分析

鲁棒性指加密图像在传输过程中受到攻击或噪声污染时，对原图像进行解密的能力[14]。我们选取常见的椒盐噪声作为污染源，分析其污染加密图像时，加密图像的鲁棒性。图7分别表示噪声污染等级Δ=0.1和Δ=0.01为时，本文算法的测试结果。从结果可以看出，等级的椒盐噪声的污染，解密算法仍然能够将加密图像恢复成原图像。此外，对本文算法进行了剪切攻击测试，其结果如图8。图8(a)为将加密的图像剪切掉一个小三角形后，经过本文解密算法，图8(b)为原图恢复解密图像。可见，剪切后的加密图像，经过解密后，仍然能够恢复成原始图像。因此，本文提出的算法具有好的鲁棒性。

图7　加不同等级的椒盐噪声的解密图像

图8　剪切攻击后的解密图像

5　算法比较

为了说明本文算法的优点，本部分将吧本文所提出的加密算法与其他相关文献所提出的研究结果进行对比。首先，将本文算法的NPCR和UACI的值与其他相关文献进行对比，结果见表3。可见，本文算法的NPCR和UACI的值均高于文献[15-17]的值，并且与理论值相一致。其次，将本文算法的相关系数与其他相关参考文献进行对比，其结果见表4。可以看出，文献[18]水平方向系数是最低的，本文算法的垂直方向系数及对角线方向系数是最低的。因此，本文算法较其他文献的算法相比具有较好的性能，更能够抵抗任何攻击，适合图像加密。

表3　本文算法与其他文献的NPCR与UACI对比

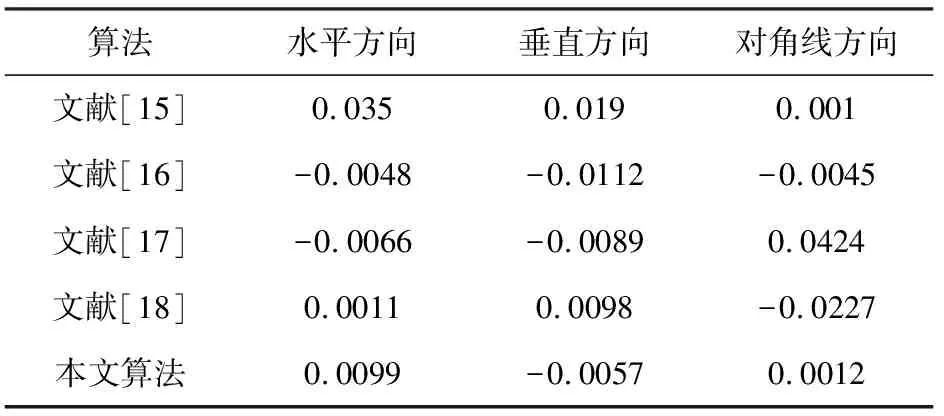
表4　本文算法与其他文献的相关系数对比

6　结语

基于一种五维CNN超混沌细胞神经网络系统提出一种混沌序列生成算法，充分利用了系统混沌序列特点生成密钥流，极大地减少了混沌序列的长度，在扩散过程中利用密钥流，并利用置乱和扩散方法，实现灰度图像的加密和解密。通过仿真方法证明了算法的可行性，安全性分析结果表明，本文算法具有较强的复杂性、安全性和鲁棒性。与相关算法的比较结果表明，本文算法较已有的算法具有较高的平均变化强度和像素个数改变率，在扩散阶段及置乱阶段具有一定的优势。因此，是一种性能较好的图像加密算法。