一种OFDM联合峰均比抑制算法

李　波,郑　晨,王彦本

(西安邮电大学 通信与信息工程学院,陕西 西安 710121)

正交频分复用(orthogonal frequency division multiplexing,OFDM)采用相互正交的子载波传输信号，能够提高数据传输速率，抵抗无线信道多径传输带来的频率选择性衰落[1]。自20世纪50年代出现至今，OFDM技术广泛应用于高比特率数字用户线系统，数字音频广播系统和长期演进等系统中[2]。

信号的高峰均功率比(peak to average power ratio,PAPR)是OFDM技术应用所面临的难题之一。当多个子载波上的信号出现同相叠加时，会产生超出大功率放大器(high power amplifier,HPA)线性工作范围的尖峰信号，引起信号的畸变和频谱的扩散。现有的主流的峰均比抑制方法包括削波限幅[3]、选择映射(selected mapping,SLM)[4]、主动星座扩展(active constellation extension,ACE)[5]、部分序列传输(partial transmit sequences,PTS)[6]、压扩变换(companding)[7]和载波预留(tone reservation,TR)[8]等。其中预留子载波技术只使用一部分子载波传输数据，其余的子载波被预留出来，专门传输用于抑制峰均比的削峰信号。由于传输数据的子载波和存放削峰信号的子载波相互正交，因此削峰信号不会对数据信号造成干扰。在接收端，削峰信号可以被直接滤除，而不需要发送任何边带信息。

经典的预留子载波峰均比抑制算法中，限幅噪声比(signal to clipping noise ratio-tone reservation,SCR-TR)算法通过使限幅噪声功率比SCR取值最小，设立优化目标，推导PAPR抑制算法的迭代公式；通过工程优化理论，仅选取最大峰值进行处理，有效降低了算法复杂度，并可防止过度削峰带来的带外谱噪声，但算法收敛速度缓慢[9]。

本文针对预留子载波峰均比抑制技术算法收敛速度慢、抑制效率低的问题，研究PAPR抑制问题的凸优化建模和迭代过程的惩罚函数表达式；构建基于预留子载波的联合峰均功率比迭代过程；设计各惩罚函数项的加权组合，分析算法的合理性，并通过仿真验证该算法的PAPR抑制性能、误码率和带外频谱扩散性能。

1　OFDM系统的预留子载波技术

下面给出基于预留子载波技术的OFDM发射系统原理及峰均功率比的定义。

1.1　预留子载波技术原理

基于预留子载波技术的OFDM系统发射系统原理，如图1所示。

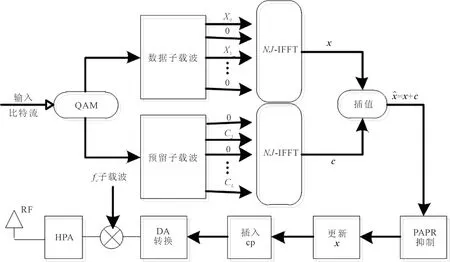
图1　基于预留子载波技术的OFDM发射系统原理

图1中，输入的比特流经过正交振幅调制(quadrature amplitude modulation,QAM)方式调制后，生成频域信号

X=[X0,X1,…,XN-1]T。

数据子载波负责承载频域信号数据X，而预留子载波负责承载频域削峰信号C。J倍过采样后的信号通过NJ快速傅里叶逆变换(inverse fast Fourier transform,IFFT)运算转换为时域信号

x=[x1,x2,…,xn,…,xNJ]T。

同理，得到时域消峰信号

c=[c1,c2,…,cn,…,cNJ]T。

设OFDM系统的子载波总数为N，预留子载波总数为L，过采样率为J。图1中经过NJ点IFFT运算后的时域数据信号可以表示为

其中n=1,2,…,NJ,所以上式可以改写为

其中，j表示虚数单位，xn为n时刻的OFDM时域信号，Xk是QAM调制后的频域信号的第k个元素(k=1,2,…，NJ)，Q为傅立叶变换矩阵，Q矩阵的第m行n列(m,n=1,2,…，NJ)元素为

其中QJ是将矩阵Q中间的N(J-1)个全零列去掉后所得到的NJ行n列子阵。

1.2　峰均功率比的定义

OFDM信号峰均功率比定义为OFDM信号最大峰值功率与平均功率之比，OFDM信号的峰均功率比

其中，E[]表示数学期望。在衡量各类算法抑制OFDM信号峰均功率比的效果时，常采用互补累积分布函数(complementary cumulative distribution function,CCDF)来刻画。CCCDF是OFDM信号的峰均功率比超过指定门限值PPAPR(obj)的概率，定义为

CCCDF(PPAPR(obj))=Pr{PPAPR>PPAPR(obj)}。

2　联合峰均功率比抑制算法

下面给出本文所提出的联合峰均功率比抑制算法的原理和步骤。

2.1　联合峰均功率比抑制算法的原理

经过削波限幅算法[9]处理后的信号可表示为

本文所提出的联合峰均功率比抑制算法是基于凸优化建模构建的[10]，联合算法J可以通过3个变量表示为

其中β为缩放因子，g(·)为阶跃函数，λ为罚因子，NJA为罚函数。

在限幅噪声比(SCR-TR)算法[9]中

在最小平方逼近(least square approximation-tone reservation,LSA-TR)算法[11]中，

xm+1=xm+μcm。

其中μ和cm可分别看作是LSA-TR算法的罚因子和罚函数。cm是第m次迭代后的时域预留子载波信号。罚因子μ是依据最小平方法计算得出的，从而使μcm能够在峰值出现位置尽可能地逼近限幅噪声的幅度。

联合峰均功率比抑制算法的原理，如图2所示。

图2　联合峰均功率比抑制算法原理

2.2　算法步骤

所提出的联合峰均功率比抑制算法的主要步骤总结如下。

步骤1初始化设置。设定峰均功率比抑制目标值PPAPR(obj)，子载波总数N，预留子载波总数L，最大迭代次数Mmax和限幅门限A。时域信号的初始值为x0，峰均功率比初始值为PPAPR(0)。

步骤2将输入信号转换为频域信号X。将预留子载波上的信号初始化为零。经过数据子载波和预留子载波的插值操作后，对X进行NJ点的IFFT运算生成时域信号x。将开关K1置于1，K2置于2，开始迭代运算，此时m=1。

步骤4计算限幅噪声fm=ym-xm。对fm做NJ点的傅里叶变换(fast Fourier transform,FFT)运算，生成Fm。将Fm数据子载波上的信号置为零，从而得到频域削峰信号Cm。Cm经NJ点的IFFT运算转换为时域削峰信号cm，即为LSA-TR方法中的惩罚函数。

步骤5计算LSA-TR方法中的罚因子

步骤6将Fm预留子载波上的信号置为0，并将得到的频域数据信号进行主动星座扩展修正。

步骤7计算cm在xm上的投影值，得到投影系数

其中

步骤8计算SGP-ACE方法中的罚因子

其中元素表示为

步骤9用LSA-TR和SGP-ACE方法中的罚因子分别乘以各自的罚函数，并与SCR-TR方法一起加权组合，构成迭代公式，得到xm+1。其中SCR-TR方法的迭代步长选取LSA-TR方法中的罚因子μm。各算法在加权迭代过程中的权值(缩放因子)可由仿真实验调整。

步骤10计算xm+1的峰均功率比数值PPAPR(m+1)。若PPAPR(m+1)已经达到或超过PPAPR(obj)，停止迭代。如果迭代次数大于Mmax，停止迭代。迭代停止时，将K2置于1，输出xm+1。否则，迭代次数加1，返回第3步，继续进行迭代运算。

3　仿真结果及分析

通过Matlab仿真，比较分析所提出的联合峰均功率比抑制算法的峰均功率比抑制性能、误码率及带外频谱扩散性能。

在以下各种仿真模型中，均设定OFDM系统中的子载波数N=1 024，其中预留子载波数L=54。OFDM符号数为1 000，过采样率J=4。针对过采样后的OFDM时域信号，设定削波门限A=2E{|xm|}。星座调制方式分别采用正交相移键控(quadrature phase shift keyin,QPSK)或正交幅度调制(quadrature amplitude modulation,16QAM)。无线信道模型分别选取高斯信道(additive white Gaussian noise,AWGN)模型或莱斯(Rician)信道模型。

3.1　联合峰均功率比抑制算法的抑制效果

所提出的联合峰均功率比抑制算法和其他6种基于预留子载波技术的经典峰均功率比抑制算法的PAPR抑制性能进行了对比。

这几种经典算法分别是：凸集投影(projections onto convex scts-tone reservation，POCS-TR)算法[13]、削波限幅(clipping-TR)算法[9]、限幅噪声比(SCR-TR)算法[9]、主动星座扩展(active-set)算法[14]、最小平方逼近(LSA-TR)算法[11]和智能梯度投影主动星座扩展(SGP-ACE TR)算法[5]。峰均功率比抑制性能比较，如图3所示。

图3　峰均功率比抑制性能比较

如图3所示，仿真中同时给出了原始OFDM信号的峰均功率比互补累积分布函数(CCDF)曲线，从而可以清晰地观察不同算法的峰均功率比抑制效果。

如图3所示，仅经过1次迭代运算(m=1)，所提出的联合峰均功率比抑制算法的峰均功率比的抑制性能已经优于POCS-TR、Clipping-TR、SCR-TR和active-set这4种算法各自经过6次迭代运算(m=6)所达到的抑制效果。所提出的联合峰均功率比抑制算法经过2次迭代运算(m=2)后的峰均功率比抑制性能优于LSA-TR和SGP-ACE TR算法分别经过6次迭代运算所能达到的抑制效果。经过3次迭代运算(m=3)后，所提出的联合峰均功率比抑制算法在CCCDF=10-3时，峰均功率比抑制能力可以达到6.359 dB。在相同峰均功率比抑制性能的要求下，所提出的联合峰均功率比抑制算法需要的迭代次数明显小于其他6种经典子载波预留算法。

3.2　联合峰均功率比抑制算法的误码率比较

所提出的联合峰均功率比抑制算法与3中经典算法的误比特率(bit error ratio,BER)在高斯信道(additive white Guassian noise，AWGN)和QPSK星座调制方式下比较，如图4所示。

图4　高斯信道下的误比特率比较

如图4所示，所提出的联合峰均功率比抑制算法在分别经过1、2、3次迭代后的BER曲线几乎重合在一起。迭代次数的增加并不会明显恶化BER性能。当比特信噪比小于7 dB时，所提出的联合峰均功率比抑制算法的BER性能与SGP-ACE TR和LSA-TR算法经过6次迭代后的BER曲线几乎重合。当比特信噪比大于7 dB小于10 dB时，所提出的联合峰均功率比抑制算法的BER性能开始下降，但仍然优于SCR-TR算法的BER性能。

不同峰均功率比抑制算法在16QAM星座调制方式下对比，如图5所示。

图5　高斯信道的误比特率比较(16QAM)

通过高斯信道(AWGN)后的误码率曲线。所提出的联合峰均功率比抑制算法的误比特率(BER)随迭代次数的增加，没有明显的恶化。第3次迭代后的BER性能甚至略优于第2次迭代的BER性能。与其他3种经典算法相比，当比特信噪比小于9 dB时，联合峰均功率比抑制算法仍优于SCR-TR算法的BER性能。对比图3可知，联合峰均功率比抑制算法能够用BER性能的略微下降换取峰均功率比抑制效果的显著提高。

不同峰均功率比抑制算法在QPSK星座调制方式下，通过莱斯信道(Rician)后BER特性如图6所示。

图6　莱斯信道下的误比特率比较

当信噪比小于11 dB时，所提出的联合峰均功率比抑制算法在迭代1、2、3次后的BER性能优于SGP-ACE TR和SCR-TR算法各自迭代6次后的BER性能。迭代次数的增加并不会造成联合峰均功率比抑制算法的BER性能明显恶化。

3.3　联合峰均功率比抑制算法的功率谱密度比较

分别经过所提出的联合峰均功率比抑制算法和其他3种经典PAPR抑制算法优化后，OFDM信号的功率谱密度(power spectral density,PSD)曲线，如图7所示。

图7　不同算法在QPSK调制下的功率谱密度比较

PSD曲线的“帽檐”越高，说明该算法的频谱扩散越严重。为了便于比较，同时给出了原始OFDM信号的PSD曲线。由图7可见，SGP-ACE TR算法的带外频谱扩散性能最差。所提出的联合峰均功率比抑制算法经过1、2、3次迭代处理后的PSD性能接近SCR-TR和LSA-TR算法，且明显优于SGP-ACE TR算法。

4　结语

本文提出基于预留子载波的联合峰均功率比抑制算法，研究该算法的峰均功率比抑制性能与误码率、带外频谱扩散性能的相互折衷。本文的主要贡献在于：

(1)参照峰均功率比抑制问题的凸优化建模和惩罚函数表达式，对多种经典子载波预留算法进行理论分析，找出每种算法能够使迭代过程快速收敛的惩罚函数。

(2)对SCR-TR、SGP-ACE TR和LSA-TR的峰均比抑制惩罚函数进行加权组合，生成联合峰均功率比抑制算法的迭代过程。

(3)通过仿真实验分析联合峰均功率比抑制算法的峰均功率比抑制效果。评估该算法高性能的峰均功率比抑制效果与误码率和带外频谱扩散性能之间的折衷。

(4)对比联合峰均功率比抑制算法与其他经典峰均功率比抑制算法的各项性能。

通过实验分析，联合峰均功率比抑制算法仅需2次迭代，便可以超越其他经典算法经过6次迭代才能达到的峰均功率比抑制效果。由迭代次数大幅下降所节省的优化时间较为可观。联合峰均功率比抑制算法的BER性能在比特信噪比相对较小的信道环境中更具优势。该算法的带外频谱扩散性能没有明显的恶化。