一种改进的大规模MIMO线性预编码算法

张继荣,吕沙沙

(西安邮电大学 通信与信息工程学院， 陕西 西安 710121)

在大规模多输入多输出(multiple input multiple output,MIMO)[1]系统中，基站端采用大规模天线阵列来提升系统性能，随着基站天线数目的增加，接收端译码的复杂度会越来越高，为此可以在基站端应用预编码技术来消除用户之间的干扰，进而可以降低终端信息处理复杂度。

目前广泛应用的预编码算法分为两类，一类是非线性预编码算法，主要包括脏纸(dirty paper coding,DPC)预编码[2]和汤姆林森-哈拉希玛预编码(Tomlinson Harashima precoding,THP)[3]。另一类是线性预编码算法，主要包括最小均方误差(minimum mean squared error,MMSE)预编码算法[4]、迫零(zero forcing,ZF)[4]预编码算法、块对角化[5](block diagonalization,BD)预编码算法。研究表明，在大规模MIMO场景下，也就是天线数目达到一定数量时，线性预编码技术可以达到与非线性预编码技术相同的性能[6]。基于Neumann级数展开的预编码算法具有较低的复杂度，但是其误码率性能并没有提升[7]。文[8]提出了一种混合预编码算法，但是在多用户场景下，系统的误码率和复杂度较高。优化的块对角化(optimized block diagonalization,OBD)预编码算法[9]在求解预编码矩阵时没有考虑系统噪声，且在求解时采用了复杂度较高的奇异值分解(singularly valuable decomposition,SVD)，不适合在大规模MIMO系统中使用。

为了降低算法的误码率和复杂度，本文拟提出一种改进的BD预编码算法。该算法首先利用正规迫零(regular zero forcing,RZF)预编码算法的预编码矩阵作为信道矩阵的伪逆，并采用正三角(orthogonal triangular,QR)分解求得该矩阵的标准正交基，将下行的多用户MIMO系统被分解为平行的单用户信道，并求得每个用户的等效矩阵，最终求得系统各用户的预编码矩阵。

1　大规模MIMO系统模型

在单小区多个用户场景下，大规模MIMO系统模型[1]，如图1所示。

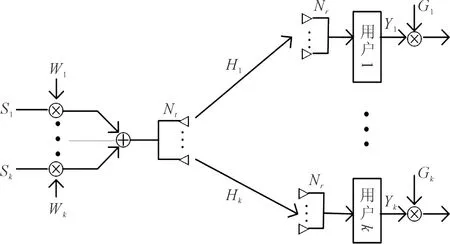
图1　大规模MIMO系统模型

图1中，系统同时服务K个用户；系统为第k(k=1,2,…，K)个用户发送的数据[9]

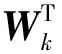
用户配备的接收天线数为Nr，且K×Nr≤Nt；信道检测矩阵[9]

Gk=diag{G1,G2,…,GK} 。

第k个(k=1,2,…,K)用户的接收信号

(1)

其中，归一化因子

用来保证基站发送的总功率为Pt，且

E[‖sk‖2]≤Pt。

nk是系统噪声矩阵，满足均值为0方差为1的高斯随机变量。式(1)第一项为用户k的有用信号，第二项为其他用户对目标用户的干扰，第三项为系统噪声。可以在系统的发送端采取预编码算法来降低式(1)中的干扰项对期望信号的影响，并将以此为出发点来求出预编码矩阵Wk。

2　改进的预编码算法

BD预编码算法是系统有多个用户时最常用的预编码算法，该算法通过在基站端对发送信号进行BD预编码处理，使用户间的干扰可以完全被消除。通过将ZF预编码和BD算法相结合，将ZF算法的预编码矩阵作为信道矩阵的伪逆，并对它的级联矩阵进行SVD分解从而可以计算出各个用户的预编码矩阵[9]，然而使用这种算法求解预编码矩阵时并没有考虑系统噪声，且计算时需要进行两次SVD分解，计算复杂度大。

2.1　求解平行单用户系统的等效信道

ZF预编码算法虽然可以消除用户间的干扰，但并没有考虑噪声的影响，而RZF[10]预编码算法正好可以弥补这个缺陷,且当天线数目Nt和用户数K很大时，RZF预编码算法成为大规模MIMO系统中最优的预编码算法之一[10]。因此本文将RZF算法与BD算法相结合，RZF预编码矩阵

(2)

其中，H为信道矩阵；δ是正则化系数[11]，它的值为用户K除以基站的发射功率Pt，Pt=‖s‖2，s为系统的发射信号向量。由式(2)可知，RZF预编码矩阵是个伪逆矩阵，因此首先定义第k个用户的等效信道矩阵

为了不改变总的发射功率，对矩阵Pk进行QR分解[12]

2.2　求解各用户的预编码矩阵

Σ=diag {Σ1,Σ2,…,Σk}

的对角线元素进行注水得到。此时得到的用户k的预编码矩阵

3　实验结果及分析

3.1　实验条件

利用Matlab软件进行仿真，仿真用户数从1到61，天线数目从8到128，信道为平坦的衰落信道，且服从瑞利分布，噪声信号为高斯白噪声，系统采用QPSK进行调制。

3.2　算法误码率分析

基站天线数从8到128，系统同时服务4个用户，每个用户有2根接收天线时，改进的预编码算法、传统BD预编码算法以及文[9]提出的OBD预编码算法的误码率性能随着基站天线数目增加的变化情况，如图2所示。

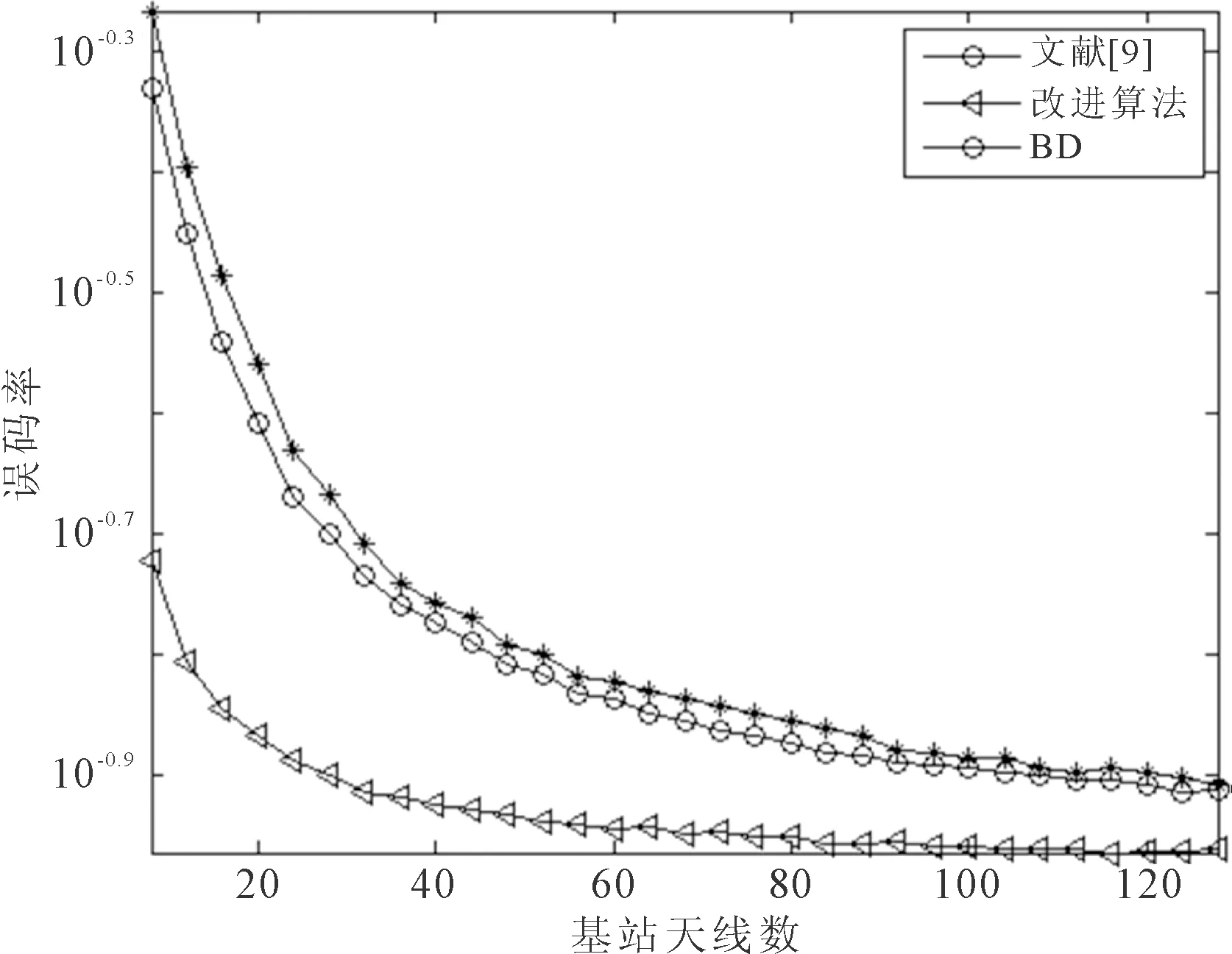
图2　误码率性能随基站天线数目的变化情况

从图2可以看出，随着基站天线数目的增多，系统的误码率是逐步降低的，这就是多天线带来的优势。改进的预编码算法误码率性能最优、传统BD预编码算法最差。这是因为改进预编码算法不仅可以消除用户间干扰，且考虑到系统噪声，因此误码率性能最优。在天线数目为128时，改进预编码算法误码率为0.109 5,文献[9]的OBD算法的误码率为0.123 8，误码率降低了11.5%。

基站配备128根天线，用户数目从1到61个时，每个用户有2根接收天线，信噪比为5 dB时，3种预编码算法的误码率随用户数的变化情况，如图3所示。

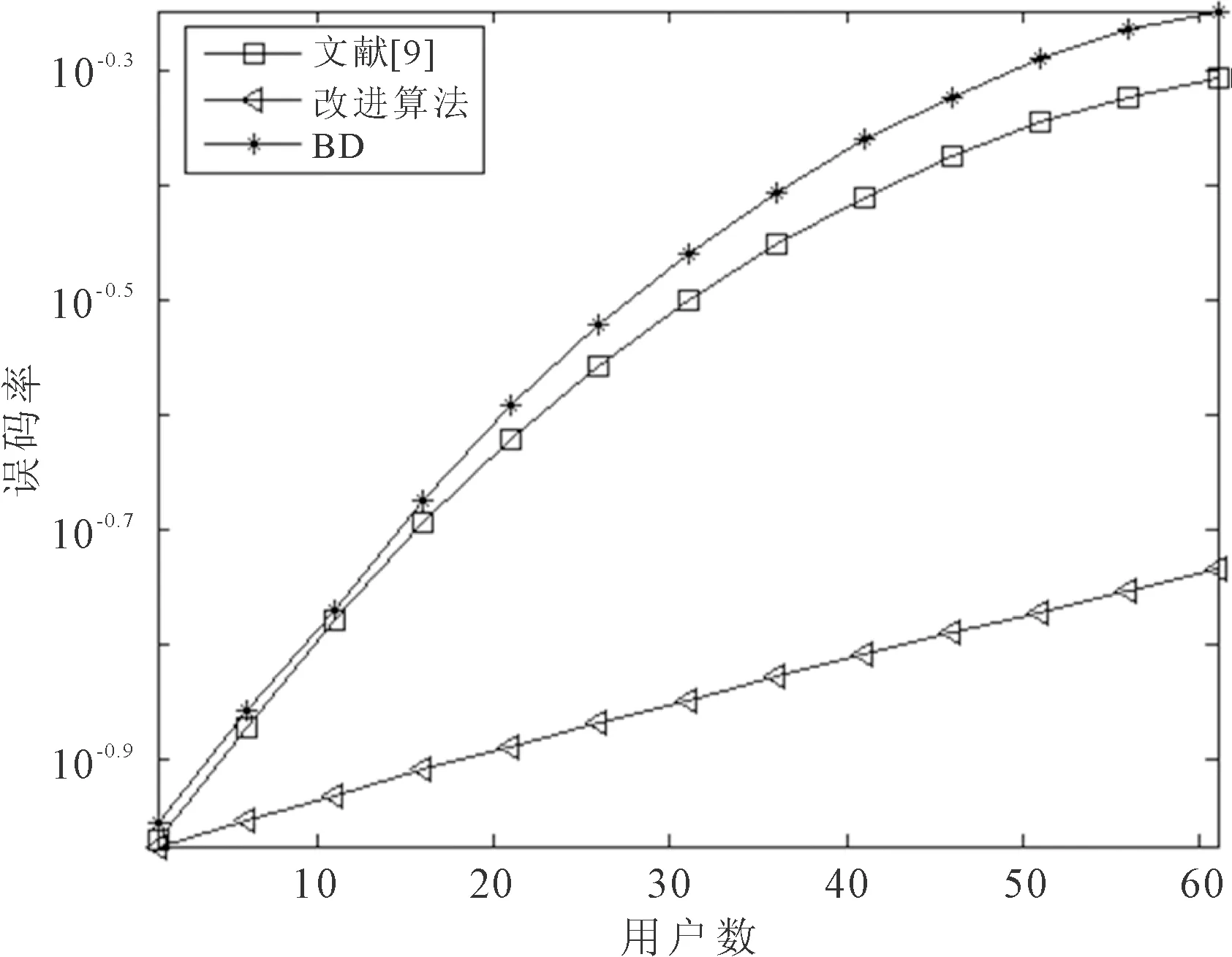
图3　误码率性能随用户数的变化情况

从图3可以看出，随着用户数的增多，3种预编码算法的误码率都是逐步增大的，改进算法的误码率性能最优，传统BD算法误码率性能最差。当用户数为61时，改进算法误码率为0.184 7,文[9]提出的OBD算法的误码率为0.493 2。误码率下降了62%，这说明改进算法是可以应用于大规模MIMO系统中的，可以同时服务于多个用户，并且用户数越多，改进算法优势越大。

3.3　算法复杂度分析

利用浮点运算flop数目[13-14]进行复杂度分析，一个flop表示一次实数乘法或加法运算，一次复数乘法需要6个flop，一次复数加法需要2个flop。为了进一步揭示预编码算法的运算复杂度与系统天线配置的关系，本节对文[9]提出的OBD算法以及本文的改进算法的复杂度进行分析，两种算法的复杂度与基站配备的发送总天线数Nt、接收天线总数Nr、每个用户的接收天线数Ne以及用户个数K的关系，如表1和表2所示。

表1　文[9]预编码算法的运算复杂度

表2　改进预编码算法的运算复杂度

基站配备128根发送天线，同时服务的用户数从1到61，每个用户的接收天线数为2时，两种算法的复杂度随用户数的变化情况，如图4所示。

从图4可以看出，改进预编码算法复杂度较文[9]的OBD算法要低，这是因为文[9]提出的预编码算法是将ZF算法的预编码矩阵作为信道矩阵的伪逆，并对其级联矩阵

图4　算法复杂度随用户数的变化情况

5　结语

针对大规模MIMO系统，基站配置多达百根天线，系统同时服务多个用户的情况，本文提出了一种基于BD预编码算法的改进算法。该算法首先对RZF算法的预编码矩阵进行QR分解，将系统分解为平行单用户系统，然后对每个用户的等效信道矩阵进行SVD分解，最终求得各用户的预编码矩阵。当基站天线数为128、同时服务61个用户时，改进算法、文[9]算法的误码率分别为0.109 5、0.123 8，误码率降低了11.5%，浮点数分别为1.379×108、1.045×1010,复杂度降低了1.031×1010。这说明改进算法不仅降低了系统的误码率而且改善了运算复杂度。