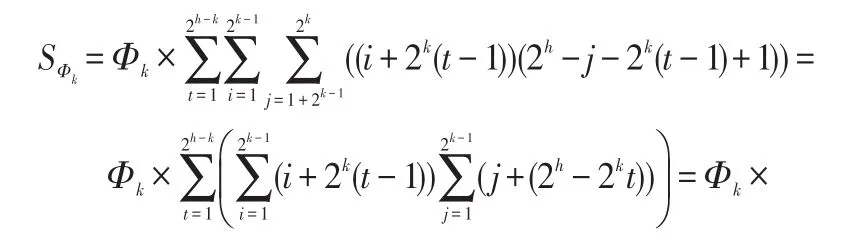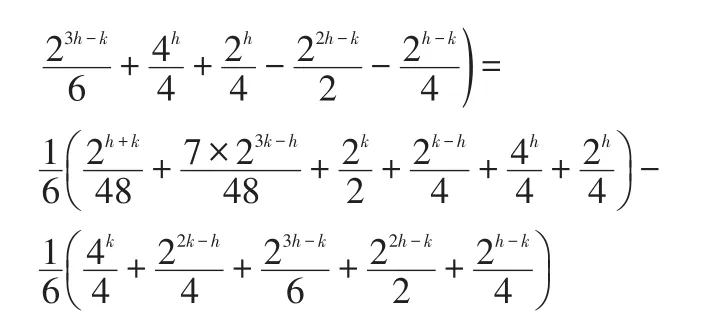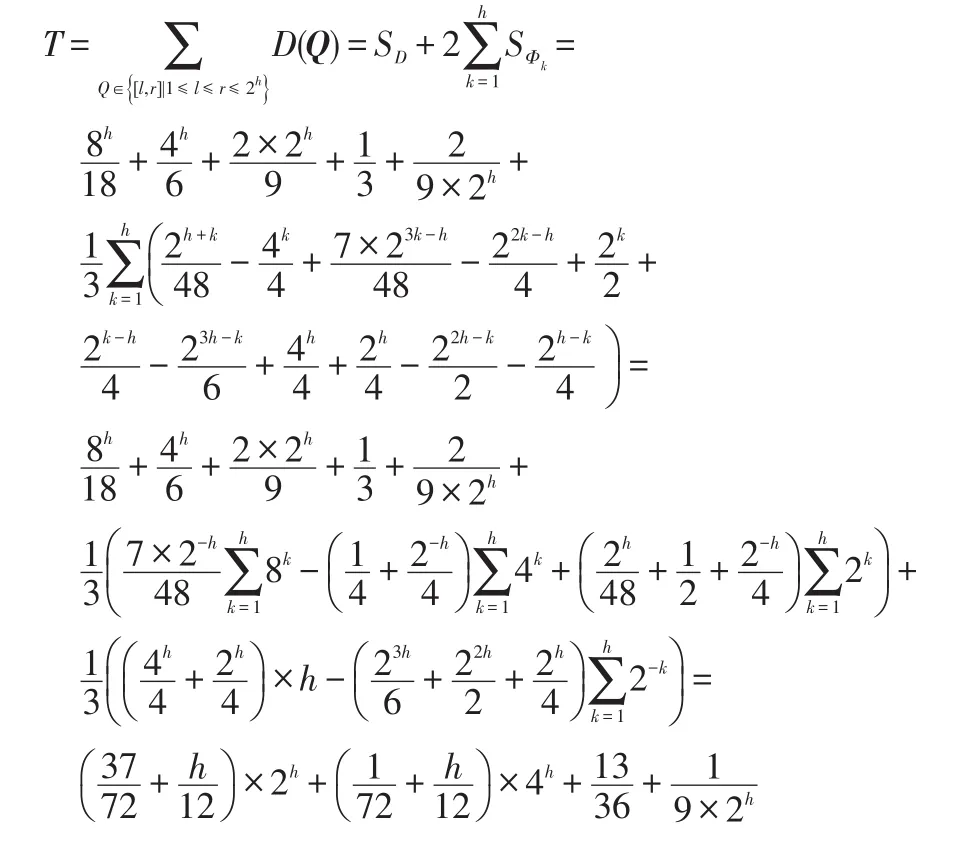矩阵机制下差分隐私数据发布方法的误差分析*
吴英杰,陈靖麟,蔡剑平,王一蕾
福州大学 数学与计算机科学学院,福州 350108
1 引言
在现实生活中,由于数据统计和科学研究的需要,许多研究机构或组织都会对外发布数据。如何保证所发布的数据既是可用的,又不会泄漏数据中所包含的个体的隐私信息,已成为当前数据挖掘与信息共享领域一个十分热门的研究课题。针对此类问题,国际上众多研究人员对隐私保护数据发布进行了深入研究,提出了不少隐私保护数据发布模型。然而,现有的隐私保护模型大多以匿名为基础,这些模型均需要特殊的攻击假设和一定的背景知识,因此具有很大的局限性。为此,Dwork等人[1-3]提出了差分隐私模型,该模型适用于各种背景条件,并且具有严格的数学证明,得到了广泛的认可。基于该隐私保护模型,学者们开展了很多相关研究工作,内容涉及直方图发布[4-8]、连续数据发布[9]、空间划分发布[10-11]、智能数据分析[12-14]等。
差分隐私算法通过对数据添加随机噪声来实现隐私保护,因此在保护隐私的同时必然会产生相应的数据误差。算法的误差是评价算法的重要指标,因此对于差分隐私算法来说,计算均方误差是该算法最为基本也是最为重要的工作。然而,现有的大部分差分隐私算法对均方误差的估计,往往是基于实验或者采用先统计各变量的均方误差再累加的方法。该做法使得难以对算法的均方误差进行定量分析,或者使得分析过程极为复杂,不能有效、简洁地让读者了解该算法的精确性,给读者在算法的理解上造成一定的困扰。
近年来,许多研究学者提出了多种差分隐私数据发布算法,其中多数集中在两方面:一是以k-叉树的形式对数据进行处理,然后采用一致性约束的分层结构差分隐私算法;二是利用策略矩阵进行变换,加噪后通过还原矩阵进行还原的基于矩阵机制的差分隐私算法。其中,Qardaji等人[15]对以Boost为代表的分层结构差分隐私算法的均方误差进行了有效的理论分析,并提出相应的求解方法。而以Prievlet算法为代表的基于矩阵机制的差分隐私算法尚缺乏相应的理论分析,本文通过研究现有的差分隐私数据发布算法对均方误差的计算,并结合矩阵运算的相关理论,提出基于矩阵运算的均方误差计算方法。本文方法能够将基于矩阵机制的差分隐私算法的均方误差进行一般化处理,是一种具有普遍性的方法,能够简洁有效地求出基于矩阵机制的差分隐私算法的均方误差。本文以Prievlet算法[4]为例进行详细的分析、推导,其他算法可通过类似推导完成。
本文的主要贡献如下:
(1)基于矩阵运算以及协方差的计算,从理论上分析任意固定查询区间下Prievlet差分隐私算法的均方误差,得出求解公式。
(2)在第一步的基础上,求解Prievlet算法随机查询区间下的均方误差,推导出平均均方误差的公式,得出Prievlet算法误差的渐进阶。
(3)提出精确度指标,对其进行推导、说明,并对一些算法进行求解,该指标能够简洁有效地说明差分隐私算法的精确性。
(4)通过实验验证文中所求得的均方误差公式的正确性。
2 基础知识与问题提出
2.1 基础知识
差分隐私保护模型是一种强健的隐私保护框架,由Dwork等人[1]首次提出。差分隐私保护模型在数据发布过程中,不论攻击者具备何种背景知识,都能保证隐私数据不泄露。
定义1(ε-差分隐私[1])设有一对兄弟数据集D1和D2(当且仅当D1和D2中的记录只有一条不同),若一个发布算法A在兄弟数据集D1和D2上的所有可能的输出满足以下条件,则称算法A满足ε-差分隐私。
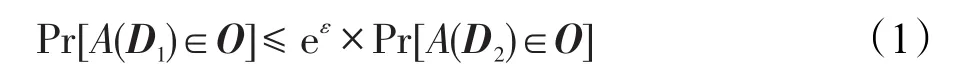
定义2(ε-敏感度)统计某数据库中的数据集D1和D2分别得到两组由列向量表示的结果:Q(D1)=(x1,x2,…,xn)T,Q(D2)=(x1′,x2′,…,xn′)T。那么查询集合Q的敏感度ΔQ满足以下定义:

在差分隐私中,更为经常使用的范数为1-范数,即p=1。文中的敏感度如无特殊说明均以1-范数为度量。敏感度表明了当D仅改变一条记录的情况下对统计结果Q(D)的影响情况。一般而言敏感度越大,Q(D)受影响的程度越强,需要添加的噪声也越强。
2.2 问题提出
差分隐私数据发布算法经常需要将原数据进行线性变换后再进行发布,此时计算出每个变量的均方误差再进行累和并不能反映该算法的均方误差。考虑如下情景:某差分隐私算法A运行后输出两个随机变量x1、x2,并计算它们的均方误差D(x1)、D(x2)用于评价算法A。假如算法B在算法A的基础上实现,其需要输出z,满足z=x1+x2。根据概率统计的原理可知,新算法输出变量z的均方误差为:
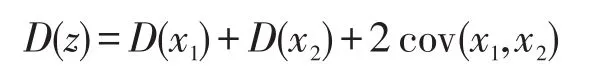
而由于协方差的存在,仅凭D(x1)、D(x2)是无法计算出D(z)的。该例子说明完整的均方误差分析应该包含随机变量之间的协方差。而在概率统计领域,人们常常使用协方差矩阵来表示一组随机变量间的协方差(主对角线上的值表示均方误差)。设X=(x1,x2,…,xn)T为一个随机变量,则它的协方差矩阵为:
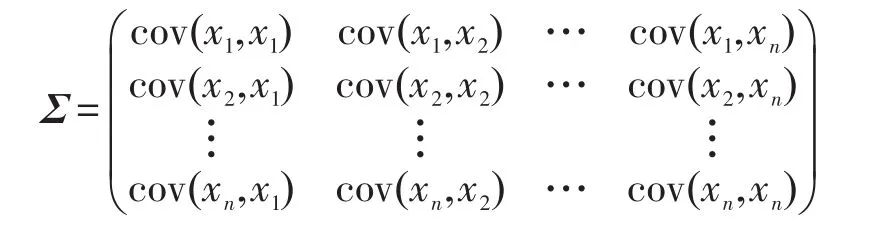
以随机向量L͂n为例,它的每一个分量均是一个满足Lap(1)(Laplace简称Lap)分布的独立随机量,显然随机量间的协方差为0。而Lap(1)分布的均方误差为2,则 L͂n的协方差矩阵为:

然而,仅仅使用协方差矩阵进行误差分析远远无法满足大多数应用的需要。绝大多数算法涉及了随机向量间的线性变换。为此,本文在误差分析时将使用以下定理。
定理1[16]若随机向量Z与X之间存在线性关系Z=AX(A为矩阵),且已知X的协方差矩阵表示为RX,则Z的协方差矩阵为RZ=ARXAT。
由协方差矩阵的性质可知,其对角线元素为各随机变量的均方误差,因此人们通常利用函数trace(*)求解最终的均方误差。由于忽略了协方差,该方法得出的均方误差不能精确地表示算法的误差。
3 Prievlet算法的误差分析
3.1 Prievlet差分隐私算法
Prievlet差分隐私算法[4]通过对数据进行前置处理来提高数据发布的精度。这种方法受到哈尔小波变换的启发,使用哈尔小波变换矩阵先对原始数据进行压缩,再对压缩后的数据添加拉普拉斯噪声使其满足差分隐私。然后,将原始数据与压缩数据组合在一起构建一棵形如图1具有8个节点的Prievlet二叉树,其中叶子节点为原始数据,自下而上,对于每个非叶子节点,其权值为左子树叶子节点的权值之和减去右子树叶子节点的权值之和。构造过程见算法1。

Fig.1 Prievlet-two-fork-tree with 8 nodes图1 8个节点Prievlet二叉树
算法1Prievlet差分隐私算法
输入:原始数据向量vi(1≤i≤2h),隐私预算ε。
1.输入初始数据。
2.对数据进行压缩转换。每个非叶子节点的值等于左子树叶子节点的权值之和减去右子树叶子节点的权值之和,具体公式如下所示:

3.敏感度Δ=h+1,对所有ck添加拉普拉斯噪声得到满足差分隐私的压缩系数
由算法1所得到的压缩系数,可通过式(4)还原,求出所有满足差分隐私算法的输出数据:
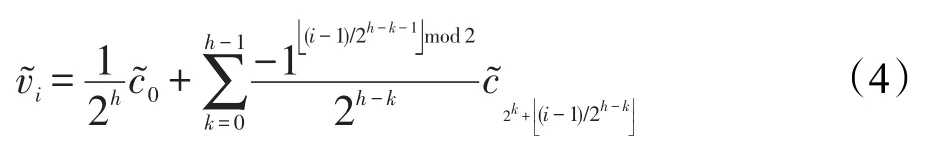
Prievlet算法适用于区间查询,其查询均方误差复杂度为O(lb3n),n=2h。相比于其他二叉树方法,使用小波变换方法压缩的数据,不存在不一致性问题,无需采用任何后置处理方法来提高算法的精确性。
3.2 分析Prievlet算法的均方误差
通过研究Prievlet算法可以发现,数据经过Prievlet算法的变换是线性的,这意味着可以用一种基于矩阵的运算来表示Prievlet算法的变换过程。因此,可以根据Prievlet算法的变化过程构造相对应的策略矩阵,从而对Prievlet算法的均方误差进行有效的分析。
首先,需将Prievlet算法的变换过程用矩阵进行表示。根据算法1,由ck的计算式(3),可以得到Prievlet算法的策略矩阵,同时根据式(4)可以得到Prievlet算法的还原矩阵。例如,当数据量的大小为4时,根据以上方法,可以得到对应的策略矩阵和还原矩阵。
Prievlet算法的策略矩阵:
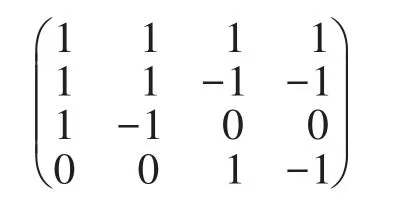
Prievlet算法的还原矩阵:

其中数据通过策略矩阵变换可得到压缩系数,然后加噪后的压缩数据通过还原矩阵可得到加噪后的数据。
根据文献[4]可知,Prievlet算法是在经过策略矩阵变换后的系数上添加噪声,因此对策略矩阵不需要进行分析,而对于Prievlet算法的还原矩阵B,直接对加噪后的系数进行线性组合来完成还原,是均方误差的主要来源,接下来将对其进行详细的分析。矩阵B的构建可根据式(4)得出,图2是还原矩阵中单行(单个数据)的求解流程图,整个还原矩阵B的求解见算法2。

Fig.2 Flow chart to solve the p line in restore matrixB图2 还原矩阵B第p行求解流程图
算法2求解Prievlet的还原矩阵


通过算法2得到还原矩阵后,结合定理1,可以得到通过Prievlet算法变换后的数据的协方差矩阵:
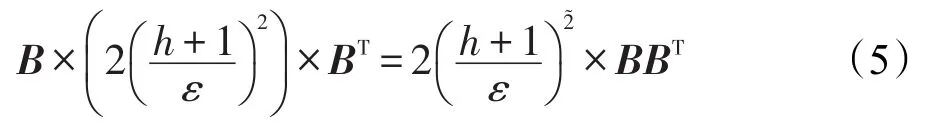

由矩阵的乘法可知Σij为矩阵B的第i行和第 j行进行点乘的结果,且满足如下定理。
定理2由矩阵B的第i行和第 j行点乘所得到的Σij满足如下公式:
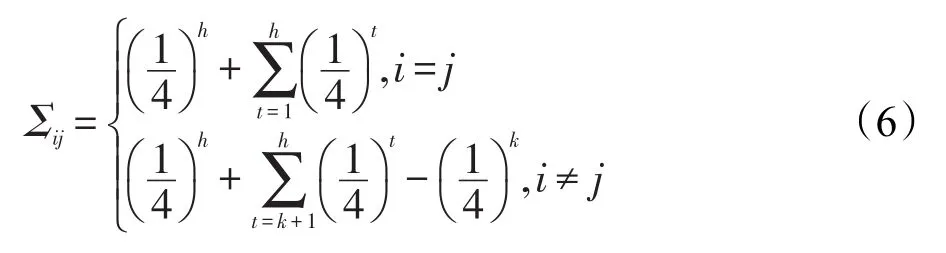
式中,k为节点i与节点j的最近公共祖先的高度(见图1)。可由该公式计算求得:其中⊕表示二进制表示下的按位异或运算。
证明当i=j时,由算法2可得,恒成立。然后t从h到1循环,每次循环都将一个由0置为因此,除Bi,1以外,B的第i行存在且仅存在一个元素从而:


则Σij计算如下:
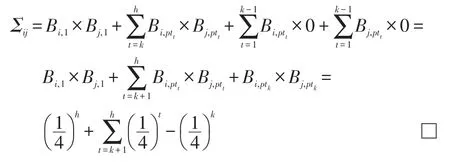
为了便于计算,本文对式(6)进一步化简,得到与之等价的式(7):
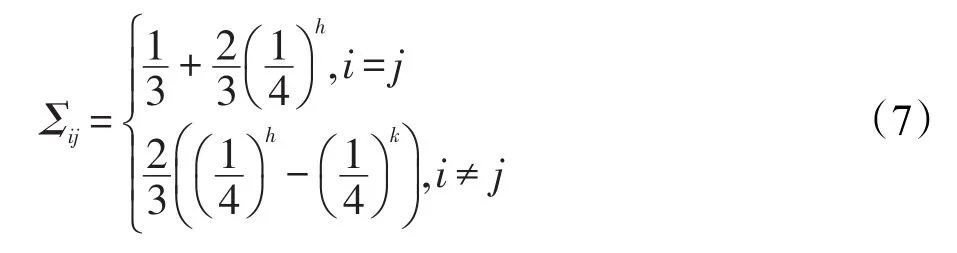
又令Φk表示两节点最小公共祖先层数为k时的协方差,则Φk满足如下递推关系:

分析完Prievlet算法的均方误差,下面对Prievlet算法的均方误差进行求解。
3.3 求解Prievlet算法的均方误差
求解Prievlet算法的均方误差将分两步进行:首先对任意固定查询区间的均方误差进行求解;然后求解随机查询区间的均方误差。
3.3.1 求解任意固定查询区间的均方误差
将经过Prievelet算法变换后的数据用向量的形式表示成则可以将查询区间[l,r]表示成向量,那么查询结果为
根据定理1和式(5),得到这个查询的均方误差为:
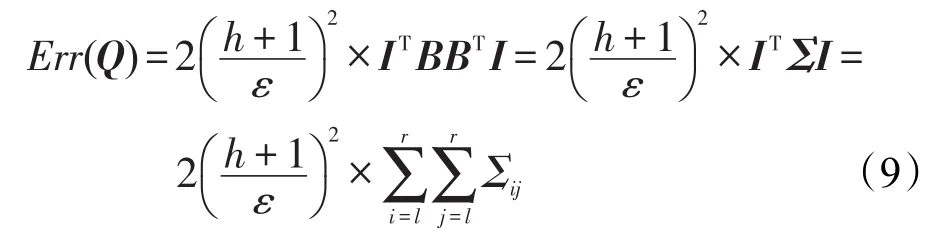
式(9)需要进行矩阵乘法运算,该运算的复杂度较高。而从2.1节的分析结果可以发现协方差矩阵存在规律,可以由定理2以及式(6)计算得出协方差矩阵中的任意一个值。利用上述特点,本文提出一个可以快速计算Prievlet算法区间查询的均方误差的算法。
由定理2可以得出,对于节点i与节点 j,它们的均方误差为这意味着每对节点的均方误差只与最近祖先高度有关。那么对每个非叶子节点进行考虑,只需计算出以该节点为最近公共祖先叶子节点的对数,再乘上对应的协方差即可。
以图3为例,共有8个叶子节点,查询区间为[3,7]。图中条纹标注节点是查询区间覆盖了该节点的部分区间,而用灰色表示的点是整个区间都被查询区间覆盖。例如:节点c3所表示的是[4,8]这个区间,查询区间[3,7]只覆盖了其中一部分;而节点c5则完全被查询区间[3,7]覆盖。
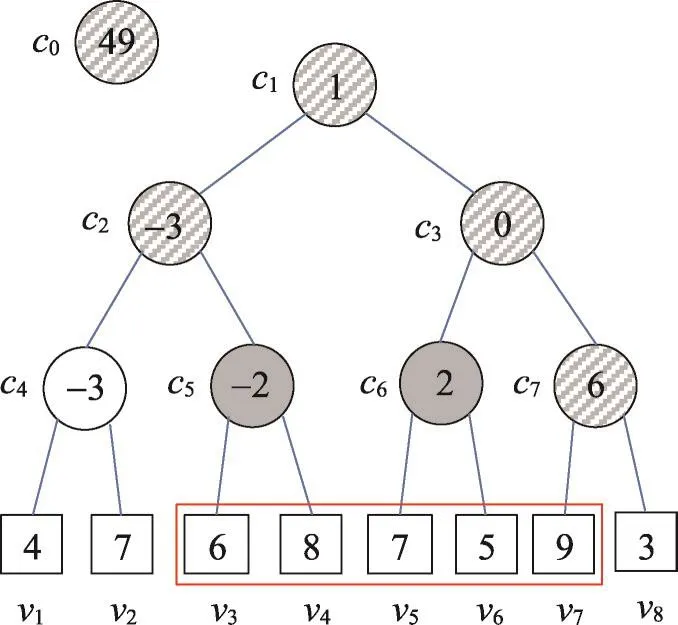
Fig.3 Example of[3,7]query of Prievlet algorithm图3 Prievlet算法查询[3,7]的示例图
对于灰色的节点,是被查询区间完全覆盖的,那么以该节点为最近公共祖先的节点对数可以由左右子树叶子节点个数的乘积得到。根据这个二叉树的性质可以知道,如果该节点在第k层,那么其覆盖范围是2k,左右子树叶子节点个数都为2k-1。因此,如果一个节点是第k层节点,那么以该节点为最近公共祖先的叶子节点对数为4k-1。然后只需再计算出第k层灰色节点的个数即可,可由以下公式计算:

图3中的条纹节点是查询边界上的节点,显而易见,这种节点在每一层最多会出现2个,因此可以直接枚举进行求解。假设节点cx是第k层的节点,覆盖区间为[lx,rx],可以得出以节点cx为最近公共祖先的叶子节点对数为|P|×|R|,其中
除了考虑协方差之外,还需要对各个变量各自的均方误差进行考虑,即Σ矩阵中的对角线元素Σii。由定理2可以发现,这些均方误差都是固定的,只需将该均方误差乘上区间的长度r-l+1即可得出。
根据上述分析,本文提出了一种求解Prievlet差分隐私算法任意区间查询的均方误差(算法3)。在Prievlet算法中,敏感度和隐私预算ε都是一个固定的值,这两个参数只会影响所需添加的噪声大小,而对于采取相同噪声机制的差分隐私算法而言,不会产生影响,为了方便计算分析,暂时不予考虑,只考虑均方误差的系数。
算法3求解任意固定区间查询的均方误差系数


由算法3得出的Rerr,可以得出查询区间[l,r]的均方误差,如下所示:

分析算法3可以发现,其时间复杂度为O(h),即O(lbN),只需遍历一次1到h就能得出答案。因此该算法能够完成海量数据量下的均方误差的求解任务。
3.3.2 求解随机查询区间的均方误差
算法3可以快速有效地求得任意固定查询区间下Prievlet算法的均方误差,但固定区间查询的均方误差不能体现该算法平均情况下的均方误差,因此下文将在算法3的基础上对随机查询区间下Prievlet算法的均方误差进行求解,得出该算法平均情况下的均方误差。
观察式(9),对于所有查询来说,Prievlet算法添加的噪声是一样的,其不同之处是ITΣI的值不同,本文称这部分为均方误差系数。接下来将对均方误差系数进行重点分析。
观察均方误差系数ITΣI可以发现,该计算过程等价于取出Σ矩阵中的一个子矩阵,从第l行到r行,l列到r列,然后将子矩阵中所有元素相加的结果。
以下是一个在8个节点下,查询区间为[3,7]的例子,其中矩阵是该查询规模下的协方差矩阵,虚线框内是被取出来的子矩阵。

接下来,对Prievlet算法的平均均方误差进行求解。在平均情况下,可以认为对于所有的查询区间[l,r],l≤n,l≤r≤n出现的概率都是均等的。可将上文中ITΣI的求解方式进行变换,考虑对于每个Σij会被多少个查询区间所用到。计算公式如下所示:

若只考虑i≤j的情况,式(12)可以进一步化简为 cntΣij=i×(2h-j+1)。
i>j时,可以利用Σ矩阵的对称性进行求解,即cntΣij=cntΣji。
从上文的分析可以看出,协方差矩阵Σ中有很多相等的值,因此可按不同的值进行分类讨论,以提高求解效率。从定理2中可以看出求解总体的均方误差可以分为两步。
首先求解两个不同节点的均方误差系数之和。根据两节点的最近公共祖先的高度划分,假设高度为k,那么Σij满足Σij=Φk。然后用式(13)计算这些值被每个区间计算到的总和SΦk。如下所示:

式(13)的计算过程见附录。
然后求解每个查询区间的各个元素的独立均方误差总和SD。计算过程如下:
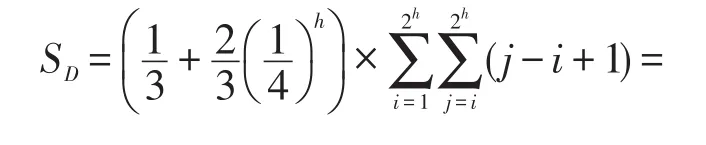

最后,将上述两个步骤的计算结果结合,得到区间查询的均方误差系数总和:
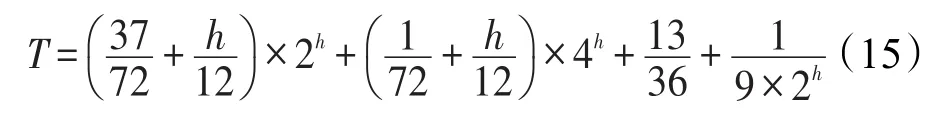
式(15)计算过程见附录。
根据上文方法求出查询区间的均方误差系数总和之后,只需将其除以区间的总个数即可得到Prievlet算法在进行区间查询时均方误差系数的平均情况。计算过程如下:

h→∞时式(16)的极限为:


实验表明,当 h>10时,式(16)与式(17)计算结果的差别可以忽略不计。
最后只需要将根据式(16)得到的均方误差系数乘上Prievlet算法的均方误差,就可以得到平均情况下的均方误差:

上述两部分,基本的噪声误差不可变,取决于用户想要保护隐私的程度。而误差系数主要由所采用的算法和数据规模确定,其中数据规模取决于应用的需要,不随所采用算法的改变而改变。为反映差分隐私算法的性能,下文将对误差系数进行处理,将与算法性能本身无关的部分去掉,提出一种直观的、能够反映算法性能的评价指标。
4 O(lb3N)精确度指标
在现有的差分隐私数据发布领域,目前所有算法的均方误差渐进阶最低能达到O(lb3N)[15]。因此,本文将针对此类算法提出差分隐私O(lb3N)精确度指标,具体定义如下:
定义3(O(lb3N)精确度指标)已知差分隐私算法Α与该算法所处理的数据规模为N。令表示在该数据规模下算法Α产生的平均均方误差系数函数,则该算法O(lb3N)精确度指标k表示为:

以Prievlet算法为例,O(lb3N)精确度指标k计算如下:

因此,随机区间查询下的Prievlet算法的O(lb3N)精确度指标为6。
与传统的描述均方误差复杂度的方法相比,上文提出的精确度指标能更加形象地表示差分隐私算法的性能。一般而言,精确度指标相同的算法,精确度方面性能相近;而对于精确度指标不同的算法,随着数据规模的增大,精确度指标越低的算法,误差越大。因此,该指标能够准确地反映差分隐私算法的精确性。
另一方面,研究表明,绝大多数算法的O(lb3N)精确度指标均为正数,这使得结果更加直观,能够简洁地反映差分隐私算法的精确性,便于人们对算法性能的研究和比较分析。经过理论分析,常见的3种差分隐私算法,朴素二叉树、Boost、Prievlet的 O(lb3N)精确度指标分别为1、6、6。其中关于朴素二叉树和Boost算法的O(lb3N)精确度指标的前置分析计算过程在文献[15]中有详细的分析,只需将均方误差按本文方法进一步推导即可得出,这里不再赘述;而Prievlet算法的O(lb3N)精确度指标已于前文中得出。
5 实验分析
本文将通过实验来验证文中提出的求解均方误差的算法以及公式的正确性。本文进行多次实验,对多次实验的误差取平均值作为实验误差。同时通过算法3以及式(17)计算出相对应的理论误差,将两者进行比较,来验证本文理论分析的正确性。
本文实验是在奔腾双核CPU T4200 2.00 GHz的计算机下完成。采用的语言为Matlab,实验中差分隐私参数ε统一设置为1。
5.1 验证任意区间查询误差算法
为了能够体现出实验效果,同时考虑实验需要消耗的时间,本文所采取的数据规模为1 024。随机生成了50个查询区间,分别计算理论上和实验实际产生的均方误差。每个查询区间重复实验100次,将每次所产生的均方误差取平均作为最终的实验结果,而理论误差则通过算法3计算。详细实验结果如表1所示。
为了让读者更加直观地比较理论误差与实验误差,将表1中的数据制作成折线图,如图4所示。
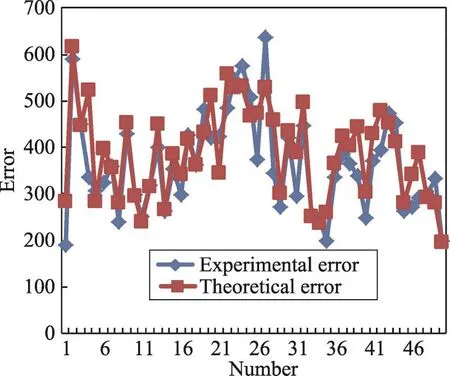
Fig.4 Comparison of experimental error with theoretical error in fixed query interval图4 固定查询区间下实验误差与理论误差的对比图
观察图4可以发现,总体上实验结果与理论结果还是比较接近的,而且实验产生的误差围绕着理论误差上下波动,符合差分隐私所添加噪声是随机的这一特点。此外,表1中,有的查询区间实验结果与理论结果较接近,而有的则相差较大,这说明查询区间的不同产生的误差波动程度不一,这也是由于实验次数不够多,随着实验次数增多,所有的查询区间的误差会与理论误差越来越接近。
5.2 验证平均区间查询误差算法
接下来,将对前文分析得出的Prievlet算法在平均情况下的均方误差进行实验论证。为了更好地验证该理论分析的正确性,本文对所有可能的区间进行实验,最终取平均值作为实验结果。本次实验采用的数据规模为N=2m,0≤m≤10,共10组模拟数据进行实验对比。与上个实验一样,本实验也进行了100次重复实验,之后取平均值作为实验结果,并根据式(17)计算得出理论上的均方误差进行比较。实验结果如表2所示。
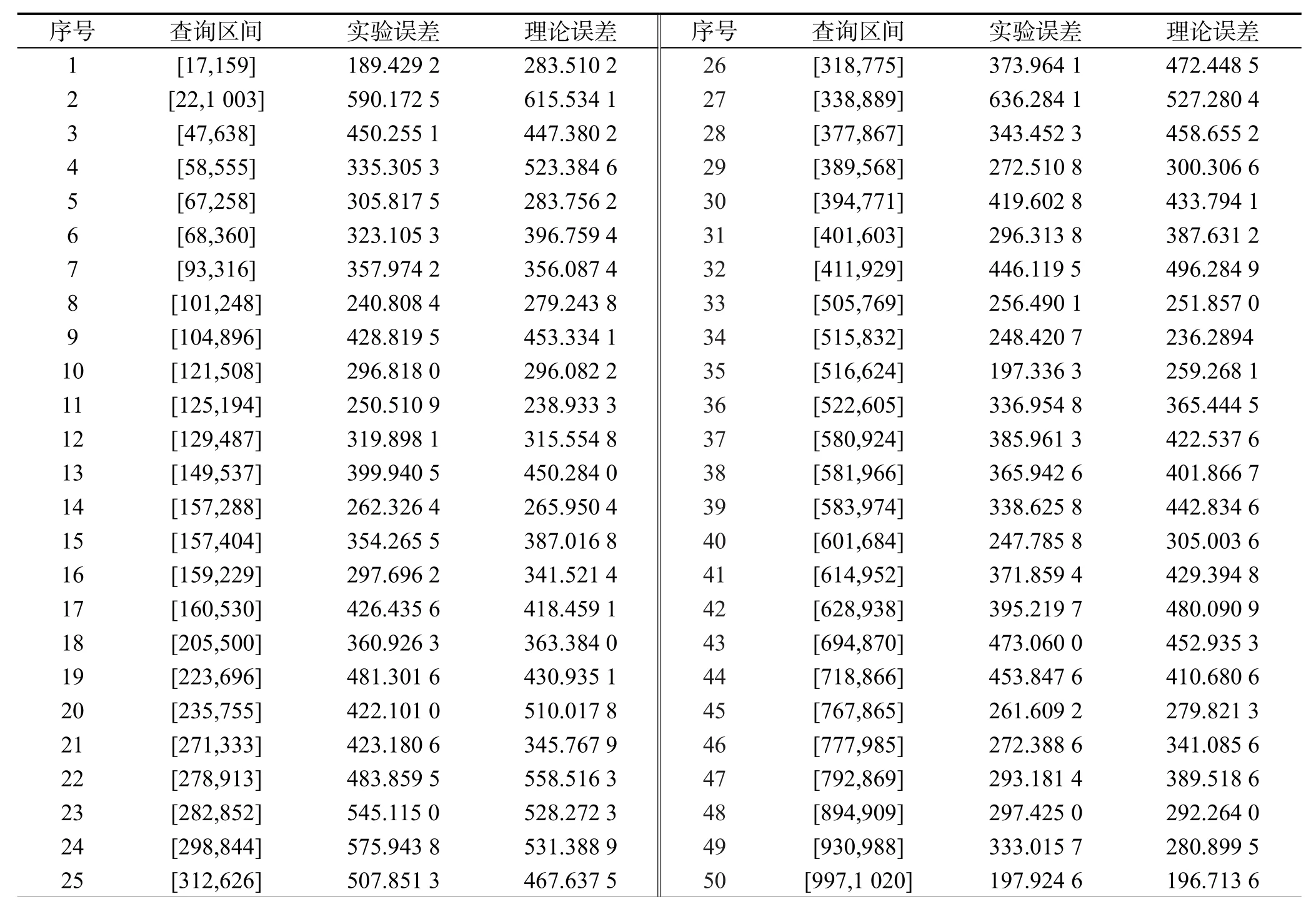
Table 1 Results of two errors in fixed query interval表1 固定区间查询下两种误差的计算结果
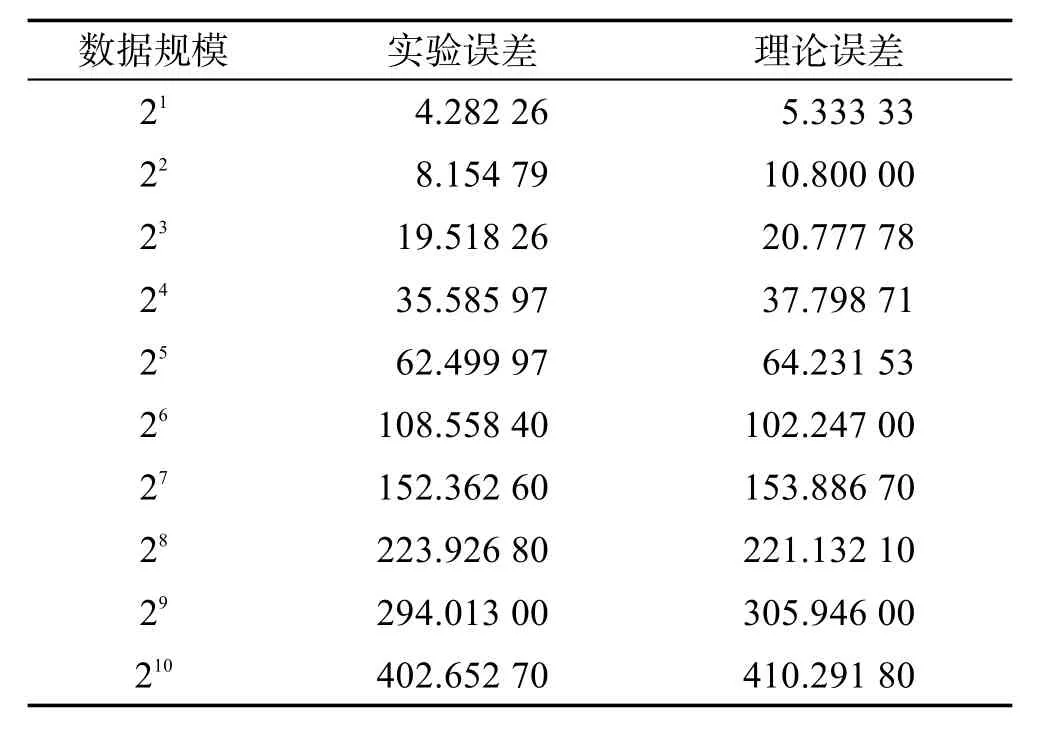
Table 2 Experimental error and theoretical error in mean case表2 平均情况下的实验误差与理论误差
为了方便观察,将实验结果用折线图的方式表示。实验结果如图5所示。
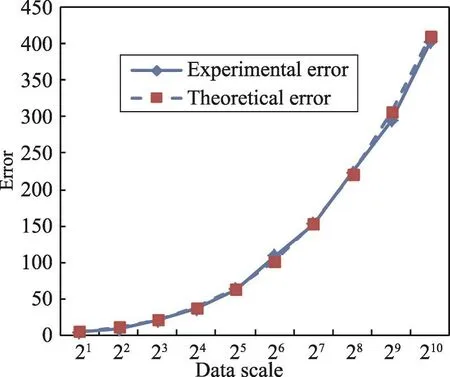
Fig.5 Comparison of experimental results with theoretical results in mean case图5 平均情况下实验误差与理论误差的对比图
从图5可明显地看出,实验结果与分析结果几乎一样,进一步说明了式(17)计算出的Prievlet算法均方误差能准确地反映算法性能,验证了该公式的正确性。
6 结束语
本文利用矩阵机制的相关理论,分析了以Prievlet算法为代表的基于矩阵机制的差分隐私数据发布方法的理论误差,成功求解了Prievlet算法在任意区间查询下的均方误差和平均情况下的均方误差公式。并在此基础上提出了可有效衡量具有相同误差渐进阶的不同差分隐私发布算法之间性能差异的精确度指标。
附录: