常见几何体的内切球与外接球问题
李冬禄
(辽宁省凌源中学 122500)
一、正方体的内切球与外接球
设正方体棱长为a,外接球半径为R,内切球半径为r,则:
结论1: 正方体的外接球半径R为正方体对角线的一半,即:(2R)2=3a2
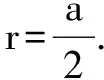
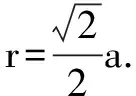
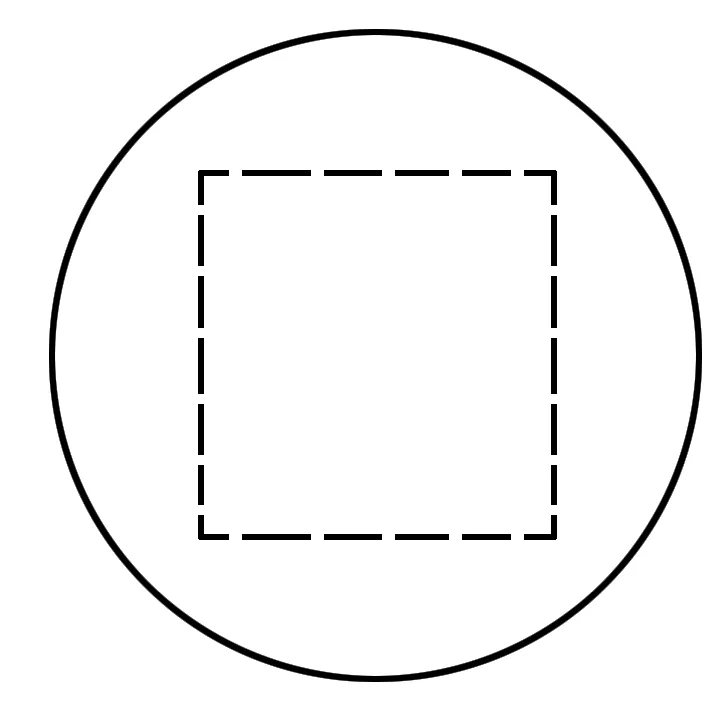
图1
例1(2013福建12) 已知某一多面体内接于球构成一个简单组合体,如果该组合体的正视图、 俯视图均如图1所示,且图中的四边形是边长为2的正方形,则该球的表面积是____.

二、长方体的外接球
设长方体的棱长为a、b、c,外接球半径为R,则:
结论4: 长方体的外接球半径R为体对角线的一半,即:(2R)2=a2+b2+c2.
结论5:三条棱两两垂直、三个侧面两两垂直、对棱相等的三棱锥,其外接球问题均可构造成对应的长方体进行求解.
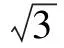
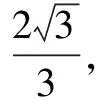
练习:
1. 已知各顶点都在同一个球面上的正四棱柱的高为4,体积为16,则这个球的表面积是(24π).

3.三棱锥A-BCD,其中AB=CD=5,AC=BD=6,AD=BC=7,则该三棱锥外接球的表面积为(55π).
三、正四面体的外接球与内切球
设正四面体棱长为a,外接球半径为R,内切球半径为r,则:
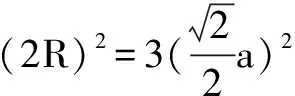

结论7:正四面体的内切球半径可用等积法求解,且R∶r=3∶1(如图3).

例3正四面体的四个顶点都在表面积为36π的球面上,则该四面体的棱长为____.

四、直棱柱的外接球问题
设直棱柱的高为h,底面多边形的半径即外接圆半径为r,外接球半径为R,则:
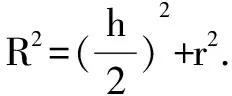
例4(2013辽)已知直三棱柱ABC-A1B1C1的6个顶点都在球O的球面上.若AB=3,AC=4,AB⊥AC,AA1=12,则球O的半径为().

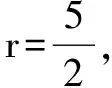
练习:1.(2010新课标)设三棱柱的侧棱垂直于底面,所有棱长都为a,顶点都在一个球面上,则该球的表面积为( B ).
2.(2009全国1)直三棱柱ABC-A1B1C1的各顶点都在同一球面上,AB=AC=AA1=2, ∠BAC=120°,则此球的表面积等于(20π).
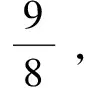
五、特殊棱锥的外接球问题
结论9:若棱锥的顶点可构成共斜边的直角三角形,公共斜边就是其外接球的半径,反之亦成立.
例5 (2012全国)已知三棱锥S-ABC的所有顶点都在球O的球面上,△ABC是边长为1的正三角形,SC为球O的直径,且SC=2,则此棱锥的体积为().
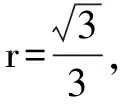
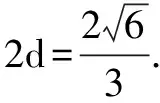
此棱锥的体积为

六、几何体的最值问题
例6 (2010全国1)已知在半径为2的球面上有A、B、C、D四点,若AB=CD=2,则四面体ABCD的体积的最大值为(B).
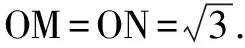
练习:(2015新课标2)已知A,B是球O的球面上两点,∠AOB=90°,C为该球面上的动点,若三棱锥O-ABC体积的最大值为36,则球O的表面积为(C).
A.36πB.64πC.144πD.256π
总之,几何体与球的有关组合问题,是高考的常考考点,如果能熟练掌握常见几何体的外接球与内切球的有关结论,在高考中就会得到事半功倍的效果.

