高速铁路磨耗车轮与60N钢轨静态接触分析

马晓川,　王　平,　王　健,　徐井芒

(1. 西南交通大学高速铁路线路工程教育部重点实验室, 四川 成都 610031; 2. 华东交通大学铁路环境振动与噪声教育部工程研究中心, 江西 南昌 330013)

我国高速铁路的建设过程中,钢轨断面一直采用单一的CHN60轨头廓形,现有的客运车辆及车轮型面种类繁多,例如LMA、S1002CN、XP55、LM等类型的车轮型面与CHN60钢轨接触时导致轮轨关系十分复杂,并引起轮轨接触关系不良,对高速车辆的平稳运行产生不利影响[1-2].为研究这一问题,干锋等[3]针对国内铁路客运车辆的4种典型踏面,计算并给出4种踏面与CHN60的轮轨接触特征,为实际线路车轮磨耗跟踪试验和磨耗行为研究提供了参考.肖广文等[4]比较了不同车轮踏面对高速客车动力学性能的影响,发现要确定合适的车轮踏面,须从车轮与钢轨接触关系出发,综合评估车辆动力学性能.罗仁等[5]研究了4种典型踏面类型对车轮踏面磨耗的影响.中国铁道科学研究院以CHN60钢轨为原型,研究设计出了能够适应不同车轮型面的60N钢轨[1],经理论和试验研究,新建设线路钢轨将采用60N轨头廓形,既有线的钢轨也将参照60N的轨头廓形进行打磨.马晓川等[6]针对60N钢轨与国内客运车辆4种典型踏面的匹配,研究了对车辆直向运行稳定性和曲线通过性能的影响.

高速铁路钢轨采用60N轨头廓形后,既有可能与标准车轮踏面接触,也存在与磨耗车轮踏面接触的可能性,因此,研究磨耗车轮型面与60N钢轨的接触特性是十分必要的.目前,LMA是我国高速铁路车辆常用的车轮型面之一,本文针对不同磨耗程度的LMA车轮型面,从轮轨接触几何关系和非赫兹滚动接触的角度研究与60N钢轨的接触特性,并与CHN60钢轨的计算结果进行对比和分析,为新钢轨的现场使用提供理论依据.

1　车轮与钢轨型面

1.1　磨耗状态下车轮踏面形状

对某既有提速线路上运行250 km/h级别高速列车的车轮型面进行追踪测试[7],分别得到车辆运行5、10、15、20、25 万公里后的车轮踏面形状如图1中所示.

1.2　钢轨轨头廓形

图2为高速铁路60N钢轨与CHN60钢轨的轨头廓形对比.CHN60钢轨的轨头廓形由3段圆弧组成,半径分别为300、80、13 mm,60N钢轨的轨头廓形则由4段圆弧组成,半径分别为200、60、16、8 mm.

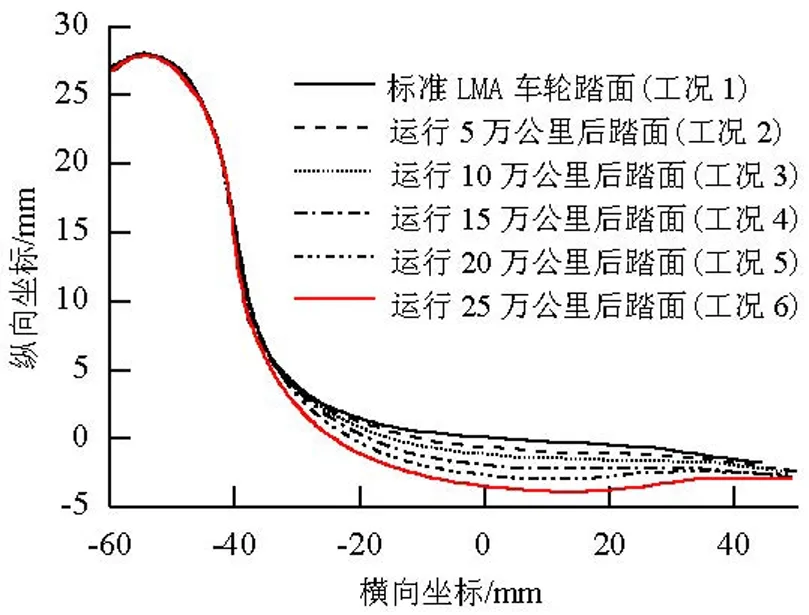
图1　实测车轮形状Fig.1　Measured wheel shape

图2　钢轨廓形对比(虚线为60N,实线为CHN60)Fig.2　Rail profile comparison (dotted line is 60N, and solid line is CHN60)

2　轮轨接触几何关系

根据车轮与钢轨的空间位置约束关系和迹线法的基本原理[8-9],求解不同轮对横移量时轮轨接触点的位置分布,并进一步求解轮对的滚动圆半径以及轮轨接触角等参数；利用计算得到的轮轨接触几何参数,求解滚动接触的轮轨蠕滑率.

轮轨接触几何计算模型的关键参数如下：

钢轨的轨底坡为1/40；

轨距为1 435 mm；

轮背距为1 353 mm；

车轮名义滚动圆半径为430 mm.

2.1　轮轨接触点位置分布

轮轨接触点位置对轮轨磨耗位置及车辆动力学性能等具有重要影响[10].接触点位置分布过于集中时,会导致轮轨磨耗过于集中,当接触点位置分布过于分散时,降低车辆直向运行的稳定性.不同磨耗程度的车轮踏面与CHN60钢轨接触时,其接触点位置的分布如图3所示.轮对横向位移取-12～12 mm,计算步长为0.5 mm[11].不同磨耗程度的车轮踏面与60N钢轨接触时,接触点位置的分布如图4所示.轮对横向位移取-12～12 mm,计算步长同样取0.5 mm.对于标准的LMA车轮踏面,其轮轨接触点位置主要分布在钢轨的轨顶中心位置处,且接触点的分布较为集中,而对于磨耗状态的车轮,轮轨接触点的位置开始向两侧扩散,分布较为分散.接触点位置在钢轨轨顶和轨距角两个区域之间存在跳跃的可能性,造成轮轨接触关系不良,导致车辆运行稳定性降低.

(a) 标准车轮踏面LMA(b) 运行5 万公里后踏面(c) 运行10 万公里后踏面(d) 运行15 万公里后踏面(e) 运行20 万公里后踏面(f) 运行25 万公里后踏面图3 轮轨接触点位置分布(CHN60)Fig.3 Distribution of wheel-rail contact points (CHN60)

(a) 标准车轮踏面LMA(b) 运行5 万公里后踏面(c) 运行10 万公里后踏面(d) 运行15 万公里后踏面(e) 运行20 万公里后踏面(f) 运行25 万公里后踏面图4 轮轨接触点位置分布(60N)Fig.4 Distribution of wheel-rail contact points (60N)

定义车轮和钢轨上接触点的横向分布宽度如式(1),该参数可在一定程度上表征轮轨接触点位置的变化幅度.

lyW,R=YmaxW,R-YminW,R,

(1)

式中:下标W、R分别代表车轮或钢轨;

YmaxW,R为接触点横向坐标的最大值;

YminW,R为接触点横向坐标的最小值.

车辆在直线轨道上运行时,轮对的动态横移量基本符合正态分布的规律,该正态分布的数学期望为0,标准差为4,轮对横移在4 mm以内发生的概率最大[12].计算轮对横移在-4～4 mm范围内,车轮上接触点横向分布宽度随车辆运行里程的变化规律如图5所示.

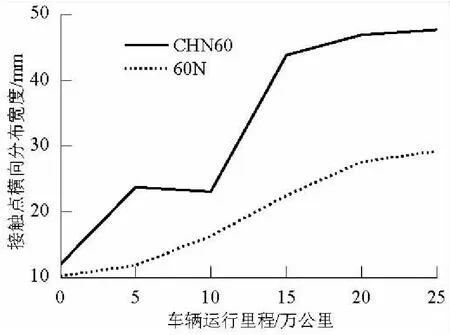
图5　轮轨接触点横向分布宽度(车轮)Fig.5　Lateral distribution width of wheel-rail contact points (wheel)

随车辆运行里程的增加,车轮上接触点的横向分布宽度随之增大,接触点的横向分布宽度越大,表明车辆动态运行时,轮轨接触点位置的变化幅度越大,不利于车辆的平稳运行.

由图5可见,60N钢轨的轮轨接触点横向分布宽度小于CHN60钢轨,说明在相同条件下,60N钢轨对应的车辆运行稳定性较好.车辆运行25 万公里后,60N钢轨对应的轮轨接触点横向分布宽度为29.2 mm,CHN60钢轨对应的轮轨接触点横向分布宽度为47.7 mm,约为60N钢轨的2倍.60N钢轨的轮轨接触点横向分布宽度相对较小,在相同条件下会加速车轮踏面的凹槽磨耗.但在高速铁路中,为提升旅客的乘坐舒适性,要求车辆的运行能够尽可能的平稳;另一方面,由于车辆的轴重普遍较小,车辆运行稳定性引起的滚动接触疲劳是引起轮轨伤损的主要原因.因此,60N钢轨的设计初衷就是提升高速车辆的运行稳定性,从而提升旅客的乘坐舒适性、减少轮轨伤损,并降低养护维修工作量.

2.2　滚动圆半径差

左右车轮滚动圆半径差对车辆的动力学性能有十分重要的影响,较小的滚动圆半径差有利于轮对直向运行稳定性,较大的滚动圆半径差有利于提高轮对通过小半径曲线的能力.高速铁路大多为直线或大半径曲线线路,降低轮对滚动圆半径差有利于提高车辆高速运行下的稳定性.不同磨耗程度车轮踏面与CHN60、60N钢轨接触时,滚动圆半径差随轮对横移量的变化规律如图6.随车轮型面磨耗程度的加大,2种钢轨对应左右车轮的滚动圆半径差均随之增大.

由图6可见,与60N钢轨相比,CHN60钢轨的滚动圆半径差变化幅度较大,以车辆运行25 万公里的工况进行说明,60N钢轨在轮对横移大于7 mm时,轮轨接触点位置向钢轨轨距角位置移动,左右车轮滚动圆半径差出现较大程度的增大,CHN60钢轨在轮对横移大于3 mm时,左右车轮滚动圆半径差出现较大程度的增大.

(a) CHN60钢轨

(b) 60N钢轨图6　轮对滚动圆半径差随轮对横移量的变化规律Fig.6　Rolling radii difference vs. lateral displacement of wheel set

3　三维非赫兹滚动接触

Kalker利用连续介质力学的虚功原理及其对偶形式,推导并提出了三维弹性体非赫兹滚动接触理论,在这一理论的基础上,通过编制FORTRAN语言形成了数值程序,名为CONTACT[13-14],这一理论是目前为止世界上最为精确的轮轨滚动接触求解方法,能够在满足假设条件下,计算任意轮轨廓形接触条件下的滚动接触信息.

本文将采用数值程序CONTACT来求解轮轨滚动接触过程中接触斑、轮轨磨耗指数、滚动接触疲劳因子等随磨耗车轮型面及轮对横移的变化规律.轮轨滚动接触模型中的关键计算参数为:轮对轴重取14 t(CRH2型车),轮轨材料的剪切弹性模量取82 GPa,材料泊松比为0.28,轮轨静摩擦因数和动摩擦因数分别取0.30和0.29,车轮滚动速度取250 km/h.

3.1　接触斑面积

轮轨接触斑面积越大,在相同法向轮轨力的作用下,其法向接触应力越小,法向接触应力是影响轮轨磨耗和接触疲劳的重要因素.图7为不同磨耗程度的车轮踏面与CHN60、60N钢轨接触时,轮轨接触斑面积随轮对横移的变化规律.

(a) CHN60钢轨

(b) 60N钢轨图7　接触斑面积随轮对横移量的变化规律Fig.7　Wheel-rail contact area vs. lateral displacement of wheel set

当车轮轮缘贴靠钢轨时(轮对横移量大于10 mm),轮轨接触斑面积急剧缩小,这也是导致轮轨法向接触应力急剧增大的主要原因.与60N钢轨相比,CHN60钢轨对应的轮轨接触斑面积的变化规律较为杂乱,对于工况4、5、6,当轮对横移超过4 mm时,轮轨接触斑面积急剧降低,由100 mm2降低到了30 mm2左右,原因是车轮开始与钢轨的轨距角位置接触,轮轨廓形的相对曲率较大,造成轮轨接触斑面积较小,同样条件下会引发较大的轮轨法向接触应力,不利于钢轨磨耗、疲劳等伤损.接触斑面积变化规律与车辆运行里程之间呈现出非线性的关系.

3.2　磨耗指数

车轮与钢轨滚动接触时,轮轨蠕滑力是引起轮轨磨耗的主要原因,切向蠕滑力过大时,将加速车轮和钢轨材料的磨耗速率.轮轨磨耗指数的计算方法及各个参数代表的含义见文献[6]中式(1).

图8为不同车辆运行里程车轮型面与CHN60、60N钢轨接触时,轮轨磨耗指数的变化规律.由图8可知,磨耗车轮踏面对应的轮轨磨耗指数普遍偏大,随磨耗程度的增大,轮轨磨耗指数逐渐增大.相比60N钢轨,CHN60钢轨对应的轮轨磨耗指数普遍偏大,不利于轮轨廓形的保持能力.

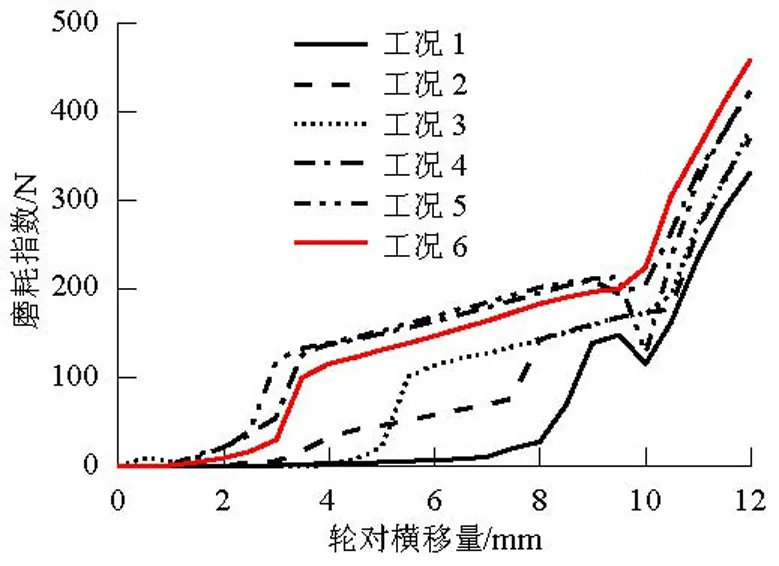
(a) CHN60钢轨

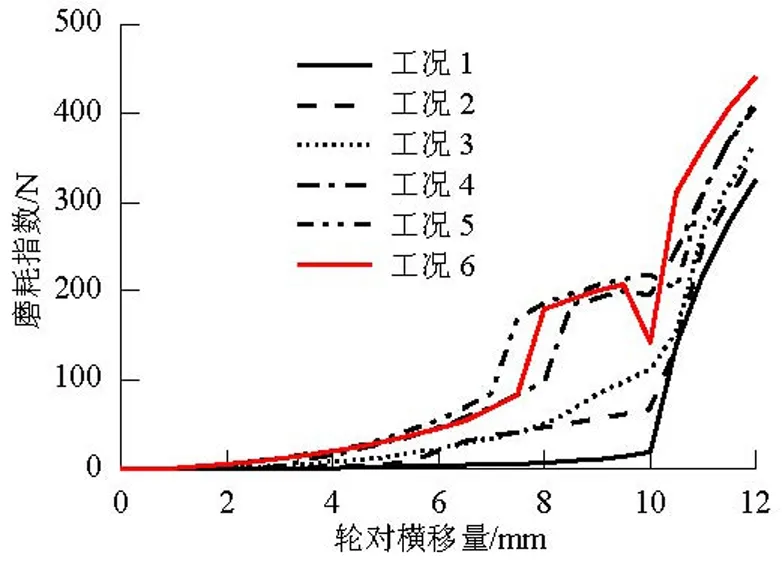
(b) 60N钢轨图8　轮轨磨耗指数随轮对横移量的变化规律Fig.8　Wheel-rail wear index vs. lateral displacement of wheel set

3.3　滚动接触疲劳因子

表面滚动接触疲劳因子的计算方法见文献[15]中式(4).当疲劳因子大于0时,说明作用切向应力大于材料剪切屈服强度,进入疲劳区.图9为不同运行里程磨耗车轮与两种钢轨接触时表面滚动接触疲劳因子随轮对横移的变化规律.

对于标准的LMA车轮踏面,其对应的轮轨表面滚动接触疲劳因子较小,磨耗后的车轮踏面,滚动接触疲劳因子大于0的情况居多,并且随着车辆运行里程的增大,位于表面滚动接触疲劳区的范围越来越大.相比60N钢轨,CHN60钢轨表面滚动接触疲劳因子大于0的情况居多,表明在相同条件下,CHN60钢轨更容易发生滚动接触疲劳伤损.

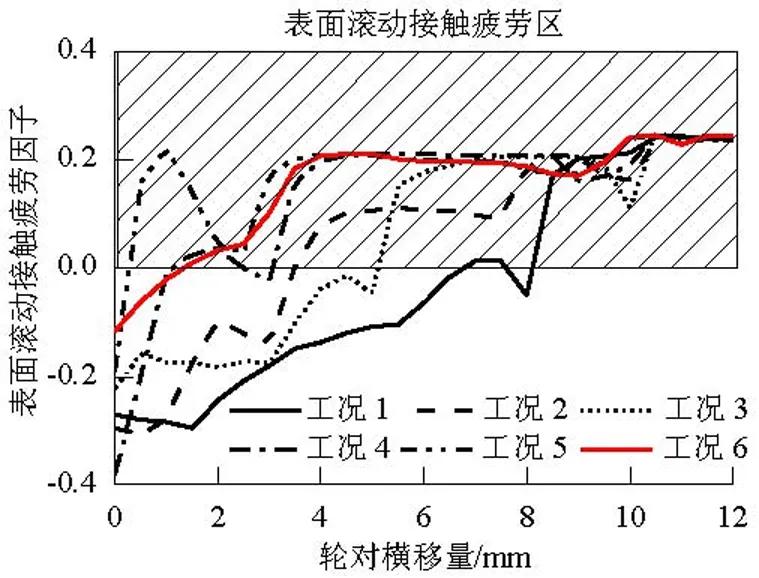
(a) CHN60钢轨

(b) 60N钢轨图9　表面滚动接触疲劳因子随轮对横移量的变化规律Fig.9　Surface rolling contact fatigue index vs. lateral displacement of wheel set

4　结　论

本文从轮轨静态接触几何参数和非赫兹滚动接触两方面,分析了不同车辆运行里程后磨耗车轮型面与60N钢轨的静态接触特性,并与CHN60钢轨的计算结果进行了对比,得到如下结果:

(1) 随车辆运行里程的增加,车轮上接触点的横向分布宽度随之增大.60N钢轨的轮轨接触点横向分布宽度明显小于CHN60钢轨,即在相同条件下,60N钢轨对应的车辆运行稳定性较好.

(2) 随车轮磨耗程度的加大,左右车轮的滚动圆半径差随之增大.60N钢轨的滚动圆半径差变化幅度较小,在相同条件下,有利于车辆的高速运行稳定性.

(3) 磨耗车轮的轮轨磨耗指数普遍偏大,且随磨耗程度的增大,轮轨磨耗指数逐渐增大.60N钢轨的轮轨磨耗指数普遍较小,有利于轮轨廓形的保持能力.

(4) 标准LMA车轮对应的轮轨表面滚动接触疲劳因子较小,磨耗车轮滚动接触疲劳因子大于0的情况居多,并且随着车辆运行里程的增大,位于表面滚动接触疲劳区的范围越来越大.相比CHN60钢轨,60N钢轨表面滚动接触疲劳因子大于0的情况较少,在相同条件下,能够减少滚动接触疲劳伤损的发生.

本文仅从静态接触的角度对磨耗车轮型面与CHN60、60N钢轨接触时的影响进行了详细分析,后续将从车辆轨道动力学的角度出发,研究磨耗车轮对车辆动态运行时轮轨动力相互作用的影响.