铁路大跨T形刚构桥车桥耦合振动与动力性能
勾红叶, 石晓宇, 周 文, 康 锐
(西南交通大学土木工程学院, 四川 成都 610031)
列车以一定速度通过桥梁时,由于列车轴重、轨道不平顺和轮对蛇形运动等因素,会引起列车和桥梁的耦合振动.由列车作用引起的桥梁结构振动,不仅会影响桥上行车的安全性和平稳性,还会增大桥梁结构的内力,引起桥梁结构的局部疲劳损伤,甚至导致桥梁的破坏.随着铁路重载化、高速化的发展,车桥耦合振动问题也日益突出[1].
近些年来,随着车桥计算理论及计算机技术的发展,对桥梁模型的研究从中小跨径的简单桥梁向各种大跨度、形式复杂的桥梁进行了开展:崔圣爱等[2-3]利用多体系统动力学软件SIMPACK建立车辆模型,采用有限元软件ANSYS建立桥梁模型,通过SIMPACK与ANSYS的联合仿真,研究了大跨连续梁桥及钢桁斜拉桥的车桥耦合振动特性,探讨了列车速度对车辆的安全、舒适性指标以及桥梁结构竖、横向位移及加速度的影响;李永乐等[4]基于风-车-桥系统空间耦合动力学模型,研究了公铁两用大跨度悬索桥的结构动力特性及风-车-桥耦合振动性能,对比分析了不同风速条件下桥梁结构动力响应的变化;孙耀等[5]基于车桥耦合振动理论,研究了钢管混凝土系杆拱桥在车辆荷载作用下的动力效应,分析了车速、车重以及不平顺等级等因素对拱肋、吊杆、桥面跨中等关键部位动力响应的影响;王彪等[6]采用多刚体动力学理论及模态综合法建立了列车-曲线桥梁耦合振动分析模型,研究了客货共线铁路列车车辆通过曲线梁桥时的动力响应随曲线半径、缓和曲线长度及曲线外轨超高等因素的变化规律,并基于列车走行的安全性提出了曲线半径的限值;卫星等[7]基于车桥耦合振动分析和实桥动载试验,研究了连续刚构桥的车桥耦合振动特性与动力性能.除此之外,众多学者还对形式复杂的组合体系桥梁、钢混组合梁桥及桥上道岔区间的车桥耦合振动进行了探讨研究[8-12].已有研究涉及拱桥、斜拉桥、悬索桥、连续刚构桥等多种桥型,但对铁路大跨T形刚构桥的研究却相对匮乏.同时,多数研究集中于车桥耦合振动理论计算,结合实桥动载试验对桥梁结构进行综合评判的研究相对较少,因此有必要基于车桥耦合振动理论计算和实桥动载试验对该类型桥梁的动力特性进行研究.
本文通过车桥耦合振动理论计算和实桥动载试验相结合的方法对铁路大跨T形刚构桥动力性能进行详细分析.通过车桥耦合振动计算,深入分析车辆的各项动力学指标与列车的走行安全性和平稳性;基于实桥动载试验,准确获得桥梁结构实际的模态参数及振动响应,以了解该类桥梁的自振特性和动力性能,检验桥梁在不同列车运行速度下的实际工作状态,测量在货车移动荷载作用下桥跨结构的动挠度、控制截面的动应变、横向、竖向振幅及加速度,分析评价桥梁的动力系数和桥梁的竖、横向刚度是否满足有关要求.可为该类铁路桥梁的运营管理与养护维修累积相关资料,同时也为同类型桥梁的结构设计提供相关依据.
宜万铁路马水河大桥是我国首座铁路大跨T形刚构桥,其主桥为116.8 m+116.8 m的T形刚构,桥梁全长281.66 m.梁部混凝土采用C60,主梁横截面为单箱单室截面,箱梁顶板宽为10.70 m,底宽为6.00 m,道碴槽宽为8.40 m.采用双线I级铁路设计,线间距为4.20 m,左线为正线,设计荷载为中-活荷载.马水河大桥见图1所示.
1 车桥耦合振动分析
车桥耦合振动模型由车辆和桥梁两个动力学模型组成,二者通过轮对与钢轨间的相互作用相联系.一般而言,以刚体动力学方法建立车辆动力学模型,以有限元方法建立桥梁动力学模型[2].
1.1 车辆动力学模型
铁路车辆由车体、转向架、轮对等基本部件组成,为复杂的多自由度体系,为尽可能准确地得到车辆的动力响应以分析其车桥耦合振动特性,本文车辆模型采用空间车辆模型,将车体、转向架及轮对等基本部件视为刚体,通过一系悬挂装置连接.车辆动力学模型中,车体及单个转向架考虑浮沉、横摆、侧滚、摇头、点头等5个自由度;单个轮对考虑浮沉、横摆、侧滚、摇头等4个自由度,故整个车辆模型共31个自由度.取坐标系统如图2所示.图中:x为纵向位移;z为竖向位移;y为横向位移;φ为侧滚转角;ψ为摇头转角;θ为点头转角.

图2 坐标系统简图Fig.2 Coordinate system diagram
于是车体自由度为
Uc=[zcycφcψcθc]T;
(1)
转向架自由度为
Utj=[ztjytjφtjψtjθtj]T,j=1,2;
(2)
轮对自由度为
Uωi=[zωiyωiφωiψωiθωi]T,i=1,2,3,4.
(3)
根据D’Alembert原理,可推导出车辆系统的运动微分方程,详细可参考文献[13]中车辆运动微分方程相关部分.基于车辆各刚体的平衡方程,形成矩阵形式为

(4)
式中:M为车辆系统的质量矩阵,包含车体、转向架以及轮对3个子系统的质量矩阵,通过组装而成,其中:下标c代表车体;下标t代表转向架;下标ω代表轮对,如下:
M=
(5)
K为车辆系统的刚度矩阵,
K=

(6)
C为车辆系统的阻尼矩阵,其形式与刚度矩阵相同;
F为车辆所受荷载列阵,包含了轨道结构对轮对的作用力以及车辆所受的除轮对力之外的其他外力,表示为
F=[FcFt1Ft2Fω1Fω2Fω3Fω4]T;
(7)
X为车辆系统的位移,由各刚体在各自由度上的运动位移组装而成:
X=[XcXt1Xt2Xω1Xω1Xω3Xω4]T.
(8)
1.2 桥梁动力学模型
采用有限元方法对桥梁进行分析,利用空间杆系单元建立用于车桥耦合振动分析的桥梁结构模型,见图3.本桥为T形刚构桥梁,墩梁固结;梁端处约束梁体节点的横向、竖向相对位移和绕桥轴线的相对转角.桥梁结构的振动微分方程为
(9)
式中:M1、K1分别为桥梁结构的质量矩阵和刚度矩阵;X1为桥梁节点的位移向量;F1为作用在桥梁上的节点力向量;C1为桥梁结构的阻尼矩阵,这里采取瑞利阻尼:
(10)
式中:ξ为阻尼比;ω1、ω2为桥梁的任意两阶圆频率,一般取前两阶整体振型相应的圆频率.

图3 桥梁有限元模型Fig.3 Finite element model of the bridge
1.3 车桥相互作用
车桥耦合振动分析中,车辆模型与桥梁模型通过轮轨接触关系相互联系,考虑法向上的Hertz非线性弹性接触理论和切向上的Kalker蠕滑理论.根据轮轨间作用力平衡条件及变形协调条件,可建立车桥耦合振动方程为
(11)
马水河大桥车桥耦合振动分析中,列车荷载由C62货车车辆充当,编组为:DF4机车+9辆C62货车.C62货车采用转8A转向架,该转向架的设计构造速度为80 km/h,计算和试验均表明,车速超过80 km/h时的桥梁振动偏大,其主要原因在于车辆达到了动力失稳车速,车辆本身的振动过大所致,因此不应作为控制桥梁设计的工况,而新型货物列车运行120~130 km/h时的振动响应比转8A货车运行60~70 km/h时要小[14],故采用C62货车编组计算是偏于安全的.中国铁路货车的保有量中转8A转向架车辆也占相当大的比重,该计算条件与桥梁的实际运用情况也是相符的.计算车速采用40、50、60、70、80 km/h和90 km/h,每级速度分列车单线行车和双线对开两种开行工况.以轨道不平顺车作为车桥耦合系统的激励源,轨道不平顺通过美国六级谱拟合,采用Newmark-β法求解.
1.4 车桥耦合振动分析结果
基于车桥耦合振动理论分析,不同车速列车过桥时车辆响应见表1.
由表1可以看出:除车辆横向加速度以外,其他各项动力学指标均随车速的提高而增大;车辆脱轨系数和轮重减载率的最大值分别为0.30和0.39,满足相关规范[15]脱轨系数小于0.8,轮重减载率小于 0.6 的要求;最大轮轴横向力为38.15 kN,小于规范[16]限值的80 kN,说明列车在桥上运行时具有良好的安全性.依据相关规范[16],车辆横向加速度均小于5.0 m/s2,竖向加速度均小于7.0 m/s2,结合平稳性指标综合评判,列车的平稳性等级为“优良”,表明列车在桥上运行时具有良好的平稳性.

表1 列车过桥时车辆响应Tab.1 Dynamic responses of carriages under the train running on the bridge
2 动载试验内容与测点布置
对马水河大桥进行动力荷载试验,包括脉动试验、行车试验及制动试验3个部分.通过脉动试验测得桥跨结构的固有频率、振型及阻尼比,得到桥跨结构的自振特性;由行车试验及制动试验测试列车动荷载作用下的动应变、动力系数、加速度、动挠度及横向振幅等动力响应.行车试验采用单线开行和双线对开两种方式,行车速度的选择包括5(标定车速试验)、20、40、60、80 km/h;制动试验的制动车速选择为40 km/h;行车试验和制动试验的动力荷载均由1HXD3/1HXD3C机车+14C62AT/C62BK/C64T/C64K/C70+1HXD3/1HDX3C机车组成.
动应力测试截面位置见图4,各测试截面顶板下缘与底板上缘各对称布置2个动应变测点,全桥共2个动力测试截面,即图中A-A截面和B-B截面,共计8个动应变测点.
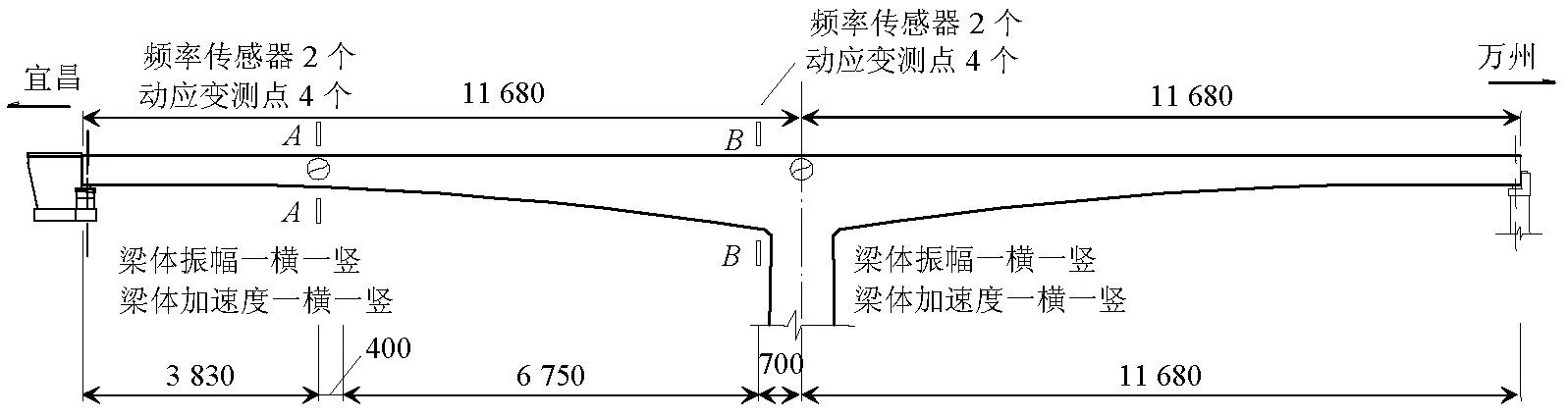
图4 马水河大桥动载试验测试截面布置示意图(单位:cm)Fig.4 Positions of measured sections and arrangement of measuring points (unit: cm)
3 动载试验结果与分析
3.1 自振特性分析
动载试验中采用脉动法测试自振频率.通过对脉动信号及列车过桥后的余振波形进行谱分析,得到桥梁的自振频率及阻尼比,桥梁自振特性测试结果见表2.
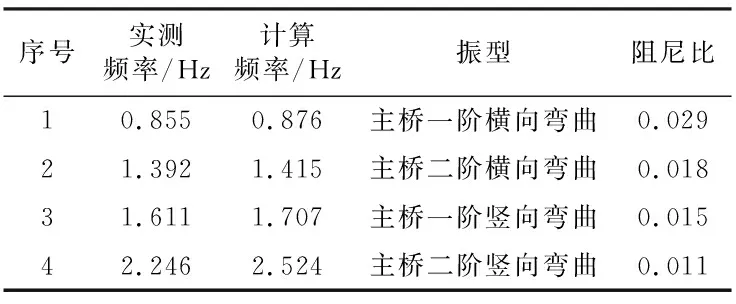
表2 桥梁自振特性Tab.2 Free-vibration characteristics of the bridge
从实测结果与计算结果对比可以看出,主桥一、二阶横向弯曲和一、二阶竖向弯曲频率吻合良好,略低于计算值.对比实测与计算振型图也可看出,二者振型符合较好,明确地反映了桥跨结构横、竖向一阶振型状况,且符合动力学基本原理,从而验证了有限元模型的有效性.实测横向基频大于相应规范[17]中所规定的限值f=90/L=0.388 Hz,其中,L为桥梁跨度,可认为桥跨结构具有良好的横向刚度.实测桥跨结构的阻尼比在0.011~0.029之间,符合实际情况.
3.2 动应变与动力系数
试验列车以不同的速度通过桥梁时各测试截面的动力系数见表3.
从表3可以看出,车桥耦合振动计算结果与实测结果符合较好.主梁边跨控制截面A-A各测点的实测应变动力系数介于1.01~1.07之间;主梁墩顶附近截面B-B各测点的实测应变动力系数介于 1.00~1.08之间;动力系数随速度的增加变化并不明显.在40 km/h行车制动时,各控制截面动力系数最大值分别为1.07和1.08,动力系数相对较小,可见列车制动对桥跨结构的动力效应并不明显.
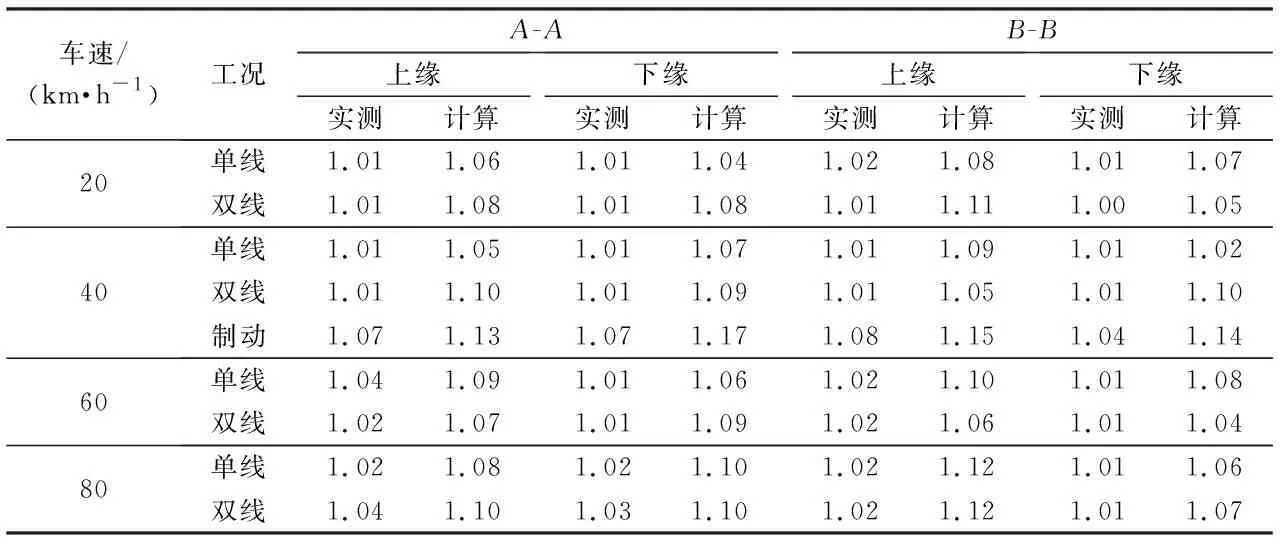
表3 控制截面处动力系数Tab.3 Dynamic coefficients of control sections
3.3 加速度
图5~6分别给出了单线80 km/h行车工况下A-A截面竖向加速度和B-B截面横向加速度的实测及计算时程曲线.不同车速下A-A截面和B-B截面振动加速度的实测及车桥耦合振动计算最大值见表4.
由图5~6及表4可见:测试截面的振动加速度实测值与计算值存在差异,主要原因为实桥轨道不平顺与车桥耦合计算不同,计算采用的轨道不平顺是通过美国六级谱拟合所得,而非实测轨道不平顺;从总体上看,二者变化规律符合较好,车桥耦合计算模型安全可靠;单、双线行车试验中,A-A截面实测竖向加速度最大值分别为0.46 m/s2和0.58 m/s2;除个别值外,在双向交汇行车情况下的横、竖向加速度均大于单线行车的情况,表明双线交汇行车时桥梁横竖向振动比单向行车时要大;列车制动引起桥梁结构各方向加速度均较小,表明列车制动对桥梁结构振动加速度影响较小.B-B截面由于位于桥墩附近,故振动加速度相对较小;在双线行车速度为80 km/h时,A-A截面附近实测横向加速度达到最大值0.27 m/s2,远小于检定规范[17]对于横向加速度所要求的限值1.4 m/s2,表明桥跨结构具有良好的横向动力性能.

图5 A-A测试截面竖向加速度时程曲线(单线80 km/h)Fig.5 Time-history curve of measured vertical acceleration at section A-A under the train running on a single line at 80 km/h

图6 B-B测试截面横向加速度时程曲线(单线80 km/h)Fig.6 Time-history curve of measured transverse acceleration at section B-B under the train running on a single line at 80 km/h

车速/(km·h-1)工况A-A横向实测计算竖向实测计算B-B横向实测计算纵向实测计算20单线0.100.190.130.300.030.110.010.09双线0.100.220.210.350.030.150.010.0540单线0.140.240.450.610.030.170.020.10双线0.180.260.360.570.030.140.030.13制动0.070.150.070.240.020.160.030.1560单线0.260.380.430.670.040.200.020.15双线0.240.410.490.650.050.210.030.1280单线0.230.370.460.740.040.270.040.17双线0.270.450.580.780.050.310.040.19
3.4 动挠度及横向振幅
图7~8分别给出了单线80 km/h行车工况下A-A截面动挠度和B-B截面横向振幅的实测及计算时程曲线.表5给出了不同车速下A-A截面横向振幅与动挠度以及B-B截面实测横向振幅的实测值与计算值.
由图7~8及表5可以发现:实测值与计算值变化规律符合较好,计算值大于实测值;测试截面A-A与B-B的横向振幅随车速变化无明显规律;实测A-A截面桥面处横向最大振幅为0.54 mm,小于规范[15]规定限值25.78 mm,满足要求;在双线行车速度为40 km/h时,实测中间墩墩顶横向最大振幅为0.19 mm,小于规范[17]对于高墩桥梁墩顶位移的规定限值5.47 mm,同样满足要求,表明马水河大桥的横向刚度较好.
由A-A截面动挠度实测结果可以看出:A-A测试截面动挠度随车速的增加而增大;在测试工况下,其最大动挠度达到45.5 mm,此时挠跨比为45.5/116 000=3.92×10-4,小于检定规范[17]所要求的限值1/1 300≈7.69×10-4,表明桥跨结构竖向刚度良好.

图7 A-A测试截面动挠度时程曲线(单线80 km/h)Fig.7 Time-history curve of measured and calculated vertical deflection at section A-A under the train running on a single line at 80 km/h
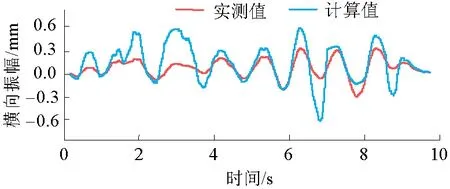
图8 B-B测试截面横向振幅时程曲线(单线80 km/h)Fig.8 Time-history curve of measured and calculated lateral displacement at section B-B under the train running on a single line at 80 km/h

车速/(km·h-1)工况A-A横向振幅实测计算动挠度实测计算B-B横向振幅实测计算20单线0.280.61——0.140.27双线0.310.5739.456.30.100.2540单线0.330.78——0.170.35双线0310.6741.365.80.190.4260单线0.440.84——0.130.25双线0.470.9143.770.20.180.6880单线0.270.75——0.120.31双线0.541.5145.578.60.170.57
4 结 论
(1) 车桥耦合振动分析表明,列车通过桥梁时,车辆的各项动力学指标均随列车速度的提高而增大,其脱轨系数,轮重减载率、轮轴横向力、振动加速度等动力响应值均较小,列车在桥上运行时具有良好的安全性与平稳性.
(2) 宜万马水河大桥桥跨结构实测横向和竖向基频为0.855 Hz和1.611 Hz,计算值与实测值基本符合,桥跨结构具有较大的横向刚度.
(3) 在各速度行车和制动试验工况下,动应变及动力系数均较小,主梁边跨控制截面动力系数最大值为1.07,主梁墩顶附近截面动力系数最大值为1.08,表明桥跨结构受行车及制动的动力作用并不明显.
(4) 试验列车作用下,桥跨结构控制截面横、竖向加速度和横、竖向振幅整体水平较低,满足规范要求,表明桥梁结构具有良好的横向及竖向刚度和动力性能.其中当列车以80 km/h双向对开过桥时,横、竖向加速度达最大值,分别为0.27 m/s2和0.58 m/s2;横、竖向振幅也达最大值,分别为0.54 mm和45.50 mm.

