初始挠度缺陷圆柱形扁壳颤振临界动压研究

范晨光,　杨翊仁

(西南交通大学力学与工程学院, 四川 成都 610031)

薄壳作为一类常见的超声速飞行器结构,在制造工艺流程中或服役阶段会出现几何或物理上的缺陷.初始几何缺陷主要是指制造和装配过程中产生的加工误差、焊接残余变形等初始挠度.对于近空间高速飞行薄壳而言,由于其恶劣的服役环境,初始缺陷可能会对结构的安全性和耐久性产生严重的影响,导致其在远低于临界动压的情况下颤振失稳,并由此带来灾难性后果.

通常情况下,在材料尚未达到屈服强度前,薄壳会在静力或动力荷载作用下破坏,这种破坏呈现强烈的突然性,失稳的形式主要包括屈曲和颤振.由于初始缺陷的存在,这类结构可能会在低于其临界失稳速度的设计值时产生破坏.很早人们发现含有初始缺陷的薄壳其产生屈曲破坏的临界荷载要比不含初始缺陷的薄壳低得多,并开始重视薄壳稳定性对初始缺陷的敏感度问题.Koiter的研究表明[1-2],在薄壳存在初始挠度情况下,受轴压的圆柱壳和与外压下的球壳均有较大的缺陷敏感度.Arboz等[3]研究了圆柱壳地震载荷作用的缺陷敏感度问题,得到了与Koiter相似的结论.Simitses[4]综述了更多的圆柱壳稳定性缺陷敏感度问题,收集了129篇参考文献,详细阐述了缺陷圆柱壳的屈曲和后屈曲问题,涉及的缺陷主要有初始几何缺陷、载荷偏心、材料或结构缺陷.国内在薄壳初始缺陷敏感度问题上的研究也很多,沈惠申等[5]建立了圆柱薄壳外压作用下的边界层理论,同时考虑了前屈曲非线性,大挠度和初始几何缺陷.杜启端[6]对此做了较为全面的综述.

与薄壳屈曲问题一样,在薄壳气动弹性力学问题上,也是由于理论预测的线性系统颤振临界动压与实验结果的显著差异,促使研究者产生了对薄壳初始缺陷敏感度的研究动机.最早在薄壳气动弹性力学问题上考虑初始缺陷影响的是Barr等[7]研究的模型为大挠度完全圆柱壳,缺陷类型为轴对称挠度缺陷.他们的研究表明,初始挠度缺陷会严重影响圆柱壳的颤振特性,使其更加容易失稳.Amabili等[8]研究了轴对称和非轴对称两种初始挠度缺陷类型对圆柱壳气动弹性问题的影响,结果表明,圆柱壳颤振临界动压对初始挠度缺陷的敏感性很大,会因存在缺陷而降低.近年来,在与圆柱壳气动弹性系统相似的输流圆柱壳动力系统中,也开始注重研究初始缺陷对其运动稳定性的影响,Amabili[9-10]和Prado[11]等的研究一致表明,初始挠度缺陷对系统的稳定性会产生不利影响,使其更加容易失稳.目前国内还未开展这方面的研究.

综上所述,对于含有初始挠度缺陷的各向同性完全圆柱壳的流固耦合振动及气动弹性问题,目前研究较少,对于其它类型的薄壳结构,特别是含有初始挠度缺陷的圆柱形扁壳的气动弹性问题,目前尚未有研究涉及.

1　圆柱形扁壳的气动弹性运动方程

假设圆柱形扁壳的初始径向位移(初挠度)为w0,该初始挠度并不引起应力的变化.那么,不考虑非线性项时,带有初挠度的圆柱形扁壳的线性小挠度运动方程为[8-14]

(1)

式中:D=Eh3/12(1-ν2)为弯曲刚度;

E为杨氏模量;

ν为泊松比;

ρ为材料密度;

t为时间变量;

h为壳的厚度;

w为法向位移,以向外为正;

w0为法向初始位移；

f为Airy应力函数;

qγ为法向外力;

R为半径;

x为轴向坐标;

θ为周向坐标；

考虑四边简支的圆柱形扁壳,其边界条件为

(2)

式中:L为轴向长度;

θ0为周向角；

v、u分别为周向和轴向位移.

在此将u=0和v=0写为

(3)

式中:Nx、Nθ、Nxθ、Nθx、Mx、Mθ、Mxθ、Mθx均为内力分量.

超声速轴向流作用下的圆柱壳气动力计算采用带有曲率修正的活塞理论公式[15](也适用于圆柱形扁壳),考虑初挠度后可以写为[8]

(4)

式中:q=1/2ρ0U2,ρ0为来流密度;U为来流速度;Ma为马赫数.

将式(4)代入式(1)中,并引入无量纲量

(5)

得到无量纲气动弹性运动方程为

(6)

相应无量纲边界条件表示为

ε=0,ε=1时,v=w=w0=Nε=Mε=0,即

(7a)

φ=0,φ=1时,u=w=w0=Nφ=Mφ=0,即

(7b)

2　二维DQM离散系统运动方程

依据微分求积法(以下简称DQM)二维问题的离散化方法[16],在0≤ε≤1,0≤φ≤1的区域内,分别在ε和φ方向上置入N和M个网格点,于是在平行于ε的任一直线φ=φj上,j=1,2,…,M,函数η(ε,φ)在网格点(εi,φi)处,对ε的1～4阶偏导可近似写为

(8)

同样地,在任一圆弧ε=εi上,i=1,2,…,N,函数η(ε,φ)在网格点(εi,φj)处,对φ的1～4阶偏导可近似写为

(9)

同理,对应力函数μ和初始挠度η0的各阶偏导也可以写做类似形式.其中,权系数A和B的确定参见文献[16],在此网格点形式中取文献[16]的非均匀网格点.

根据式(8)、(9),可以将无量纲形式的圆柱形扁壳气动弹性方程式(6)写为DQM离散后的形式，即

(10 a)

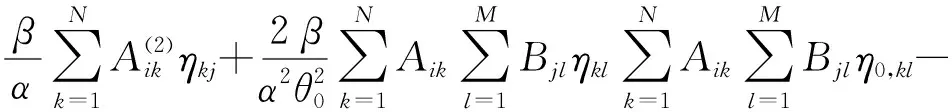
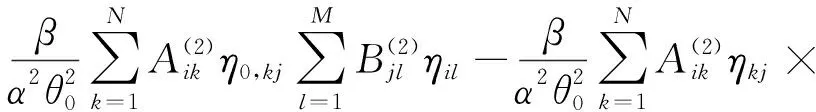
(10b)

边界条件式(7)的DQM形式为

ε=0,1时，

(11a)

φ=0,1时，

(11b)

写成DQM的简洁矩阵形式为

(12a)

(12b)

式中：

η0为不含边界变量的无量纲初始挠度矩阵;

η为不含边界变量的无量纲位移矩阵，

μ为不含边界变量的无量纲Airy应力函数矩阵,

(13)

具有一般矩阵形式的气动弹性方程可以写成

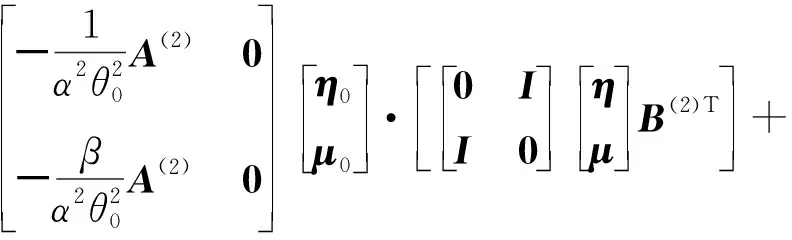
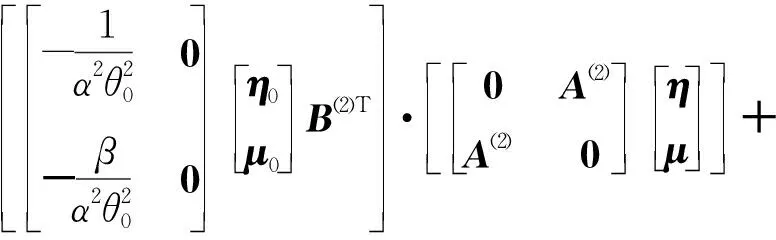
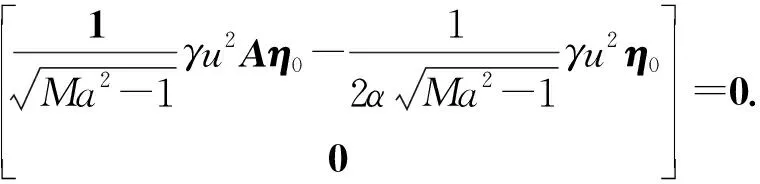
(14)

式(14)中,因不考虑初始挠度引起的应力,显然含有μ0的系数项皆为0.引入边界条件式(11),将含有初始挠度的矩阵η0先行代入,求得相应的系数阵,连同代入边界条件后含有所有位移矩阵和应力矩阵的方程(在此不再列出)一起进行“Kronecker”矩阵转换.经过“Kronecker”转换,原矩阵形式的变量矩阵可以展开为一维的列向量.同时,将带有初始挠度的系数阵也展开为一维列阵,然后将其转化为对角阵,变点乘为叉乘,这样,对于“Kronecker”转换后的一维列向量,重新构造得到新的系数阵,新的系数阵可以写为

(15)

式中：I为单位阵;

M为质量阵;

C为阻尼阵;

Rd为不含边界变量的右刚度系数阵;

Ld为不含边界变量的左刚度系数阵;

Rb为边界变量的右刚度系数阵;

Lb为边界变量的左刚度系数阵;

F0为转换后的初始挠度系数阵.

式(14)的简写形式为

(16)

3　系统颤振临界动压分析

一般情况下,圆柱形扁壳的初始挠度可以通过事先精确测量获得,形成离散的测量数据,直接代入式(14)～(16)中进行变换求解得到初始挠度系数矩阵,然后进行方程求解.根据圆柱形扁壳的几何特征和受力特性,在此,考虑几种特殊情况下的初始挠度,研究在这些初始挠度情况下,圆柱形扁壳线性系统的颤振临界动压.

假设圆柱形扁壳的初始挠度形式为[12-13]

(17)

代入无量纲量

ε=x/L,η0=w0/L,φ=θ/θ0,

k0=κA0/L,κ=L/h,

则式(17)为

(18)

令k0为初始挠度缺陷因子,n0、m0分别为周向半波数和轴向半波数.在给定k0、n0、m0的条件下,η0为ε、φ的确定函数,因此可以通过公式求导得到系数矩阵.一般的情况下,η0为离散的数据,可利用式(8)、(9)进行数值求导得到系数矩阵.

3.1　初始挠度缺陷因子对颤振临界动压的影响

曲率是影响圆柱形扁壳颤振临界动压的一个重要因素.抛开曲率因素,单纯地研究初始挠度缺陷因子的影响是片面的.在此,首先选取一个较小的曲率参数,来研究初始挠度缺陷因素k0、n0、m0对颤振临界动压的影响情况,然后,再与其它曲率参数的结果进行比较.取计算参数为[17]

(19)

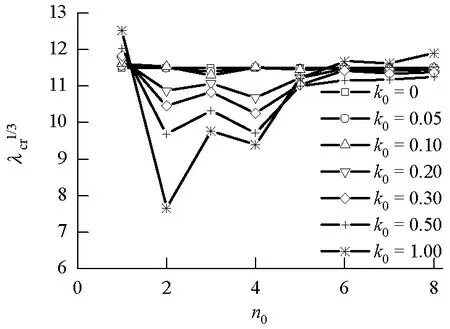
(a) m0=1

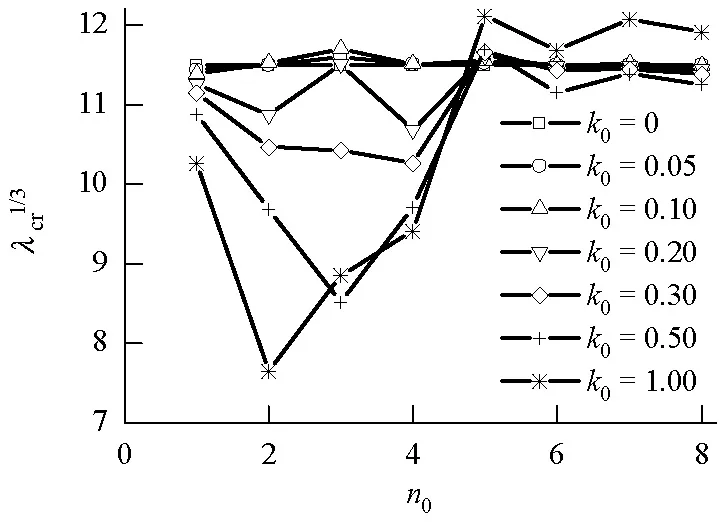
(b) m0=-1图1　小曲率α=20、θ0=0.05时,初始挠度缺陷因子对颤振临界动压的影响Fig.1　Effect of initial deflection imperfection factor on the flutter critical aerodynamic parameter at small curvature wherein α=20, θ0=0.05

半波数n0的变化.

由图1(a)可知,当m0=1、n0=1时,随着初始

挠度因子k0的增加,颤振临界动压呈现增大的趋势,这种趋势在m0=-1、n0=1时相反,说明当m0=1、n0=1时,k0的增加实际上使得扁壳曲率的增大,曲率的增大带来了颤振临界动压的提高,而m0=-1、n0=1时,反之，图2为两者的对比情况.

由图2可见,在这种特定参数下,颤振临界动压参数的变化与初始挠度缺陷因子成比例关系.当m0=1、n0>1时,k0的变化对颤振临界动压的影响变得复杂起来.n0=2、n0=4时,随着k0的增加,颤振临界动压显著下降,下降幅度高于n0=3时.当m0=1、n0>4时,k0增加,颤振临界动压变化不显著.当m0=-1、n0>1时,n0=2、n0=4时,k0对颤振临界动压的影响与m0=1时相同,n0=3时,k0对颤振临界动压的影响也非常显著.当m0=-1、n0>4时,k0增加,颤振临界动压变化不显著.

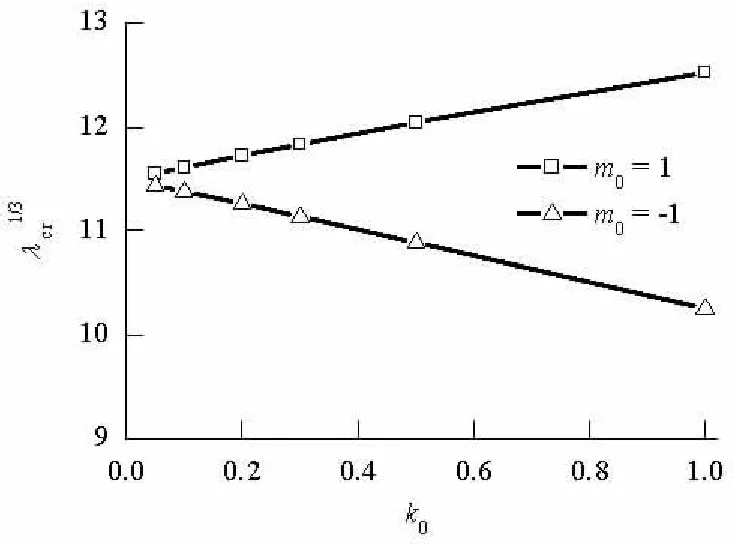
图2　n0=1时,颤振临界动压参数随初始缺陷因子的变化Fig.2　Flutter critical aerodynamic parameter vs initial deflection imperfection factor at n0=1

图3给出3种不同情况下无量纲频率Ω特征值虚部随无量纲动压λ变化曲线.

(a) k0=0(b) n0=2, m0=-1, k0=0.1(c) n0=2, m0=-1, k0=0.5图3 n0=2时,无量纲特征值虚部随动压变化Fig.3 Imaginary parts of non-dimensional eigenvalues vs aerodynamic pressure at n0=2

由图3可见,随着初始挠度缺陷系数的增加,系统产生颤振的频率阶数发生了变化,由先前的1～2阶模态耦合颤振,变成了2～3阶模态耦合颤振.这是由于随着初始挠度因子的增大,耦合颤振的周向半波数发生了变化,并由此导致了颤振临界动压的显著变化.对于不同的n0,这种变化具有差异性.这说明初始挠度的形式会影响产生颤振的周向半波数.

3.2　不同曲率时初始挠度周向半波数对颤振临界动压的影响

对于不同曲率的圆柱形扁壳,初始挠度缺陷对颤振临界动压的影响是不同的,这尤其表现在不同的初始周向半波数n0上.图4给出了α=5,θ0=0.2 圆柱形扁壳的研究结果，其它计算参数同式(19).

由图4可见,当n0=1时,增加初始挠度缺陷因子并没有改变系统颤振临界动压,这是因为此处所取的曲率参数较大,初始挠度因子的增加并不能显著改变扁壳的曲率,而影响系统颤振临界动压.当n0>1时,随着初始缺陷因子的增大,系统颤振临界动压显著减小,并且当n0>3时,这种影响依然明显,与小曲率情况不同.这是由于随着初始挠度因子的增大,产生耦合颤振的周向半波数比小曲率扁壳大,导致了较高的初始挠度周向半波数也会显著影响颤振临界动压.

(a) m0=1(b) m0=-1图4 大曲率α=5、θ0=0.2时,初始挠度缺陷因子对颤振临界动压的影响Fig.4 Effect of initial deflection imperfection factor on the critical flutter aerodynamic parameter at large curvature wherein α=5, θ0=0.2

4　结　论

(1) 当圆柱形扁壳的曲率较小时,单一的沿外法线方向的初始挠度会显著提高系统的颤振临界动压,而单一的沿内法线方向的初始挠度则会降低系统的颤振临界动压,这种影响与初始挠度因子成线性关系.而对于曲率较大的圆柱形扁壳,这种单一的初始挠度类型对系统颤振临界动压的影响并不显著.

(2) 当初始挠度包含的周向半波数大于1时,不同曲率的圆柱形扁壳颤振临界动压受初始挠度缺陷因子的影响不同.当曲率较小时,周向半波数n0=2，3，4时,随着k0的增加,颤振临界动压显著下降,n0>4时,参数k0的增加带来的颤振临界动压变化并不显著.当曲率较大时,随着初始缺陷因子的增大,系统颤振临界动压显著减少,并且当n0>4时,这种影响依然明显.

(3) 对于特定的初始挠度缺陷类型,随着初始挠度缺陷系数的增加,其含有的某些周向半波数会使系统产生耦合颤振的频率阶数发生变化,并由此导致了颤振临界动压的显著变化.这说明初始挠度的形式会影响产生颤振的周向半波数.这对飞行器颤振设计而言是不利的.