基于经验模态分解的轨道不平顺时频特征分析

杨友涛,　刘国祥

(1. 西南交通大学地球科学与环境工程学院, 四川 成都 611756; 2. 西南交通大学高速铁路运营安全空间信息技术国家地方联合工程实验室, 四川 成都 611756; 3. 西南交通大学土木工程学院, 四川 成都 610031)

轨道不平顺是指轨道的实际位置、几何尺寸相对设计位置和设计尺寸的偏差,是由很多随机因素共同作用的结果.主要包括线路施工过程中的偏差、钢轨的初始平直性、道床、路基等构筑物的不均匀沉降及残余变形积累,以及机车车辆等荷载的不规则变化的动力作用[1]等因素.由于这些不确定性因素的共同作用,使得轨道不平顺具有随机性,主要采用均值、方差等统计数据表示其特性.目前,我国轨道几何状态评价主要采用局部幅值超限方法和轨道质量指数方法,这两种方法从空间域(线路里程)幅值方面进行评价,具有一定的局限性.

有学者利用信号的时频分析方法对轨道动态不平顺数据进行分析,文献[2-3]中利用小波分析理论对轨道不平顺局部高频灾害进行检测，提取不同波长范围的轨道不平顺.文献[4-5]中利用小波和Wigner-Ville相结合的方法对轨道不平顺特征进行提取与分析.文献[6]中利用短时傅里叶变换、魏格纳变换和Gabor变换等时频分析方法分析了轨道实测振动加速度信号,提取了长波不平顺信号.短时傅立叶变换采用固定时间窗口的函数进行计算,不能根据信号的特点来调整时间分辨率和频率分辨率,没有自适应能力.小波变换克服了短时傅立叶变换时间窗口大小不随频率变化的缺点,可根据信号频率的高低自适应调整时频窗口的大小,但仍受Heisenberg不确定原理限制,不能精确表示频率随时间的变化.另外,各个小波基函数的适用范围不一样,选择适合待分析信号的小波基函数是小波分析的难点,使小波分析不具有自适应性.

与以上建立在先验基函数上的时频分析方法不同,经验模态分解(empirical mode decomposition, EMD)是以信号本身的时间尺度特征为基础的自适应分解方法,更适合非线性、非平稳信号分析.经验模态分解与希尔伯特变换相结合,更能揭示隐藏于信号中的内在物理信息[7].针对经验模态分解仅能处理一元数据的不足, Rehman提出适合于多通道信号分析的多元经验模态分解(multivariate empirical mode decomposition, MEMD)[8].多元经验模态分解把多元数据分解为具有相同数目的本征模态函数,可以减少各层模态混叠和尺度不对齐的问题,具有自适应性[9].本文利用多元经验模态分解(intrinsic mode functions, IMF)和希尔伯特变换方法,对轨道几何不平顺的时频特征分布进行分析,为线路养护维修、列车安全运行提供技术支持.

1　希尔伯特-黄变换方法

1.1　多元经验模态分解

经验模态分解是以数据驱动方式把非线性、非平稳信号分解为多个幅值-频率调制的本征模态函数以及残余分量[7],其表达式为

(1)

式中:x(t)为信号;cm(t)为IMF;m为IMF层数;r(t)为剩余分量;t为时间.

本征模态函数包含不同的频率成份,反映了信号的不同波动情况.每个本征模态函数必须满足条件[7]:(1) 在整个数据范围内,极值点和过0点的个数相等或相差1个;(2) 由极大值和极小值计算的包络值之和为0.

经验模态分解通过循环筛分的方法把满足上述两个条件的IMF分解出来.在一元经验模态分解中,通过对信号的极大值和极小值分别内插计算获取上、下包络线,然后对其取平均得到局部均值[7],对于多元数据,不能直接定义极值.

为解决这个问题,多元经验模态分解把多元信号X(t)=(x1(t),x2(t),…,xn(t))沿不同方向投影到n维空间上,计算这些投影序列的极值并进行内插,得到投影序列的包络线,这些包络线的平均值即为多元信号的局部均值[8].多元经验模态分解的计算过程如下:

(1) 在n-1维超球面上选择合适的均匀采样点集θk,获得n维空间的方向向量集vθk,k为方向向量个数,k=1,…K;

(2) 计算多元信号X(t)在每个方向向量vθk上的投影向量Pθk(t);

(3) 找出所有投影向量集中,每个投影向量极大值所对应的时刻ti,θk,i为极大值点的序号;

(4) 利用样条函数对极值点(ti,θk,X(ti,θk))进行插值,获得K条包络曲线eθk(t);

(5) 计算K个方向向量的包络线均值

(2)

(6) 提取高频细节信号d(t),d(t)=X(t)-m(t).如果d(t)满足多元IMF的停止准则,记C1(t)=d(t)为第 1层多元IMF,将X(t)-d(t)作为(2)中输入信号,继续提取多元IMF;否则,将d(t)作为输入信号继续迭代计算.

经过多元经验模态分解后,多元信号分解为不同尺度的多元IMF和多元剩余分量之和的形式为

(3)

式中Cm(t)=(c1，m(t),c2，m(t),…,cn，m(t))为n元IMF;R(t)=(r1(t),r2(t),…,rn(t))为n元剩余分量.

1.2　希尔伯特谱分析

通常,瞬时频率和瞬时幅值用于表征非平稳、非线性信号的短暂特性.但是,对于多分量组成的非平稳信号,瞬时频率没有明显的物理意义.所以,首先利用经验模态分解将多分量信号分解为一系列单分量的IMF,然后利用希尔伯特变换计算其瞬时频率和瞬时幅值.对于单一成分的本征模态函数cj,m(t),其希尔伯特变换为

(4)

式中:P为柯西主值；j为多元变量序号.

相应的解析信号形式为

Zj，m(t)=cj,m(t)+iH(cj,m(t))=aj,m(t)eiφj,m(t).

(5)

信号瞬时幅值aj,m(t)和瞬时相位φj,m(t)的计算式为

(6)

通过对瞬时相位求导,可得瞬时频率为

(7)

通过希尔伯特变换计算瞬时频率,有时会出现较大的波动,甚至出现负频率的情况.同时,希尔伯特变换具有端点效应,即在信号两端的瞬时频率具有能量泄漏的问题[10].文献[10]中在希尔伯特变换求取瞬时频率的基础上,提出标准化希尔伯特变换,采用经验调频-调幅分解方法,减弱了IMF中的调幅分量,仅保留了调频分量,从而使瞬时频率的计算不再受Bedrosian等式的限制.文中轨道不平顺的瞬时频率采用标准化希尔伯特变换计算.

通过对每一个IMF进行希尔伯特变换,信号xj(t)表示为

(8).

用式(8)可在三维坐标图中,将瞬时幅值和瞬时频率表示为时间的函数,即在时间和频率联合平面内表示幅值的变化.这种幅值随时间和频率(f)变化的分布函数为信号的希尔伯特谱,其表达式为

(9)

2　轨道几何不平顺数据分析

轨道几何不平顺用轨距、水平、左高低、右高低、左轨向、右轨向和扭曲7个参数来描述,其表示为随里程变化的随机函数.

本文选取轨道检查车在沪宁城际上的轨道动态检查数据进行分析,检测速度为252 km/h,样本数据里程为上行K104+000.00～K104+999.75,轨检车数据采样间隔为0.25 m.

2.1　轨道不平顺多尺度分解

对预处理后的轨道不平顺信号进行多元经验模态分解,得到13层IMF(C1～C13)和1个趋势项,分解结果见图1、2.

由图1、2可以看出,随着IMF序号的增加,其空间变化尺度逐渐增大;7个轨道不平顺参数中,相同序号的IMF具有相近的空间变化尺度.根据多元经验模态分解这一特点,按信号内在规律分解出多元序列相近尺度的分量.轨距和右轨向不平顺的第2层和第3层IMF在里程K104+485.00前后有大的幅值异常值,见图示.在数据预处理阶段采用3倍中误差准则并没有探测出该里程位置的异常值,但是经过经验模态分解后有异常值出现.

2.2　轨道不平顺频率分析

对轨道不平顺分解的各层IMF进行标准化希尔伯特变换,计算各个IMF的瞬时频率和瞬时幅值.

为直观表示轨道不平顺各IMF瞬时频率的变化,计算其平均频率.计算平均频率有两种方法:

(1) 根据极值点或过0点个数计算平均频率[11-12];

(2) 利用信号的瞬时频率计算平均频率[13-14].

按极值点和过0点个数确定平均频率的方法,在高阶IMF中,由于极值点和过0点位置的不均匀性,平均频率的计算结果误差较大.

文献[14]中利用瞬时频率的算术平均值和能量加权均值表示平均频率,能量权重平均频率可写为

(10)

式中:L为时间长度.

根据瞬时频率所占的权比来计算平均频率的几种方法,更能直观的反映每层IMF的频率变化情况[13-14].本文采用瞬时频率能量权重的方法,即按式(10)计算轨道不平顺各IMF的平均频率及平均频率标准差.与式(10)相对应,平均频率标准差也考虑能量权重,则加权标准差计算式为

(11)

图1　轨道几何不平顺多元经验模态分解结果 (A)Fig.1　MEMD results of irregularities in track geometry (A)

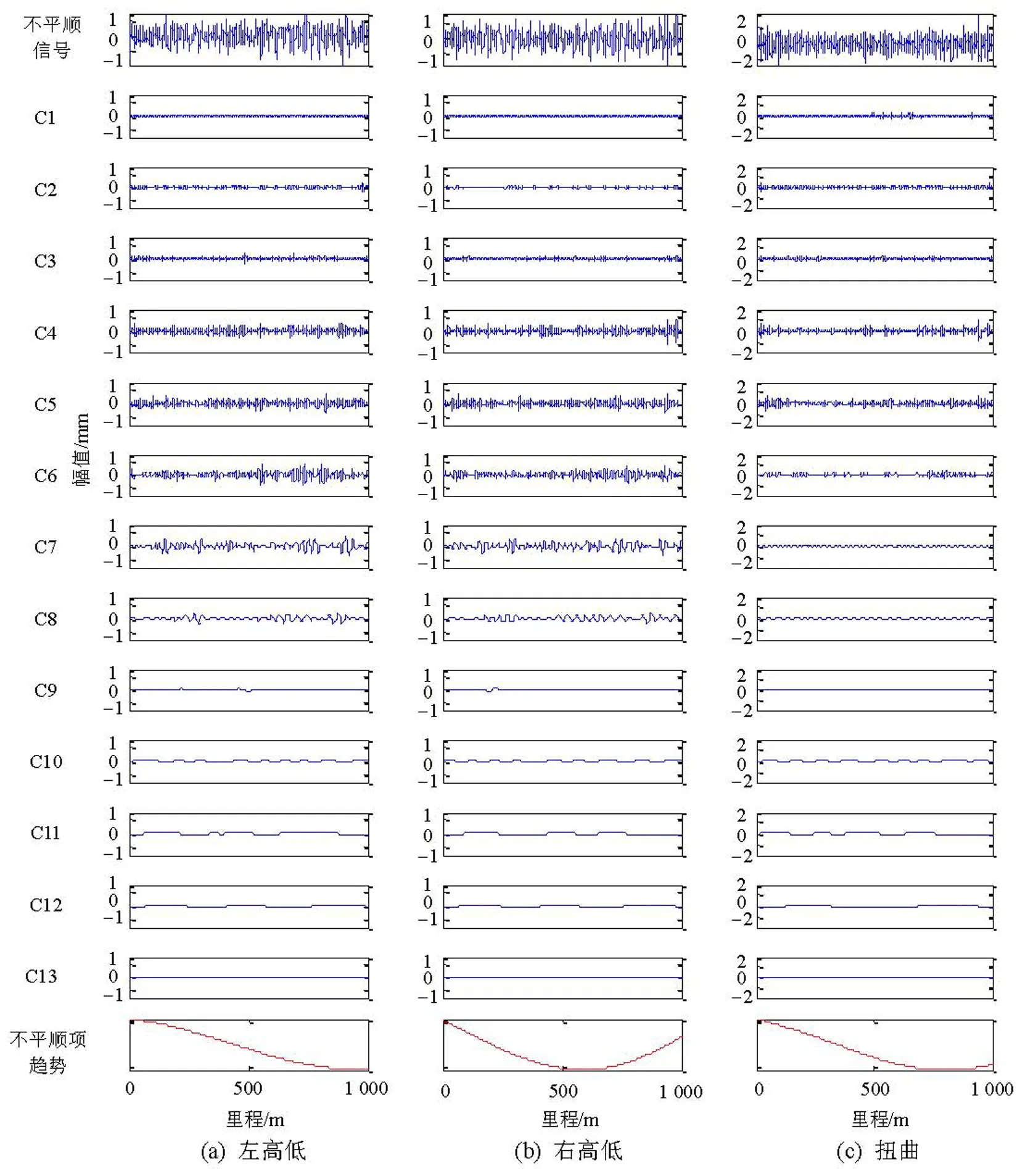
图2　轨道几何不平顺多元经验模态分解结果(B)Fig.2　MEMD results of irregularities in track geometry (B)

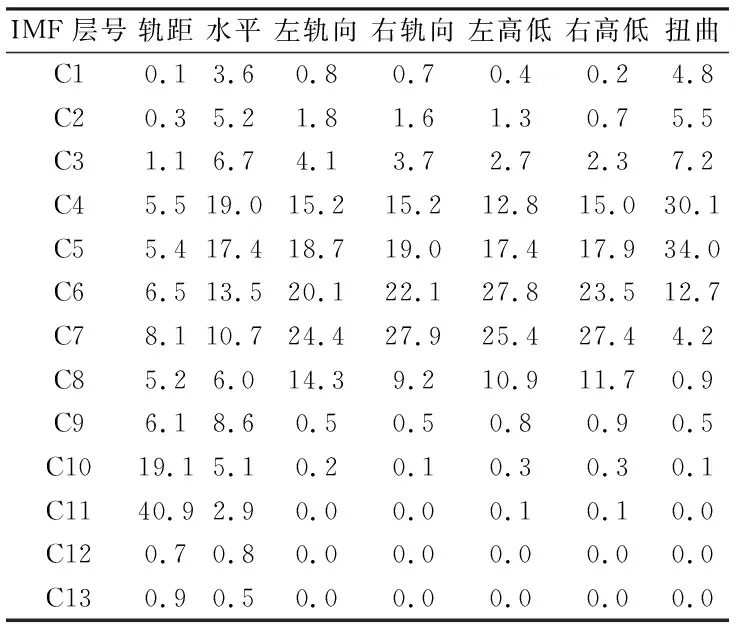
为减少希尔伯特变换边界效应对平均频率的影响,在轨道不平顺的每个IMF平均频率及标准差计算中剔除了样本数据两端的部分数据,其计算结果如表1所示.表中,相对标准差指每个IMF的平均频率的标准差与其平均频率的比值.

从表1可以看出:(1) 轨道不平顺7个参数中,经多元经验模态分解得出的同层IMF的平均频率基本一致,每层IMF中平均频率相对较差最大的为第13层的IMF,其原因是高阶IMF的平均频率计算误差较大造成的;其他各层的平均频率相对较差很小,说明经多元经验模态分解的轨道不平顺各层的IMF频率具有一致性[9].(2) 每个轨道不平顺参数的各层IMF的平均频率逐渐减少,并且其值约为上一层IMF平均频率的1/2.文献[9]中通过对白色噪声进行经验模态分解,得出该方法具有二进滤波特性,轨道不平顺数据的频率分布与白色噪声具有相似性,说明轨道不平顺数据具有随机特性.(3) 不同序列的同层IMF的平均频率相对标准差差别较小,其中：第1层IMF的相对标准差较大,其值为0.4左右,说明第1层瞬时频率波动较大,可能是信号中含有高频噪声所致;第2～13层IMF的相对标准差均较小,说明多元经验模态分解方法获得的轨道不平顺的频率带宽较窄,瞬时频率波动较小.

表1　轨道不平顺各层IMF的平均频率和相对标准差Tab.1　Average frequency and relative standard deviation of IMFs of track irregularity

多元经验模态分解方法是根据数据本身的波动情况自适应的分解为多层IMF.本文选取的轨道不平顺样本数据被分解为13层,其平均波长(空间频率的倒数)范围为0.7～761.4 m,说明轨道不平顺数据是由不同波长组成的多分量随机函数.

目前轨道检查车的最大检测波长为200 m,由多元经验模态分解方法得出的最大波长远超此范围,说明利用多元经验模态分解方法获得的IMF有虚假波长成份,所以如何根据轨道不平顺数据的实际波动情况选择有效的IMF也是需要解决的问题.

2.3　轨道不平顺能量分布

文献[14]中在分析小波尺度图的基础上,提出多元经验模态分解尺度图,即用各层IMF的瞬时幅值的平方来表示信号不同尺度的能量变化.根据式(8),信号的多元经验模态分解尺度图可表示为

(12)

多元经验模态分解尺度图在时间和尺度的联合平面内表示能量的变化情况,轨道不平顺7个参数的多元经验模态分解尺度图如图3所示.

由图3可以看出,轨距和水平不平顺的能量分布较为广泛,涵盖在第3～11层IMF范围内,轨距的第11层IMF能量所占比重较大,其能量主要分布在低频部分;轨向和高低4个不平顺参数的能量主要集中在中间频段的IMF中,低频和高频段范围的能量几乎可以忽略不计;扭曲不平顺的能量主要分布在前6个IMF中,即高频部分.

综上所述，通过多元经验模态分解尺度图也能确定轨道不平顺在不同尺度内沿里程方向上能量的突变,可为精确查找轨道病害,进行养护维修提供了基础.

表2为根据多元经验模态分解尺度图统计出的各层IMF能量所占的比例.由表2可以看出：

(1) 轨距不平顺中，第11层IMF所占能量达到40.9%,主要原因是在里程K104+500.00～K104+980.00范围内轨距不平顺幅值有大的波动.

(2) 轨向和高低能量分布比较集中,第4～8层 的IMF能量之和比例达到90%以上,从表1可知，第4～8层的IMF对应的空间平均波长为4.37、7.58、14.11、23.96、35.56 m,即能量主要分布在波长为4～36 m的范围;同时在每层IMF中左右轨向、左右高低的能量百分比比较一致,说明左右轨道的轨向、高低的能量分布具有相关性.

(3) 扭曲不平顺能量主要集中在高频部分,其中第4、5层IMF能量所占比例均大于30%；第8～13层IMF所占能量比例之和仅为1.5%,低频段能量的影响很小.

多元经验模态分解尺度图能清晰的标识轨道不平顺在不同尺度上的能量分布.轨道不平顺样本数据中,除轨距不平顺外,其他不平顺的能量主要分布在中波区段,且能量分布相对集中.通过以上分析,能更好的掌握轨道不平顺的能量和波长分布规律,可以有针对性的对轨道进行养护维修,提高铁路运行的安全性.

图3　轨道不平顺多元经验模态分解尺度图Fig.3　MEMD-based scalograms of track irregularity

IMF层号轨距水平左轨向右轨向左高低右高低扭曲C10.1 3.60.80.70.40.24.8C20.35.21.81.61.30.75.5C31.16.74.13.72.72.37.2C45.519.015.215.212.815.030.1C55.417.418.719.017.417.934.0C66.513.520.122.127.823.512.7C78.110.724.427.925.427.44.2C85.26.014.39.210.911.70.9C96.18.60.50.50.80.90.5C1019.15.10.20.10.30.30.1C1140.92.90.00.00.10.10.0C120.70.80.00.00.00.00.0C130.90.50.00.00.00.00.0

3　结　论

基于多元经验模态分解方法和希尔伯特变换,对高速铁路轨道动态不平顺进行时频特征分析和应用研究,得出以下主要结论:

(1) 多元经验模态分解方法用于分析多元数据序列,减少了标准经验模态分解方法中的模态混叠和多元序列尺度不对齐的问题,具有很好的自适应性和时频局部化能力.希尔伯特变换计算多元序列的瞬时频率和瞬时幅值,能反映多元数据序列的局部时频分布特征.

(2) 用多元经验模态分解方法,分解出的轨道几何不平顺各层IMF的频率带宽较窄,轨道不平顺在不同尺度下的频率波动较小;轨道不平顺不同参数的同层IMF的平均频率相差较少,具有一致性.

(3) 多元经验模态分解尺度图能直观的反映轨道不平顺的能量分布,样本数据的轨距不平顺能量主要分布于中长波区段,波长频段范围较广;轨向和高低能量分布相对集中,主要集中于空间波长4～36 m范围;扭曲的能量主要集中分布在波长为4.9、7.6 m的两个尺度内.

为更好的提取轨道不平顺的时频特征,应对整条线路轨道不平顺数据按线路类型、轨道结构以及线下结构等分门别类的进行特征分析,同时比较轨道不平顺数据在不同检测时间的时频变化特征.