基于阶段演化特征的稠油氧化动力学

袁士宝, 赵黎明, 蒋海岩, 程海清

(1.西安石油大学石油工程学院,陕西西安 710065; 2.陕西省油气田特种增产技术重点实验室,陕西西安 710065;3.中国石油辽河油田分公司,辽宁盘锦 124010)

近年来,注空气提高采收率技术得到了国内外学者的广泛关注[1-2]。注空气驱油的反应机制得到了进一步的明晰[3-4],矿场试验成功的关键因素也得到普遍认可[5-8]。原油氧化动力学的研究是注空气提高采收率技术的基础理论[9],学者们在反应动力学参数计算[10-13]和反应阶段[14-17]方面进行了许多探索。但是在利用热重实验分析原油氧化动力学规律时注重反应活化能的求取,而简单地将原油氧化反应级数n设定为0或1[18-19],忽视了反应级数对反应机制方程选取的影响,进而影响动力学参数的确定。笔者基于稠油热重分析(thermal gravity analysis,TGA)实验,首先通过Coats-Redfern积分法对不同氧化反应阶段的反应机制函数差异性进行分析,对各氧化反应阶段的反应机制函数进行计算,深入分析各反应阶段内在机制及动力学参数计算所应注意的问题。

1　原油氧化热重实验

实验采用的油样来自辽河油田,地面脱气原油黏度为1 362.5 mPa·s,常温下油样的密度为0.946 4 g/cm3,胶质沥青质含量为30%～40%,属于典型的普通稠油。

采用德国耐驰热重分析仪进行实验,在不同升温速率3、5和7 ℃/min下进行热重(thermal gravity, TG)分析。进而对原始数据进行等间距抽稀。得到TG曲线和失重速率(derivative thermogravimetric analysis,DTG,即差热重量分析，DTG是TG的二次微分曲线)曲线如图1所示。

图1　不同升温速率下油砂热失重结果对比Fig.1　Comparison of thermal weight loss results of oil sand at different heating rates

在前期研究基础上,通过TGA实验的失重速率分析可知,该原油体系氧化反应可以分为4个连续阶段,这4个阶段主要包括低温(小于180 ℃)氧化反应前段、低温(180～350 ℃)氧化反应后段、燃料沉积段(350～440 ℃)、高温(大于440 ℃)氧化反应阶段[16],其中燃料沉积阶段既不是高温氧化反应主导也不是低温氧化反应主导,独立划分为一段。

2　氧化动力学计算方法的选取

目前基于TG实验的氧化动力学参数计算主要有积分法和微分法两种,积分法可以平滑掉实验数据产生的波动性,微分法便于研究实验过程的细节变化规律。微分法在采用插值或拟合方法求反应速率的过程中,由于插值或拟合函数与动力学模型之间的差异,会引入明显的误差,计算结果随机性很大,结果往往不可靠,需要作图和大量数据处理,数据处理费时,而且误差较大[20-21]。

由于实验环境本身的影响因素不确定,会造成实验数据的波动,采用微分法误差较大,选择Coats-Redfern积分法对氧化动力学参数进行计算,以便于平滑实验数据产生的波动性,提高曲线拟合的可靠性。Coats-Redfern积分法的主要公式为

(1)

式中,G(a)为积分机制函数;f(a)为微分机制函数;T为温度,K;E为活化能,kJ/mol;R为气体常数,8.314 J/(mol·K);A为指前因子,min-1;β为升温速率,℃/min。

设反应机制函数为f(α)=(1-α)n得到常用的Coats-Redfern方程[22]为

(2)

其中

α=(w0-wt)/(w0-wf).

式中,α为原料剩余量;w0为初始燃料质量,mg;wt为原料在某时刻质量,mg;wf为反应终了剩余固体质量,mg;n为反应级数(有著作称为经验机制函数幂指数)。

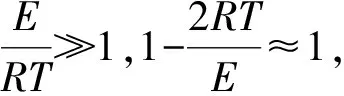
在通过Coats-Redfern方程计算氧化反应动力学参数后,需要对计算的正确性进行检验,本文中采用可在未知反应级数的情况下计算活化能的Flynn-Wall-Ozawa(FWO)方法进行检验,当Coats-Redfern方法计算得到的活化能E与FWO方法计算得到的活化能E接近时,认为结果可靠,

(3)

3　计算结果分析

3.1　氧化反应阶段差异性分析

利用Coats-Redfern方程计算反应动力学参数,选取简单反应机制方程f(α)=(1-α)n,并假设该简单反应机制方程形式适用于各个氧化反应阶段,首先假设反应级数n=0,将原油TG实验数据代入式(2)计算;绘制Coats-Redfern曲线,得到Coats-Redfern曲线,分别取n为1和0.5,重复以上步骤;通过各个反应阶段曲线的线性度选取不同的反应级数。

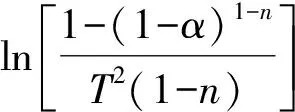
图2　升温速率3 ℃/min时Coats-Redfern曲线Fig.2　Coats-Redfern curve at heating rate of 3 ℃/min

由图2可知,不同级数n下的Coats-Redfern曲线在低温氧化前段没有表现出明显的差异,不符合氧化反应的动力学规律,分析认为该阶段主要以挥发、相变等作用为主,氧化反应并不是主导反应。从低温氧化反应后段开始,氧化反应开始逐渐增强,表现为不同反应级数的Coats-Redfern曲线逐渐分离,出现差异;当n=0.5时低温反应后段的线性度最好。由于低温氧化反应前段差异性较小,所以建议在整个低温氧化反应阶段选取反应级数n=0.5进行动力学参数计算。

在高温氧化阶段, Coats-Redfern曲线在高温氧化反应后段不稳定,该方法不合适于温度大于560 ℃时的动力学参数分析。在高温反应段,反应级数n=1时曲线线性度为0.96～0.98,活化能为50～60 kJ/mol。不同升温速率下不同反应级数计算得到的线性度如表1所示。

表1　不同氧化反应阶段反应级数计算结果

在不同氧化反应阶段,机制函数f(α)=(1-α)n反应级数不同,说明不同氧化反应阶段的反应机制的差异性,而简单反应机制函数是否能适用于所有氧化阶段的动力学参数计算就成为首要问题,须结合阶段反应物理化学过程深入探究其反应机制函数。

3.2　基于反应机制函数的氧化内在机制

3.2.1低温氧化反应前段动力学参数

通过分析可知Coats-Redfern方法在燃料沉积段计算原油氧化动力学参数并不适用,所以仅作低温氧化及高温氧化段的计算分析。利用文献[22]中给出的30组反应机制函数进行计算原油氧化动力学参数。将不同的反应机制函数代入式(1),通过低温氧化反应前段的Coats-Redfern曲线线性度选择确定该反应机制函数下的活化能E和置前因子A,结果见表2。表2中已经删除线性拟合度差、计算结果不合理的机制方程,函数编号与原文献一致。

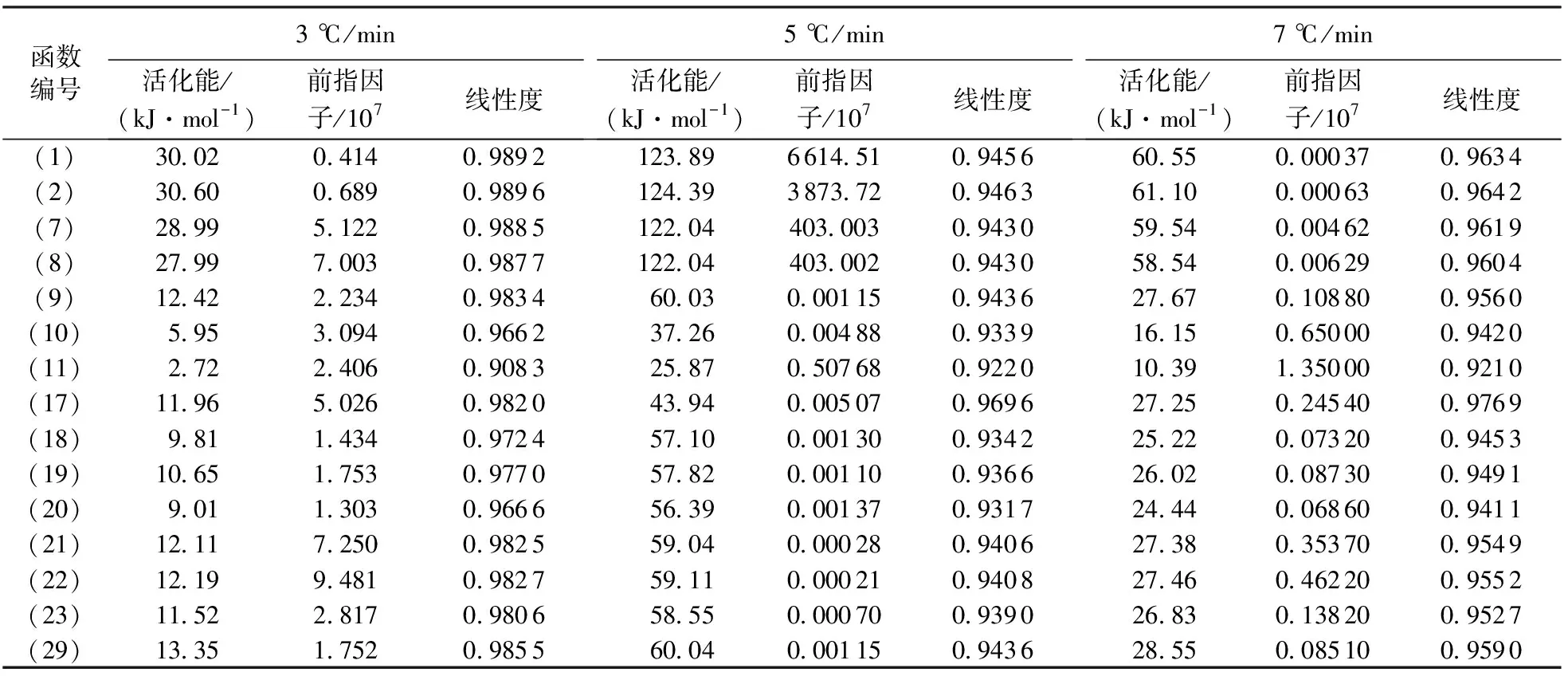
表2　低温氧化反应前段不同升温速率下各个机制函数计算结果

图3　低温氧化反映前段反应机制函数(17)在不同升温速率下计算得到曲线Fig.3　Curves calculated by reaction mechanism function (17) in different heating rate, front section of low temperature oxidation reaction

原油低温氧化反应前段主要以原油中水分及轻质组分的挥发和加氧反应为主,此时氧化断键反应并不是主导反应,仅有少量长链碳氢生成。该反应阶段中原油和水附着于砂粒表面,主要以相边界反应为主,与机制函数描述的相边界反应特征一致。反应生成的一些长链化合物可能增加了该阶段原油的氧化反应难度,导致在低温氧化反应前段活化能较大。

3.2.2低温氧化反应后段动力学参数

对低温氧化后段进行机制函数选取,函数(17)的线性拟合度最好,如图4所示。利用函数(17)作为反应机制函数,计算得到升温速率3、5和7 ℃/min下的活化能分别为13.74、16.93和14.44 kJ/mol,指前因子分别为4.05×107、3.14×107和4.58×107min-1。

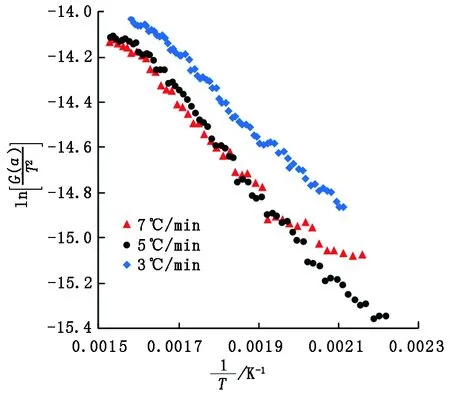
图4　低温氧化反应后段反应机制函数(17)在不同升温速率下计算得到曲线Fig.4　Curves calculated by reaction mechanism function (17) in different heating rate, post section of low temperature oxidation reaction

在低温反应后段的反应机制函数形式与低温氧化前段一致,描述了相边界反应。低温反应后段原油中的水分和轻质组分已经挥发完,该阶段原油氧化反应开始增强氧气与低温反应前段生成的部分长链液态碳氢化合物反应生成了一些短链化合物,并且有大量的中间产物,如醛、酮、醇等,是一个气液相边界反应。低温氧化反应后段活化能变低,氧化反应容易进行,而且随着温度的逐渐升高,反应速率明显加快。

3.2.3高温氧化反应段动力学参数

对高温氧化反应段实验数据计算并确定机制函数,计算得到函数(3)的线性拟合度最好,结果如图5所示。利用函数(3)作为反应机制函数,计算得到升温速率为3、5和7 ℃/min下的活化能分别为63.99、61.69和52.08 kJ/mol,指前因子分别为4.01×105、7.35×105和3.01×106min-1。

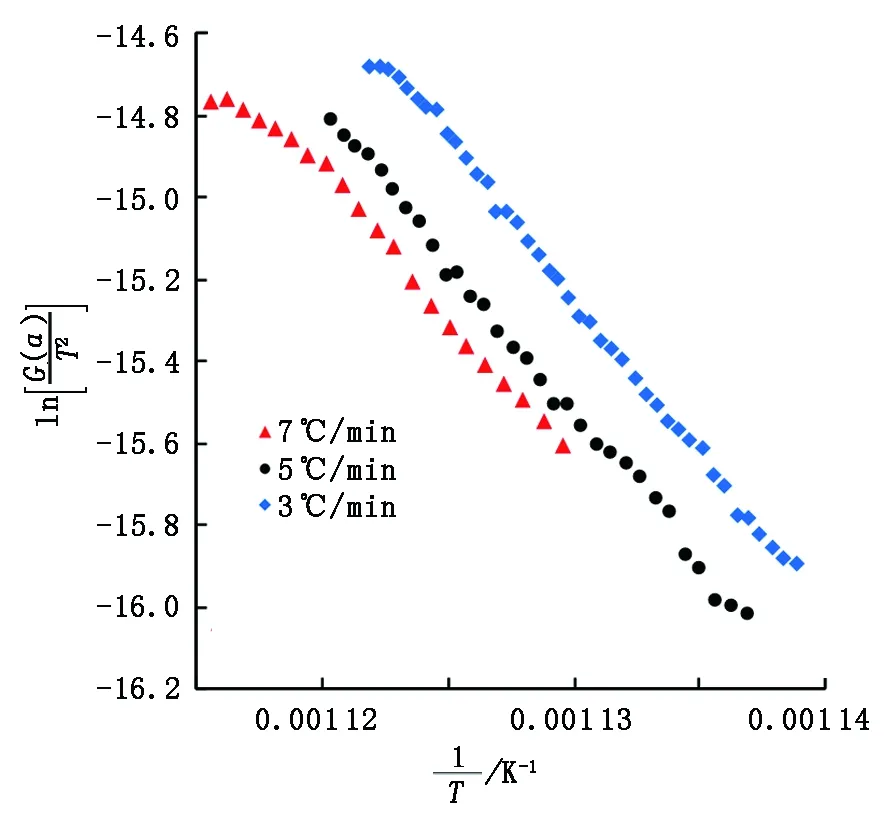
图5　高温氧化反应阶段反应机制函数(3)在不同升温速率下计算得到曲线Fig.5　Curves calculated by reaction mechanism function (3) in different heating rate， high temperature oxidation reaction stage

在原油高温反应阶段,燃料沉积阶段沉积的焦炭随温度的升高开始发生燃烧。该阶段反应主要发生在氧气和固体焦炭之间,反应活化能较大,生成CO2、H2O等产物,同时释放出大量的热。根据反应机制函数形式所揭示的机制,在高温反应阶段,随着相边界反应基本消失,氧气与焦炭开始充分接触并发生以三维扩散为主的反应,使该部位燃烧处于扩散控制工况。影响三维扩散反应的主要因素是空间的氧气浓度梯度,由其产生的物质传递过程为三维矢量过程。

3.3　计算合理性检验

Flynn-Wall-Ozawa方法避开了反应机制函数的选择而直接求出活化能E值,可以避免因反应机制函数的假设不同而可能带来的误差,因此常被用来检验活化能值[22]。为了检验分析结果的可靠性,利用Flynn-Wall-Ozawa方法计算活化能E与Coats-Redfern方法所得结果进行比较,检验其计算结果的正确性,结果见表3。

由表3分析可知,在低温反应前段受样品吸收水蒸气和轻组分蒸发的影响，两种方法计算得到的活化能存在很大差距，但在低温反应后段和高温反应阶段计算结果基本一致，说明通过Coats-Redfern方法选取的机制函数是准确的,计算所得的动力学参数可靠。

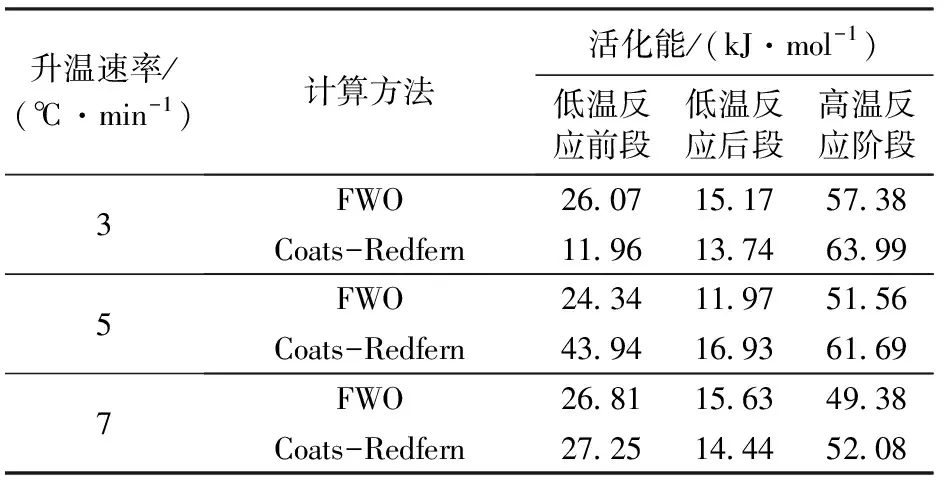
表3　活化能计算结果检验Table 3　Test results of calculation activation energy

3.4　原油黏度对反应机制函数选取的影响

为验证不同黏度对反应机制函数的影响,对S625(50 ℃黏度53.65 mPa·s)、G3(50 ℃黏度7 250 mPa·s)、SG-38-32(50 ℃黏度38 670 mPa·s)区块3种不同原油黏度进行热重分析实验,结果如图6所示。

图6　不同黏度原油热失重结果对比Fig.6　Comparison of thermal weight loss results of crude oil with different viscosity

由图6分析可得S625、SG-38-32、G3各区块原油样品,原油氧化阶段分段如表4所示。

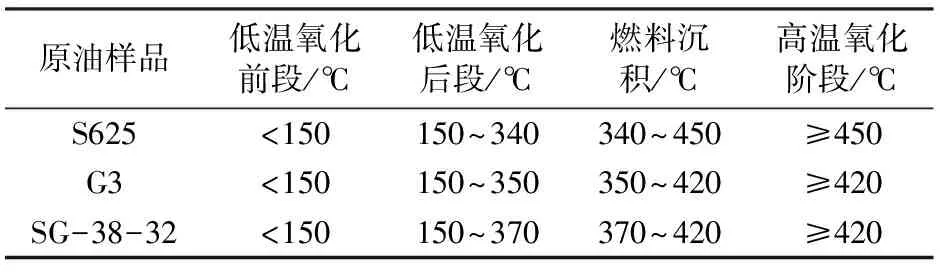
表4　不同黏度原油各氧化阶段的温度Table 4　Temperature range of oxidation stages of different viscosity crude oil

由表4分析可得,随着原油黏度的增加,原油低温氧化反应后期的温度范围越来越大,燃料沉积阶段的温度范围越来越小,这主要是因为低黏原油所含的轻质组分较多,重质组分较少,反应活性较高,而高黏原油所含重质组分较多,反应活性低,所以相对于低黏油,高黏原油的低温氧化反应阶段较长。

利用Coats-Redfern方程计算原油反应动力学参数,对文献[22]中提出的30种氧化机制函数进行拟合,选取不同黏度反应动力学方程，结果如表5所示。

计算结果显示S625区块的轻质油,在低温(小于150 ℃)氧化前期阶段,表现为全段的加氧反应过程,质量为增加状态,没有出现导致质量减少的氧化反应,拟合得没有适合该阶段的氧化机制函数。G3和SG-38-32区块原油黏度相对于S625区块较大,低温氧化阶段拟合较好,但是由于原油性质不同,在低温氧化反应前期所选取的氧化反应机制函数不同,在高温氧化反应阶段,由于燃料沉积阶段的产物均为焦炭,不论轻质油还是重质油在该阶段的反应均以焦炭燃烧为主,所以该阶段反应机制函数一致。

表5　不同黏度原油反应机制方程选择

4　结　论

(1)基于TG热重实验的Coats-Redfern方法适用于计算稠油氧化反应动力学参数。燃料沉积段不属于氧化行为,应用其他手段分析;普通稠油的氧化表现为低温氧化反应级数为0.5,反应活化能12～44kJ/mol。高温氧化反应级数为1,活化能为53～64kJ/mol。不同油品性质可能会出现偏差。

(2)低温氧化反应阶段以气液相界面反应为主,随着焦炭的不断生成并沉积在砂粒表面,到了高温氧化反应阶段就转化为氧气与焦炭的三维扩散反应,正是由于产物和其性质在不断变化,最终导致各阶段反应机制不同,描述其过程的反应机制函数也需要做相应调整,从而避免在动力学参数计算时出现较大误差。

(3)在原油氧化反应过程中,在不同反应阶段所发生的反应各不相同,不能采用简化手段将所有反应阶段反应级数笼统选取为0或1。应该应用不同的反应机制函数选取线性度最高的函数形式计算反应动力学参数,并应用FWO方法验证其计算合理性,进而认识氧化内在机制,指导注空气提高采收率技术。在原油低温氧化前段反应级数对氧化动力学参数的影响很小,从低温氧化后段开始影响逐渐显著,主要表现为除低温氧化前段的其他氧化阶段随着反应级数的升高Coats-Redfern曲线出现平移。