基于B-L方程的低渗透油藏CO2水气交替注入能力

孟凡坤, 苏玉亮, 郝永卯, 李亚军, 童　刚

(1.中国石油勘探开发研究院,北京 100083; 2.中国石油大学(华东)石油工程学院,山东青岛 266580;3.中国石油长庆油田分公司第一采油厂，陕西西安 710200)

低渗透油藏由于存在“三低”特性,在油藏后续开发过程中,地层能量补充及提高采收率较为困难[1-2]。国内外大量矿场实践及室内试验研究表明,相比于其他气体,CO2有较好的驱油特性,可大幅提高低渗透油藏采收率[3-4],但常规的连续注气(CO2)存在注入CO2突破过早、波及效率低的问题,CO2水气交替驱综合了水驱、CO2驱的优点,不但可提高波及系数,还可增加驱油效率,在低渗透油藏提高采收率方面具有广阔的应用前景[5-7]。但与连续注气、注水相比,水气交替驱注入能力发生异常的可能性明显增加,由于水的流度相比于CO2相对较小,注水能力的降低显得尤为突出[8]。就目前国内外已开展的CO2水气交替驱矿场项目,注水能力的降低已成为制约水气交替驱提高采收率的关键因素之一[9-10]。针对水气交替驱注入能力的预测与评价问题,国内外学者已开展了一些研究,但大多借助于试验手段,分析CO2水气交替注入过程中注入能力变化规律[11-17]。对于理论研究,已建立的数学模型中未能充分考虑CO2与原油、注入水之间的相互作用。为此,笔者根据以上研究中理论模型存在的不足,基于传统的B-L方程,考虑CO2、原油及注入水之间的相互作用,通过对气驱油及水驱气过程中的B-L方程进行修正,并结合多重复合油藏渗流理论,建立CO2水气交替驱数学模型,以此分析地层润湿性、CO2-原油界面张力及渗透率等对水气交替注入过程中注水能力的影响。

1　CO2水气交替驱模型

1.1　物理模型

研究的CO2水气交替驱模型驱替形式为先注CO2后注水,CO2与原油非混相,但存在相互作用,对模型做出以下基本假设:①圆形地层、水平、均质、等厚,外边界封闭,上下有不渗透隔层,中心有一口注入井,定流量注入CO2/水;②考虑CO2在原油、注入水中的溶解及CO2对原油的抽提作用;③流体微可压缩,流动过程等温,流动服从达西定律,忽略毛管力与重力分异作用的影响。CO2水气交替注入所形成的饱和度剖面如图1所示。Ⅰ区为水区,Ⅱ区为CO2-水过渡区,Ⅲ区为CO2区,Ⅳ区为饱和CO2的原油与饱和油组分的CO2所形成的CO2-原油过渡区,Ⅴ区为未波及原油区。

1.2　修正的B-L方程

CO2水气交替注入过程可分为CO2驱油与水驱CO2两个独立的阶段,因此可应用Buckley-Leveret理论求得气驱油及水驱气过程中前缘的移动速度。但考虑到CO2在油、注入水中的溶解及油组分在CO2中的挥发,必须对B-L方程加以修正。以一维CO2非活塞式驱油模型为例,分流量形式下CO2组分物质的量浓度守恒式[18-21]为

(1)

其中

CCO2=SgCCO2,g+(1-Sg)CCO2,o,

FCO2=fgCCO2,g+(1-fg)CCO2,o,

TD=qBt/φAL,xD=x/L.

式中,CCO2为CO2在气相和油相中的总物质的量浓度,mol/L;FCO2为总的CO2组分流量,mol/L;TD为无因次注入时间;xD为无因次距离;CCO2,g和CCO2,o分别为CO2在油、气相中物质的量浓度,mol/L;Sg和fg分别为CO2饱和度、分流量;q为流体注入速率,m3/d;B为流体体积系数;φ为地层孔隙度;A为渗流截面积,m2;x为流体渗流长度,m;L为一维地层长度,m;t为流体注入时间,d。

图1　CO2水气交替驱饱和度剖面示意图Fig.1　Schematic of saturation profile for CO2water-alternating-gas flooding

式(1)为一维拟线性方程,可运用特征线法进行求解[22],其特征方程为

(2)

因dCCO2/dTD=0,故特征线方向上的CO2物质的量浓度为常数,由此可得等CO2物质的量浓度剖面移动速度vCCO2表达式为

(3)

CO2驱油的前缘与尾部存在CO2物质的量浓度跳跃,移动速度可近似转换为差分格式为

(4)

根据式(4)可推导CO2驱油前缘与尾部移动速度vCCO2,Ⅳ-Ⅴ和vCCO2,Ⅲ-Ⅳ分别为

(5)

(6)

(7)

忽略束缚水的影响,在Ⅲ区最大含气饱和度下fg=1。CO2驱油前缘、尾部移动速度可根据式(5)、(6)用图解法求解(图2)。图2中线① 、②的斜率即代表前缘与尾部移动速度。

图2　CO2驱油分流量曲线Fig.2　Fractional flow curve for CO2displacing oil

公式(5)、(6)求取的是基于一维线性流的前缘与尾部移动速度,对于平面径向流,移动速度表达式须做出适当变换:

(8)

式中,r为地层半径,m;h为地层厚度,m。

对式(8)分离变量并积分:

(9)

式中,R为流体渗流半径,m;rw为井径,m。

由于rw较小,忽略其影响,同时对式(9)无因次化:

(10)

其中

RD=R/rw.

对于CO2驱油与水驱CO2过程,TD有不同的表达式,分别为

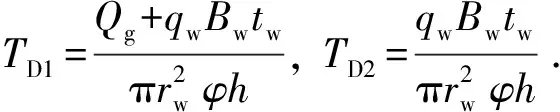
(11)

式中,TD1为无因次CO2与水累积注入体积;TD2为无因次累积注水体积;Qg为CO2总注入量,m3;qw为注水速率,m3/d;Bw为注入水体积系数;tw为注水时间,d。

分别联立式(10)与式(5)、(6),求得不同时刻下气驱油前缘与尾部无因次半径RⅣ-Ⅴ与RⅢ-Ⅳ分别为

(12)

对于水驱CO2,忽略残余油的影响,运用与CO2驱油类似的方法可以得到其前缘、尾部移动速度(vCCO2,Ⅱ-Ⅲ、vCCO2,Ⅰ-Ⅱ)与无因次半径(RⅡ-Ⅲ、RⅠ-Ⅱ),分别为

(13)

(14)

(15)

(16)

因不考虑水在CO2中的扩散,Ⅱ区右端面与Ⅲ区左端面中CO2物质的量浓度相同,即DⅡ-Ⅲ为1。与CO2驱油前缘、尾部移动速度求取方法类似,水驱CO2移动速度亦可运用图解法求解(图3)。线③ 、④的斜率即为水驱气过程中形成的前缘与尾部的移动速度。

图3　水驱气分流量曲线Fig.3　Fractional flow curve for water displacing gas

综合图2、3分析,直线③的斜率明显大于②,即水驱CO2前缘快于CO2驱油尾部的移动速度,因此随注入水量的增加,两者会发生交汇,此时情况较为复杂,超出本文的研究范围,本文中仅研究两者交汇之前的驱替过程。

1.3　数学模型

基于图1所示的CO2水气交替驱物理模型,应用多重复合油藏渗流理论[23-24],考虑表皮系数和井筒存储的影响,建立外边界封闭条件下的无因次数学模型为

(17)

(18)

(19)

(20)

其中

λw=kKrw/μw,λg=kKrg/μg,λo=kKro/μo,

Ct1=SwCw+SorgCo+SgrCg+Cr,

Ct3=SgCg+SwcCw+SorgCo+Cr,

Ct5=CwSwc+SoCo+Cr.

为对模型进行求解,需给出模型的初始及边界衔接条件。

初始条件为

pD1=pD2=pD3=pD4=pD5=0 (tD=0) .

(21)

内边界条件为

(22)

式中,CD为无因次井筒储集系数;S为表皮系数;pwD为无因次井底压力。

外边界条件为

(23)

衔接条件为

(24)

2　模型的求解与验证

2.1　修正B-L方程求解

由1.2节中的叙述可看出,渗流扩散阻滞系数等参数需在CO2驱油、水驱CO2饱和度剖面已知后才能得以确定,因此首先要根据改进的CO2驱三相相对渗透率Corey模型[25]得到气驱油及水驱气相对渗透率:

(25)

(26)

式中,Sgc为束缚气饱和度;Krog和Krgo分别为CO2驱油过程中油、气的相对渗透率;nrog和nrgo分别为Corey油、气相渗指数,取值为2～4;Krwg和Krgw分别为水驱CO2过程中水、气相对渗透率;nrwg和nrgw分别为Corey水、气相渗指数,取值为2～4。

已知CO2驱油及水驱气相对渗透率,可得其分流量曲线;根据Buckley-Leveret理论,运用图解法可得到CO2驱油前缘含气饱和度,假定尾部处为最大含气饱和度,在一定的温度、压力及原油组成下,进行闪蒸平衡计算[26-27],将得到的油相与气相中CO2浓度代入式(7),即可求得DⅣ-Ⅴ与DⅢ-Ⅳ。

试验研究显示CO2在水中溶解浓度与压力、温度满足关系式[28]:

(27)

式中,R为CO2在水中的物质的量分数;p为压力,MPa;T为温度,K;C00=1.87×10-2,C01=-4.67×10-5,C10=4.54×10-4,C11=-4.54×10-7。根据式(27)计算结果即可求得CO2在水中的扩散浓度,代入式(15),进而得到DⅠ-Ⅱ。

已知DⅣ-Ⅴ、DⅢ-Ⅳ与DⅡ-Ⅲ、DⅠ-Ⅱ,运用图解法(图2、3)可得到气驱油及水驱气前缘、尾部移动速度,分别代入式(12)与式(16),可求得不同注入时刻各区半径,并带入数学模型,实现修正B-L方程与复合油藏模型的耦合。

2.2　数学模型的求解

将建立的数学模型进行拉氏变换,得到关于rD的虚宗量Bessel函数通解为

(28)

式中,s为拉氏变量。代入边界及初始条件,构建系数矩阵方程组,可求得待定系数a1～a10的值。则井底压力拉氏空间解为

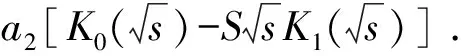
(29)

对式(28)进行Stehfest数值反演[29],可计算出每一个无因次时间tD所对应的无因次井底压力,同时进行有因次化,即可得到注水时实际井底注入压差,以此反映注入能力的变化规律,注入压差越大,表明注入能力越小。

2.3　模型的验证

为验证所建CO2水气交替驱模型的正确性,参考SL油田实际地层及流体特性,设定储层及流体物性参数,其中油藏半径为1 000 m,地层厚度为10 m,孔隙度为15%,渗透率为0.01 μm2,平均地层压力为16 MPa,地层温度为70 ℃,束缚水、残余油、气驱油束缚气及水驱气滞留气饱和度分别为35%、12.5%、7.5%和12.5%,注入水、CO2地下黏度分别为0.27和0.040 5 mPa·s,注入水、岩石、原油与CO2压缩系数分别为4.5×10-4、4×10-4、2.6×10-3和4.5×10-2MPa-1,注入水体积系数为1.0;对于注入井生产制度,日注气量和注水量分别为30和10 m3/d,注气和注水时间分别为300和100 d,井径为0.1 m,井储和表皮均设为0;原油组分组成如表1所示。将上述参数代入建立的模型计算,可求取注入压差,同时依据上述参数,可建立CO2水气交替驱油藏数值模拟组分模型。

表1　原油组分组成

图4　本文中模型与数值模拟结果对比Fig.4　Results comparison between analytical model and numerical simulation

设置地层渗透率分别为0.005、0.01和0.02 μm2,对比本文中建立模型与数值模拟模型注水过程中压差变化(图4),可看出本文中模型与数值模拟结果整体拟合程度较好,验证了所建立模型的准确性,但由于在一般的CO2水气交替数值模拟中未考虑CO2在注入水中的溶解,因此造成数值模拟与本文中模型结果在初期存在偏差。因CO2在水中的溶解量较少,随注水量增加,CO2溶解作用对注入压差影响程度不断减小,曲线拟合程度变好。此外,还可发现地层渗透率越小,注入压差越大,且注入压差增大程度随渗透率的减小而增加,表明存在渗透率界限使注入能力与驱替效果达到最优。

3　注入能力影响因素分析

低渗透油藏储层及流体性质的差异是造成注水能力下降的原因之一,分析储层润湿性状况、CO2-原油界面张力及地层渗透率对注入能力的影响。

3.1　润湿性

不同的沉积状况会造成油藏岩石呈现不同的润湿性。对于地层润湿性的类型,可通过测量油藏流体与岩石间的接触角判断,但该方法测量过程较为复杂,且难以准确测定。在实际的矿场应用中,可通过观测相渗曲线等渗点的移动,近似描述岩石润湿性的变化[30]。通过给定不同的相渗指数,得到不同的相渗曲线(图5),以此模拟不同润湿性地层下的CO2驱油及水驱气的过程。

图5　不同润湿性地层CO2驱油及水驱气相渗曲线Fig.5　Relative permeability curves of CO2 displacing oil and water displacing gas for reservoirs with different wettability conditions

润湿性不同使气驱油及水驱气相渗曲线的等渗点左右移动。对于偏水湿岩石,气驱油及水驱气相渗曲线的等渗点明显偏右,而偏油湿岩石则偏左,中性润湿岩石介于两者之间(图5)。在不同润湿性下井底注入压差呈现不同的变化规律(图6)。由于岩石润湿性的差异,对于偏水湿地层,在毛管力的作用下,注入水首先进入小孔隙中,大量的CO2被圈闭在大孔隙中,使水的注入压差较大,注入能力较低;相反,对于偏油湿地层,注入水率先进入大孔隙中,对CO2形成较为均匀的驱替,使注入压差较小,注入能力相对较大。

图6　不同润湿性地层注入压差随时间变化Fig.6　Pressure drop versus time for formations with different wettability

3.2　CO2-原油界面张力

由于不同油田区块原油组成存在差异,使在相同注入条件下CO2与原油间界面张力并不相同。研究表明,在不同油气界面张力下,油气相渗曲线会发生规律性变化[31]。为探究不同油气界面张力对注入能力的影响,假设水驱气过程相对渗透率保持恒定,改变气驱油相渗指数,得到不同油气界面张力下油、气相对渗透率曲线(图7)。

图7　不同界面张力下CO2驱油相渗曲线Fig.7　Relative permeability curves for different interfacial tensions between oil and gas

对图7进行分析,可发现对于不同界面张力下的相渗曲线,等渗点所对应的含气饱和度近似相同,表明润湿性变化对注入能力的影响可忽略。不同界面张力下注入压差随时间变化如图8所示。由图8可看出,由于在低界面张力下CO2溶解度增大,使原油流动能力增强,井底注入压差减小,注入能力增加,但总体差距较小,说明界面张力的减小对于注入能力的提高影响程度有限。当原油密度、黏度相差不大时,原油组成不同对后续注水过程中注入能力的影响较小。

图8　不同界面张力下注入压差随时间变化Fig.8　Pressure drop versus time for different interfacial tensions

3.3　渗透率界限

图9　不同渗透率地层注水100 d后注入压差Fig.9　Pressure drop for formations with different permeability after injecting water for 100 d

对于低渗透油藏,注入能力对渗透率的变化反应较为敏感。为更清晰地显示注入能力随渗透率的变化规律,绘制不同渗透率下注水100 d后的井底注入压差变化曲线(图9),可发现当渗透率小于5×10-3μm2时,井底注入压差随渗透率的减小而急剧增大,表明注入能力迅速减小,因此在矿场实践中,对于渗透率小于5×10-3μm2的地层,在开发之初要充分考虑渗透率对后续注水能力的影响。

4　结　论

(1)考虑CO2在原油、注入水中的溶解及CO2对原油中轻质组分的抽提作用,对B-L方程进行修正,并结合多重复合油藏渗流理论,建立封闭油藏CO2水气交替驱注入能力数学模型,与数值模拟结果对比,验证了模型的有效性,为低渗透油藏CO2水气交替驱注入能力的预测奠定了基础。

(2)地层润湿性对后续水驱注入能力影响较大,相比于偏油湿地层,在偏水湿地层中,由于注入水对CO2的圈闭作用,使注入能力较小;后续水驱注入能力随CO2与原油间界面张力的减小而增加,但其对注入能力的影响程度相对较小。

(3)对于低渗透油藏,当油藏渗透率低于5×10-3μm2时,在进行CO2水气交替驱方案设计之初,要对水气交替注入能力进行评价,考虑到注入能力的变化对方案可行性的影响,制定合理的注入方案和工艺措施。