一种面向3D打印技术的STL模型快速分层算法

江本赤，王建彬，王　刚

（安徽工程大学 机械与汽车工程学院，安徽 芜湖241000）

3D打印是以数字模型文件为基础，可将设计理念快速、准确地转换为具有一定功能原型的技术［1］。大多数3D打印系统都是先建立CAD模型，再设定精度将CAD模型转换为STL模型，然后对STL模型进行切片处理。切片处理是3D打印中的重要步骤，切片处理后生成的一系列二维封闭多边形轮廓是3D打印的基础。STL文件存在多种缺陷，如：在记录三角形顶点坐标信息时存在冗余；在将CAD模型转换为STL模型时，存在精度损失，且精度损失越小，STL文件越大；存在信息缺乏、三角形间无任何拓扑关系等。这些造成了STL模型切片算法效率较低，但因为STL文件生成简单、输出广泛适用、易于切片处理等优点，所以对STL模型切片算法研究仍然是研究的主流［2-4］。

目前，研究人员已提出了多种STL模型切片算法。如：王素等［5］采用邻接插入法建立三角形间的邻接关系，根据三角形顶点坐标反求与该三角形相交的切片平面，利用已经建立的三角形间邻接关系获取有序的交点，完成对STL模型的切片；田明海［6］建立层变边数组与初始层数的邻接边顺序链表，利用层变边数组与初始层数的邻接边链表进行断链与合链操作，求取下一层的邻接边顺序链表，进而建立整体的邻接边顺序链表，完成对STL模型的切片；黄丽［7］首先建立与当前切平面相交的三角形集合，然后根据交点间的冗余特性构建三角形间的拓扑关系，完成对STL模型的切片；钟山等［8］首先设定角度阈值并求取垂直切片轮廓线的点切线与水平分层面的切线角，然后比较角度阈值与切线角的大小决定分层的厚度，最后利用三角形的邻接关系完成对STL模型的切片；Zhang等［9］建立与切平面相交的三角形集合，将每个三角形与切片平面相交的两条边设定为前边与后边，利用前边与后边的关系重建拓扑关系，获得邻接边顺序链表，完成对STL模型的切片。

考虑到STL模型存在冗余信息，我们在吸收上述算法优点的基础上，提出了一种STL模型快速切片算法。在读取STL文件时，确定STL模型中与每层切片平面相交的三角形，将三角形索引值和三条边存入切片面结构数组，将三角形与切片平面相交的两条边、与边所属的三角形面片的索引值存入每层切片平面的切片边结构数组。根据每层切片边数组中的三角形信息，利用逐边识别与剔除的思想和相邻切片层间的三角形拓扑关系具有继承性的特点重建拓扑关系，将建立完成的拓扑关系和求出的交点坐标依次存入有序边点数组中。从有序边点数组中获取有序交点并依次连接得到二维封闭轮廓。

1　STL文件信息存储特点

STL文件格式是由美国3D SYSTEMS公司于1988年制定的［1］。STL模型由CAD模型表面三角化处理生成，但转换成STL模型后其原有的拓扑关系会丢失。STL文件中每个三角形的定义都包括以逆时针顺序记录的顶点坐标与指向模型外侧的单位法向量。

STL文件有两种格式：二进制格式与ASCII格式。二进制采用固定字节给出三角形面片的几何信息，ASCII格式以关键字为标志逐行给出三角形面片的几何信息。由于ASCII格式比二进制格式更具可读性和直观性且方便对数据做进一步处理，在对STL模型进行分层时，普遍选择STL文件的ASCII格式，如图1所示。

图1　STL文件的ASCII格式结构

2　STL模型分层算法

对STL模型进行分层时，其分层方向一般选取与z轴平行的方向。

2.1　STL文件的处理

在读取STL文件时，建立分层面结构数组存储STL文件中记录的三角形数据，该数组包含三角形面片的索引值和三角形的边，其中每条边的顶点坐标都按照z坐标值的升序排列。在建立分层面结构数组的同时，也针对每个分层平面建立分层边结构数组，该结构数组包含三角形与分层平面相交的两条边及与边所属的三角形面片的索引值。这里，三角形两条边中任意一条若是首次与切平面相交则被记录，不是则不被记录；若三角形的一条边在切平面上，则记录另外两条首次与分层平面相交的边，整个三角形在切平面上不会被记录。

如图2所示，任意给定一个三角形Tk（k=1，2，…，m）， 该三角形三个顶点坐标分别为 Vkmin（xk1，yk1，zkmin）、Vkmid（xk2，yk2，zkmid）和 Vkmax（xk3，yk3，zkmax），其中 zkmax≥zkmid≥zkmid，在分层面数组中的记录形式为［Tk，Sk1（Vkmin，Vkmid），Sk2（Vkmid，Vkmax），Sk3（Vkmin，Vkmax）］。假设与三角形 Tk相交的分层平面分别为 Layer（i）、Layer（i+1）和 Layer（i+2）（i=1，2，…，n-2）。 在 Layer（i）分层中，三角形的两条边 Sk1和 Sk3首次与 Layer（i）分层平面相交，因此它们在 Layer（i）的分层边数组中记录方式为［Tk，Sk1（Vkmin，Vkmid），Sk3（Vkmin，Vkmax）］；在 Layer（i+1）分层中，三角形的两条边 Sk1和 Sk3与 Layer（i+1）分层相交，但并不是首次与切平面相交，因此它们在Layer（i+1）的分层边数组中不记录；在 Layer（i+2）分层中，三角形的两条边 Sk1、Sk2中 Sk2首次与 Layer（i+2）分层平面相交，因此它们在Layer（i+2）的分层边数组中记录方式为［Tk，Sk2（Vkmid，Vkmax），Sk3（Vkmin，Vkmax）］。

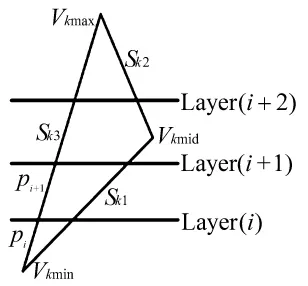
图2　三角形与分层平面相交示意图

2.2　交点的计算

在STL模型的分层算法中，高效获取各三角形与分层平面的交点数据可以提高分层算法的效率。设图2 中三角形 Tk的 Sk3边与 Layer（i）和 Layer（i+1）分层平面的交点分别为点 pi（xi，yi，zi）和 pi+1（xi+1，yi+1，zi+1），根据边Sk3的直线方程

可得点 pi（xi，yi，zi）坐标

同理可得点 pi+1（xi+1，yi+1，zi+1）坐标

其中：zi为 Layer（i）分层平面的高度，zi+1为 Layer（i+1）分层平面的高度。

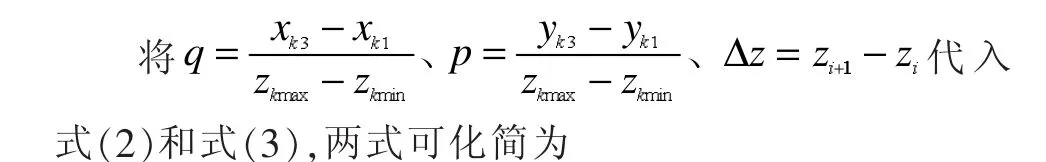
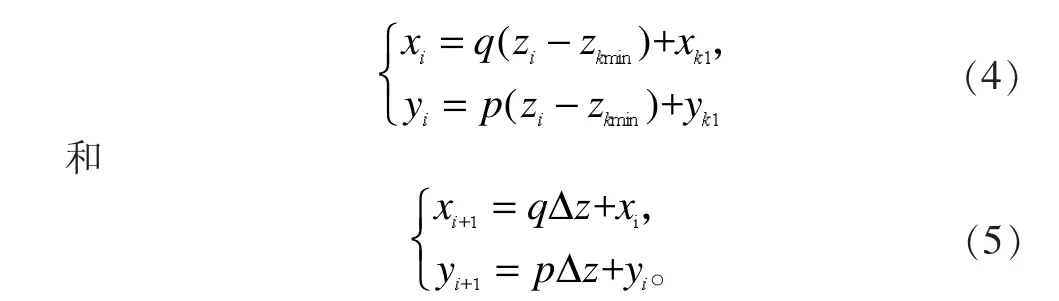
若三角形的某一条边首次与切平面相交，则利用式（4）求出交点坐标；若该边再与其他切平面相交，则利用式（5）求出交点坐标。该方法简化了交点的计算，提高了分层效率。

2.3　拓扑关系的重建

因为在CAD模型转换为STL模型时丢失了原有的拓扑关系，所以STL文件中记录的三角形毫无顺序。为了获取有序的交点，需要重建三角形间的拓扑关系。我们根据STL模型本身的冗余信息，利用逐边识别与剔除的思想及相邻分层间的三角形拓扑关系具有继承性的特点重建拓扑关系。如图3所示，根据STL文件的冗余信息，三角形T1与三角形T2共用一条边，可得到S13=S23。因此，利用三角形T1的边S13可快速查找到三角形T2，重建三角形间的拓扑关系。

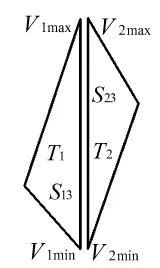
图3　冗余信息示意图

三角形间的拓扑关系可以分为简单拓扑关系与特殊拓扑关系，如图 4 所示。 在图 4（a）中，与 Layer（i）、Layer（i+1）和 Layer（i+2）分层平面相交的三角形没有改变，因此不需要建立 Layer（i+1）及 Layer（i+2）分层平面相交三角形间的拓扑关系，可以继承已经建立的与Layer（i）分层平面相交三角形间的拓扑关系。在图 4（b）中，与 Layer（i）、Layer（i+1）分层平面相交的三角形发生改变，需要重新建立与Layer（i+1）分层平面相交三角形间的拓扑关系。在Layer（i）分层平面中，已经建立的三角形间的拓扑关系为［T1，T3，T5，T7，T8］，则在建立与 Layer（i+1）分层平面相交的三角形间的拓扑关系时，先在Layer（i）分层的三角

扑关系中删除与Layer（i+1）分层平面不相交的

形，标记只有一条边与Layer（i+1）分层相交的三角形，得到［T1，T8］，再获取 Layer（i+1）分层平面的分层边数组信息［T1，T4，T2，T6，T8］，最后根据该信息重新建立Layer（i+1）分层中三角形间的拓扑结构［T1，T4，T2，T6，T8］。STL 模型中与 Layer（i+1）、Layer（i+2）分层平面相交的三角形并没有改变，因此Layer（i+2）分层三角形拓扑关系可继承Layer（i+1）分层的三角形间拓扑关系。

拓扑关系重建算法步骤如下。

Step1：读取Layer（1）分层的分层边数组信息。

Step2：任意获取Layer（1）分层边数组中的一个三角形Tk，以该三角形与切平面相交的一条边Sk1遍历整个Layer（1）分层边数组，找到三角形Tk的邻接三角形然后将有关三角形Tk与的信息从Layer（1）分层边数组中删除，同时将相交边与交点数据存入有序边点数组，如其中，Ik与为通过式（4）计算出的边Sk1、与分层平面的交点。

Step4：读取 Layer（i）（i=2，3，…，n）的分层边数组信息，在Layer（i-1）分层三角形拓扑关系中删除与Layer（i）分层平面不相交的三角形，标记只有一条边与Layer（i）分层平面相交的三角形，交点信息通过式（5）进行更新。

Step5：在 Layer（i）的分层边数组中找到与标记三角形对应的三角形索引值，以该三角形为Tk，对于任意第Layer（i）分层，利用上述方法进行拓扑重建，直至找到另一个标记三角形（即与Layer（i）分层平面相交但尚未记录在Layer（i）分层边数组中的三角形），利用所继承Layer（i-1）分层内的拓扑关系，获取封闭二维轮廓。

Step6：判断 Layer（i）的分层边数组是否为空，若不为空，则说明存在其他封闭轮廓，依次利用上述方法直至Layer（i）的边数组为空，获取该层内所有的封闭轮廓。

图4　拓扑关系

2.4　有序交点的获取与连接

完成拓扑关系重建之后，从有序边点数组中获取有序交点并依次连接，即可形成封闭的二维截面轮廓。如图5所示，对于Layer（t）分层平面，建立的有序点边数组为获取的有序交点数组其中I1=I3。舍弃重复的坐标值I3，将有序交点坐标值依次进行连接，形成封闭的二维截面轮廓。

图5　生成有序交点序列

3　实例验证

以图6所示的某法兰STL模型为例，检验算法的分层效果。该模型具有较复杂的几何结构，有助于评判复杂二维截面轮廓的正确性。

利用本算法对图6中的STL模型进行分层，获得了图7（a）所示的分层效果，图7（b）为其中一个层片的二维轮廓情况。由图7可以看出，分层模型可清晰地包络出原始STL模型，其中的一个层片亦完全符合模型的局部几何特征，这验证了算法的有效性和可行性。

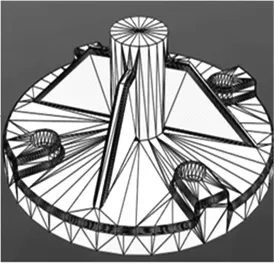
图6　某法兰的STL模型

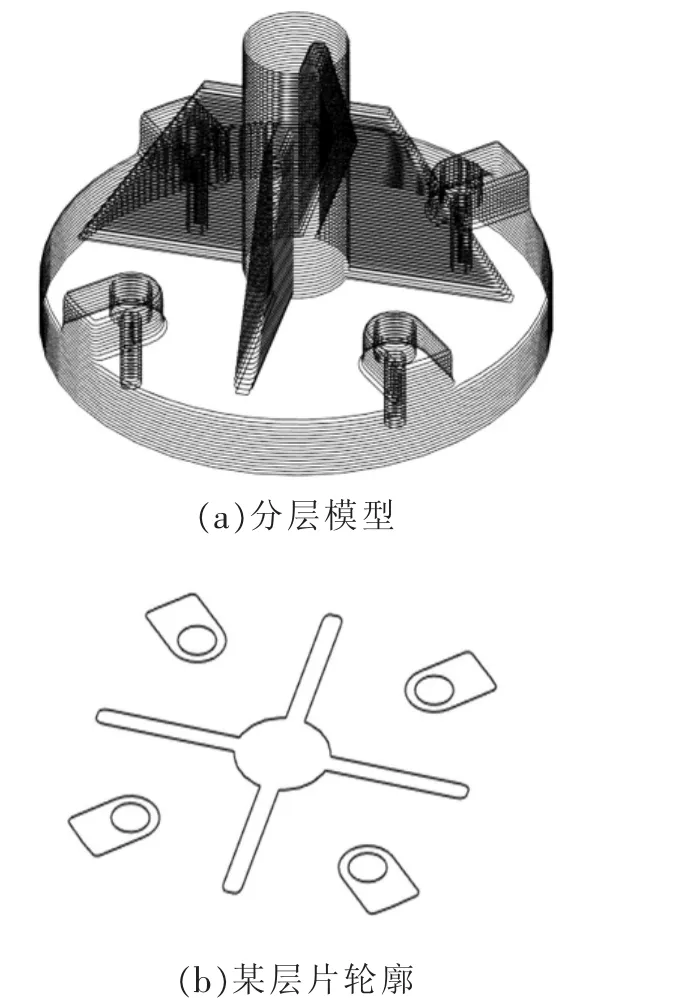
图7　模型分层效果

4　结论

基于STL模型文件信息的冗余特性分析，通过判断三角形各边的共用情况，建立了相应的拓扑关系，并获取了封闭的二维轮廓，进而实现了对STL模型的分层操作。通过对一个典型模型的分层实验证实了该算法可行性。通过以上研究工作可以得出以下结论：

（1）在读取STL文件的同时，确定STL模型中与各分层平面相交的三角形集合，有利于减少三角形与分层平面间位置关系的判断次数。

（2）在求三角形与分层平面间的交点时，利用相邻层片交点间的关系，可快速获取交点坐标，并可避免分层交点的重复计算。

（3）基于逐边识别与剔除的思想建立拓扑关系，利用拓扑关系的继承性，可减少遍历次数，有效提高计算效率。