一种改进的DWT-FMM图像修复算法

补朝阳，李　尊

（1.新乡学院 a.化学化工学院；b.物理与电子工程学院，河南 新乡 453003；2.武汉科技大学 信息科学与工程学院，湖北 武汉430081）

图像修复技术［1-2］用来对破损图像的待修复区域进行合理的填充，恢复视觉效果。目前，此技术已被应用于文物修复、旧照片恢复、冗余目标移出等方面，是图像处理与计算机视觉领域的研究热点。国内外的研究者提出了许多种修复方法，如基于变分和偏微分法、基于等照度线扩散法、基于纹理合成法、混合法以及变换域法等。基于小波变换的图像修复［3］算法进行逐点计算，保证修复质量和效率。康佳伦等［4］提出引入梯度直方图进行方向筛选的方法较好地保留了修复边缘。Hung等［5］提出的贝赛尔曲线逼近边缘方法保证了对曲线结构的较好修复。

在本文中，我们提出改进的DWT-FMM图像修复算法是对Eikonal方程和权重函数进行改进，引入约束最小二乘法进行滤波，在保证修复效率的基础上，提高细节修复效果。

1　小波变换

小波变换［6］是频域的变换方法，此方法在时域和频域均具有良好的局部化特性。设C0表示原始图像，离散小波变换如下：

其中：m=0，1，…，m-1；h、v 和 d 分别表示水平分量、垂直分量和对角分量；G和H都是小波变换中滤波器系数矩阵，’表示H的共轭转置矩阵，表示G的共轭转置矩阵。小波重构表达式为

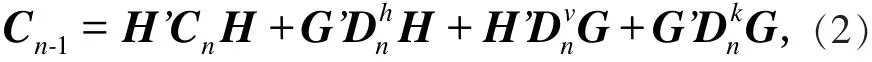
其中 n=N，N-1，…，1。

2　DWT-FMM图像修复算法

DWT-FMM图像修复算法对待修复图像进行小波变换，得到低频图像和高频图像。算法对低频图像以点为单位，采用FMM（fast marching method）方式进行匹配，逐步修复图像；对高频图像，则利用小波分解后上下层之间的关联性进行预测。为了使修复图像的效果更自然，我们对修复的图像使用维纳滤波。

2.1　低频图像修复

低频图像以像素点为研究对象，采用FMM算法对待修复区域由外向内逐步推进修复，直至待修复区域修复完成。

FMM算法［7］由Telea于2004年提出，其实质是利用 Eikonal方程求解时间达到函数 T（x，y），模拟曲线进化过程来完成修复。此修复方法是由待修复区域边缘逐渐向里推进，保证离完好区域最近的像素点优先得到修复，与人工修复原则一致。FMM算法模型如图1所示。在图1中，表示待修复区域，Ψ表示完好区域，∂表示待修复区域边界，P表示待修复像素点，Nξ（P）表示邻域像素点集合。

图1　FMM算法模型

FMM算法将像素点分为3类，分别是未知像素点、已知像素点和边界像素点。T（x，y）可通过Eikonal方程

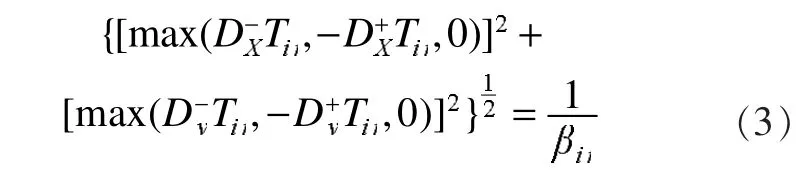
求解。在式（3）中：βij表示待修复像素点法向运动速率，取值为1；表示一阶有限差分形式。

为了保证修复路径正确，及待修复像素点灰度值匹配正确，需要在待修复像素点P的周围建立数学模型，计算邻域像素点q对点P影响，进而计算出点P的灰度值。计算方法如下：

式（4）表示在点P的修复中，权重函数占主导地位。此方程式保证在修复的过程中保留完好区域的结构特征。式（5）表示权重函数由3个因子所决定，分别是方向因子r、距离因子t和水平集因子V，即

式（6）中：方向因子r表示像素点q与像素点P纹理越相似，权重值越大；距离因子t表示像素点q与像素点P距离越近，权重值越大；水平集因子V表示像素点q的更新时间越短，权重值越大。

低频图像的修复依照FMM算法进行，直至待修复区域修复完成。

2.2　高频图像修复

高频图像修复要通过低频信息进行预测，首先剔除高频图像待修复区域的边界，然后对低频已修复好的区域进行水平、垂直和对角方向滤波，并填充至高频待修复图像中，最后采用维纳滤波处理使修复效果更加自然。

3　改进的DWT-FMM图像修复算法

我们提出的改进的DWT-FMM图像修复算法针对Eikonal方程和权重函数进行了改进，图像自然化滤波则采用约束最小二乘法。

3.1　Eikonal方程改进

在式（3）中，有限差分的形式为一阶。文献［8］针对FMM算法的精度进行分析，得出二阶差分精度高于一阶差分精度的结论。因此我们用二阶差分的形式替代一阶差分引入Eikonal方程，改进DWT-FMM图像修复算法，完成图像修复操作，表达式如下：

上述4个表达式为二阶差分形式，其中Δx和Δy分别表示在x轴和y轴方向上的网格间距，Ti，j表示网格坐标（i，j）的到达时的值。

3.2　权重函数的改进

权重函数是由方向因子、距离因子和水平集因子的乘积形式决定的，具有盲目性。在权重函数表达式中，3个因子对函数的影响应具有同等地位，而在图像修复的原则中，方向因子的优先级要高于其余2项，否则易引入相关度较小的像素点，影响修复效果。为此，我们提出将黄金率［9］引入权重函数中，将因子相乘形式改成加权和的形式，以此提高方向因子的优先级，保证修复按照图像结构的方向进行，符合图像修复的要求。改进的权重函数表达式为

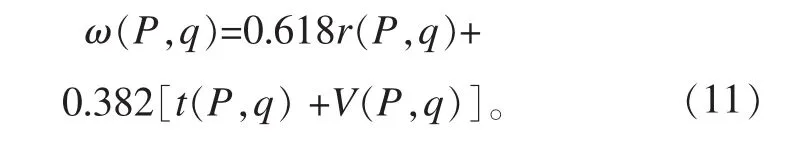
3.3　约束最小二乘法

原修复算法的最后步骤是采用维纳滤波进行自然化处理。维纳滤波是由Winner提出的，具有计算量小、抗噪能力强和修复效果好的特点，在图像复原中被广泛应用。但是图像修复是一个病态的逆问题，为了克服病态，我们采用约束最小二乘法［10］进行自然化处理。此方法可利用待修复图像的先验知识进行约束，提高修复质量。我们采用MATLAB中的deconvreg函数进行约束最小二乘法处理，其中拉格朗日算法的搜索范围是 10-9～109。

4　仿真实验结果

仿真实验对算法的整体及所有改进部分都进行对比。实验软件采用MATLAB 7.0，客观参数有均方误差MSE、峰值信噪比PSNR和修复时间t。结果如图2所示。图2a）为原图，图2b）为待修补图像（其中待修复区域用数字标注，便于对比），图2c）为原算法修复图，图2d）为Eikonal改进修复图，图2e）为权重函数改进修复图，图2f）为采用约束最小二乘法滤波的修复图，图2g）为本文算法修复图。

针对Eikonal改进进行对比，如图2c）和图2d）所示。人眼看到的修复效果是，图2c）中明显有修复痕迹，而图2d）的修复痕迹减轻，特别是在1处（Lena帽子上方的拐角部分），图2d）细节处理效果较好，基本恢复原图信息，满足修复要求。客观结果如表1所示，Eikonal改进算法提高了修复的质量和修复效率，此改进具有一定价值。

针对权重函数改进进行对比，如图2c）和图2e）所示。从人的视觉出发，图2c）和图2e）相差不大，基本满足人的视觉要求，无明显错误信息的修复，但均存在一定程度的修复痕迹。客观结果如表1所示，权重函数改进算法的图像质量具有一定的提高，修复时间也较原算法有所降低。

针对不同的滤波方法修复图进行对比，如图2c）和图2f）所示。从人的视觉出发，图2f）的改进效果与图2c）没有明显差别。但从客观数据表1可得出，无论是修复质量还是修复效率，本算法都得到了一定的提高，相较于维纳滤波可以达到自然修复的目的。

对改进算法和原算法进行对比，如图2c）和图2g）所示。改进算法在细节处理上有一定程度的提高，减少了修复痕迹，得到了修复效果更好的修复结果图，符合修复的原则。客观结果如表1所示，改进算法在提升图像修复质量、满足视觉要求和加强细节处理的基础上，保证了效率。

图2　修复效果对比图

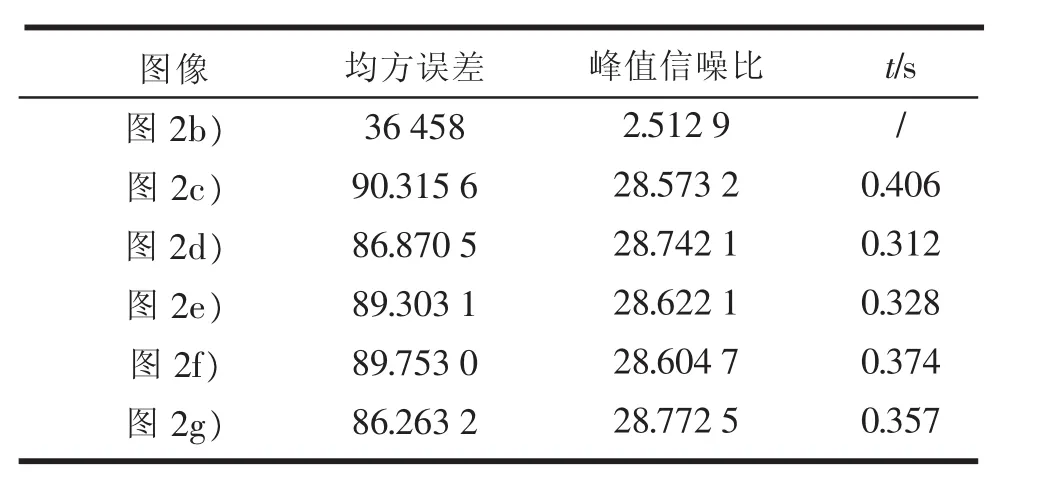
表1　客观数据对比表

5　结束语

在DWT-FMM修复算法的基础上，针对3方面进行改进：改进的Eikonal方程提高修复精度，改进的权重函数保证修复图像的结构方向和改进滤波方法增强修复的自然效果。改进算法在细节修复上有一定提高，人为修复痕迹减轻，修复效果自然，但仍存在条状痕迹。综上，改进算法对图像的细节修复具有一定的参考意义。下一步将以修复边缘为对象进行研究，降低修复痕迹的视觉效果。