基于分形理论的图像边缘特征提取算法

冯学晓，古险峰

（郑州工业应用技术学院 信息工程学院，河南 郑州 451100）

图像边缘是指图像灰度发生剧烈变化的区域，描述了图像信息的某种不连续性，标志着不同区域间的接合，边缘特征提取是指提取出目标图像与背景间的边界［1］。利用图像边缘灰度值变化大的特征，得到不同类型图像的分类效果，从而在保留图像特征信息的同时，减少数据的冗余。传统的边缘检测算法容易受到噪声影响，利用滤波去噪又会引起边缘模糊，而分形检测具有对噪声不敏感的特点，如将传统边缘检测算法与分形理论相结合，得到图像边缘的几何特征，则可方便地对图像进行有效的处理和分析［2］。

1　分形维数

1.1　分形理论

传统的几何理论针对的是规则的光滑的几何结构，只能描述处处连续的处处可微的曲线，而在实际应用中，大部分结构都是不规则的，不具有可微性［3］。分形作为几何学的研究对象，具有自相似性，针对的是不规则的破碎形状。在欧氏几何中，维数以整数的形式存在，点是零维的，线是一维的，面是二维的，立体是三维的。而在分形理论中，分形维数越小，图像纹理越平滑；分形维数越大，图像纹理越粗糙。同时，由于边缘不规则，图像的拓扑维数要小于图像的分形维数。因此，分形维数不是整数而是分数，可以详细地描述事物的“不规则程度”［4］。分形维数的数学定义是：设在δ尺度下，当δ→0时，测量平面曲线F的分形维数P具有以下规律：

忽略小于 δ 尺度的不规则边缘，对式（1）两边同时进行对数运算得

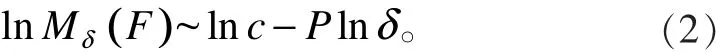
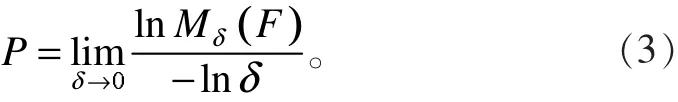
1.2　常用分形维

（1）盒维数。盒维数是分形维数最简单的表示形式，也叫熵维、度量维和信息维［5］。盒维数的定义为：假一个有界集合，在欧几里得距离下，将图形划分为若干个大小和形态都相同的小图形，每个小图形的线度都是原图形的r倍，通过边长为1/2r的盒子紧密包含A，那么集合A的盒维数为

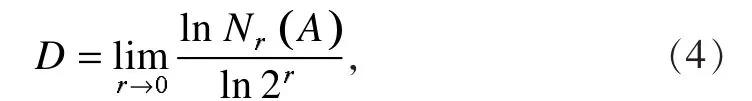
其中Nr（A）为包含集合A所需的最少盒子数。盒维数计算流程如图1所示。

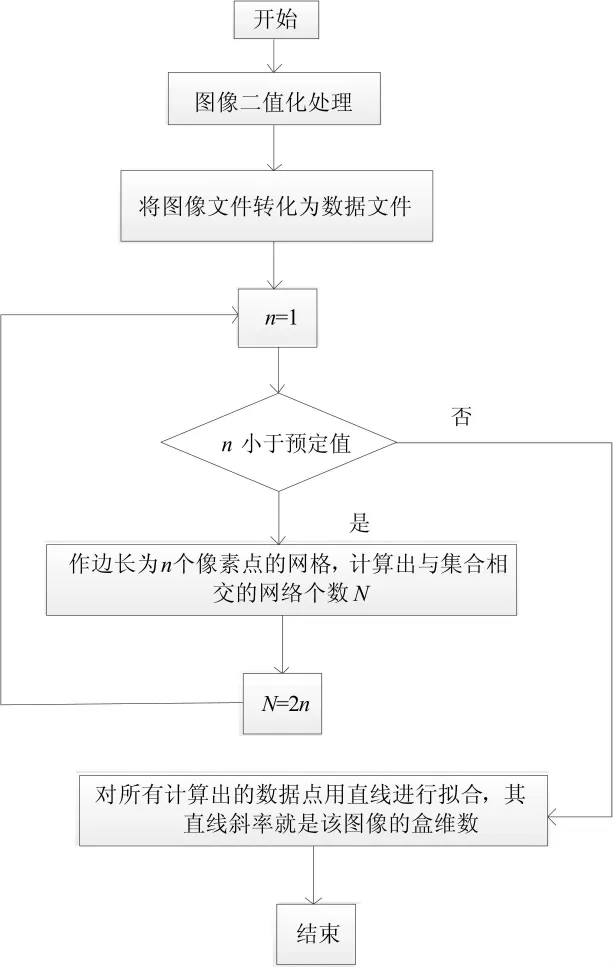
图1　盒维数计算流程图

1.3　图像分形维数的计算

设带有边缘特征的纹理图像Q大小为M×M，由于图像边缘具有不规则性，可以将纹理图像Q理解为三维空间中的曲面。令x，y代表图像Q的平面区间，图像的二维灰度值则用z轴表示，将Q分割为若干个n×n大小的子块（M/2≥n＞1），并把这些网格块理解为 n×n个盒子。假设图像的边缘灰度在第（i，j）个网格中的最大值和最小值不在同一个盒子，而是在第k和第l个盒子中，那么令r=n/M，则完全覆盖第（i，j）个网格需要的盒子数为

覆盖整个纹理图像Q所需要的盒子数为

使用最小二乘法求解式（7），可得出分形维数

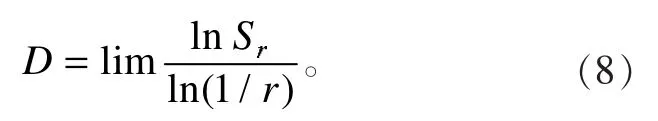
2　图像边缘检测

图像的结构不规则及突变绘出了图像的轮廓，轮廓是进行图像分类的重要依据［6］。轮廓可以定义为局部灰度值发生变化，即两个具有不同灰度值的均匀图像的边界［7］。边缘提取就是将图像灰度值变化大的区域提取出来。经过边缘提取后的图像，数据量大大减少，且保留了图像的特征域和有价值的信息［8］。边缘描述通常包括以下几个特征：边缘强度、边缘方向和边缘位置［9］。

2.1　传统的边缘检测算法

（1）Roberts边缘检测算法

这种方法是利用局部差分算子寻找边缘的算子，采用对角线方向相邻的两像素之差来计算［10］。假设图像 Q 在（i，j）点的像素值为 f（i，j），对图像 Q 进行二维灰度值处理后，（i，j）点的像素值为

选取适当的阈值门限 T，若 R（i，j）≤T，则 R（i，j）属于图像部分；若 R（i，j）＞T，则 R（i，j）为图像的边缘部分［11］。Roberts边缘检测算法虽然定位精度高，但抗噪能力比较弱，且阈值门限T的选取也需要大量的计算［12］。

（2）基于小波的边缘检测

小波理论取自短时傅立叶变换局部化的思想，具体做法是在基于短时傅立叶平移法和伸缩法的前提下，提供一个随频率改变的“时间-频率”窗口，即克服了傅里叶变换窗口大小不随频率变化的缺点［13］。假设函数具有以下特征：

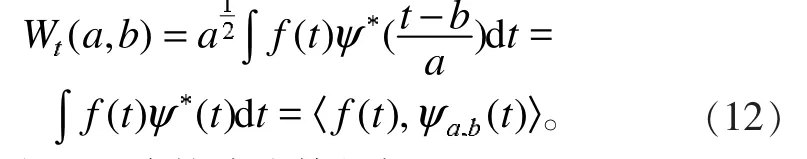
2.2　基于分形理论的边缘特征提取

提取过程是：在传统边缘特征提取算法的基础上，根据分形几何中的压缩映射定理，利用局部迭代函数的收敛性，构造一个迭代函数集［14］，通过对函数集的计算得出边缘特征。由于可以将图像边缘近似地理解为三维空间中的曲面，利用迭代函数集就能够将一幅完整的图像分割成若干个分形结构。

利用分形几何中的压缩映射定理可得到边缘信息，这样虽然可以根据局部迭代函数的收敛性将边缘数据收敛在一起，但在映射变换中，因压缩因子也具有平滑效果，可使边缘部分模糊，而很难找到一个阈值函数进行相应的边缘确认，导致特征提取的准确性不高［15］。为此，可以先找到一个最佳匹配父块，再利用最小二乘法将测量子块与父块进行匹配，得到边缘图像的失真度。失真度越小边缘子块特征越模糊；反之，边缘子块的图像特征越明显。基于分形理论的边缘特征提取算法流程如下：

1）提取Lena图像，设大小为M×N。

2）将Lena图像均匀地分为若干个R子块，每个子块的大小为 2j×2i（i≤M，j≤N），且各个子块没有重叠。

3）在Lena图像中寻找父块，使每个R子块都有与之对应的父块D，将父块D进行压缩映射（包括对父块D进行邻域平均、空间二维变换和灰度变换），通过最小二乘法求出与每一个子块的平方误差最小值d。

4）通过对分形维数的计算选取合适的阈值函数T。

5）比较每一个d与T的大小，得出子块与父块的匹配度。如果d＜T，说明子块与父块的匹配度符合要求，则停止搜索，进行下一子块与父块的匹配搜索；如果d＞T，说明R子块与父块不匹配，则继续搜索并保存R子块的地址信息；如果d=T，则需要根据情况做进一步分析。

6）将与最佳匹配父块D不匹配的子块收集为测度集合，通过零交叉法进一步匹配合适的父块，提取边缘信息，最终得到边缘特征。

3　实验与仿真

利用基于分形理论的图像边缘特征算法，通过MATLAB软件对Lena图像进行边缘提取，同时比较其他几种边缘提取算法的效果，结果如图2所示。由图2可以看出：Roberts边缘检测算法边缘定位不太准确，提取的边缘轮廓相对较粗且和图像信息有较大重合，但是对噪声点图像提取效果较好；基于小波的边缘提取算法边缘提取较为清晰，但是小波基的计算较为麻烦；基于分形理论的边缘特征提取对Lena图像边缘的提取较为准确。

为了验证算法的抗噪性能，对Lena图像添加不同程度的随机噪声（随机噪声系数分别为0.2、0.3、0.4），分别采用基于分形理论和传统的Roberts边缘检测、小波检测算法对加噪图像进行边缘检测。结果如表1所示。

由表1可知：1）随着随机噪声系数的增加，边缘特征提取的错检率在不断增大，而漏检率没有发生改变，这说明随机噪声对各种算法的漏检率影响不大；2）在随机噪声存在的情况下，本文算法错检率明显小于其他算法，具有一定的鲁棒性。

图2　Lena图像边缘提取效果对比

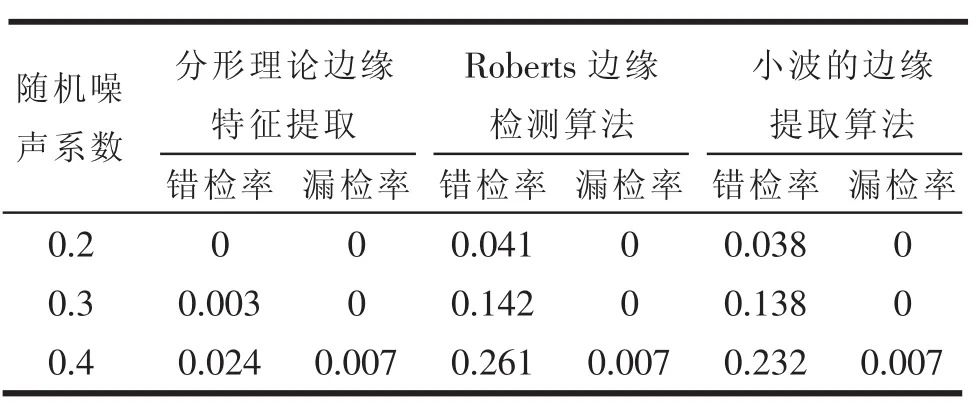
表1　不同算法对加噪图像边缘检测结果

4　结束语

我们在传统图像边缘提取算法的基础上，利用分形检测对噪声不敏感的特点，对传统边缘提取算法进行改进，通过实验证明了该算法的有效性和抗噪性相比传统算法有了极大提高。不过，基于分形理论的边缘提取算法过于依赖阈值T的选取，而阈值T决定着子块与最佳匹配父块的匹配程度，也就是边缘提取的准确性，因此我们下一步要做的研究是从全局和局部两个方向描述边缘图像的分形维数，将对R子块与最佳匹配父块D不匹配的数据信息进行局部匹配，从而减少计算时间，得到更精确的图像边缘分割效果。