解 选择题的技巧
文 /张建芳

解数学选择题,需要根据题目的不同特点,灵活选用解法,才能简捷求解.解选择题的常用方法有下面几种.
一、直接法
从题目的条件出发,利用定义、定理、性质、公式等知识,通过运算或推理,直接求得结论,从而确定正确选项.

二、排除法
通过推理,排除不正确选项后,剩下唯一的选项就是正确的选项.如果不能立即得到正确的选项,至少可以缩小选择范围,提高解题的准确率.
例2在同一平面直角坐标系中,函数y=mx+m(m≠0)与的图象可能是()

解:选项A,由反比例函数图象得m<0,则直线经过第二、三、四象限,A错误;
选项B,由反比例函数图象得m>0,则直线经过第一、二、三象限,B错误;
选项C,由反比例函数图象得m<0,则直线经过第二、三、四象限,C错误;
选项D,由反比例函数图象得m>0,则直线经过第一、二、三象限,D正确.
选D.
温馨小提示:利用反比例函数图象确定m的符号,再根据m的符号对一次函数图象的位置进行判断,从而判断该选项是否正确.
三、验证法

图1
将四个选项分别代入题设中检验,从而确定答案.
例3 如图1,已知MB=ND,∠MBA=∠NDC,下列哪个条件不能判定△ABM≌△CDN()

解:选项A,加上∠M=∠N可证明△ABM≌△CDN,不合题意;
选项B,加上AB=CD可证明△ABM≌△CDN,不合题意;
选项C,加上AM∥CN可得∠A=∠NCD,可证明△ABM≌△CDN,不合题意;
选项D,加上AM=CN不能证明△ABM≌△CDN,符合题意.
选D.
温馨小提示:验证法的优点是条件一目了然,分析判断有根据,一到两次的验证就能得到正确答案,方法简单易学,准确率高;缺点是若分析判断不准确,就需要验证三次,计算量大.
四、特殊值法

∴y2<y1<y3.选B.
温馨小提示:取特殊值解题时,所选的值要符合条件,且易于计算.
五、归纳猜想法
对于数字或规律探索问题,可用归纳猜想法求解.
例 5 如图2,在平面直角坐标系中,A(0,0),B(2,0),△AP1B是等腰直角三角形,且∠P1=90°,把△AP1B绕点B顺时针旋转180°,得到△BP2C;把△BP2C绕点C顺时针旋转180°,得到△CP3D.依此类推,则旋转第2018次后,得到的等腰直角三角形的直角顶点P2019的坐标为()

解:∵A(0,0),B(2,0),△AP1B是等腰直角三角形,且∠P1=90°,∴P1(1,1).
∵把△AP1B绕点B顺时针旋转180°,得到△BP2C1,∴P2(3,-1).
同理可得P3(5,1),P4(7,-1),P5(9,1),…,
∴P2n+1(4n+1,1),P2n+2(4n+3,-1)(n为自然数).
∵2019=2×1009+1,∴P2019(4037,1).选C.
温馨小提示:本题考查了图形的旋转,利用对称知识找出点的坐标变化规律.

图2
六、数形结合法
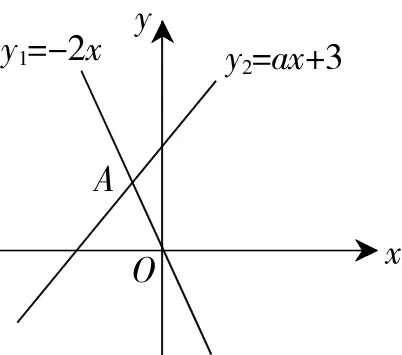
图3
例6 如图3,函数y1=-2x与y2=ax+3的图象相交于点A(m,2),则关于x的不等式-2x>ax+3的解集是()

解:∵直线y1=-2x过点A(m,2),∴-2m=2,解得m=-1,
∴A(-1,2),
由图象可得,当x<-1时,直线y1=-2x在直线y2=ax+3的上方,
∴不等式-2x>ax+3的解集为x<-1.选D.
温馨小提示:求出交点A的坐标,根据函数图象的位置关系确定不等式的解集.
七、估算法
例7如图4,正方形ABCD的边长为9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH.若BE∶EC=2∶1,则线段CH的长是()


图4
在Rt△CEH中,由于EH是斜边,所以EH>CH,又EH=DH,而DH+CH=9cm,可知CH<4.5,所以只有选项A和B符合.若CH=3,则EH=DH=6,而3,3,6不构成三角形,舍去. 选B.
温馨小提示:估算不追求计算的精确,而追求方法的正确.

