生活中的函数问题
文 /谢小芳
函数是初中数学的重要内容.我们主要学习了一次函数、反比例函数和二次函数,它们在生活中的应用非常广泛,请看下面的例子.
一、生活中的函数模型
例1如图1,一种斜挎包的挎带由双层部分、单层部分和调节扣构成.小敏用后发现,通过调节扣加长或缩短单层部分的长度,可以使挎带的长度(单层部分与双层部分长度的和,其中调节扣所占的长度忽略不计)加长或缩短.设单层部分的长度为xcm,双层部分的长度为ycm,经测量,得到如下数据:

图1

单层部分的长度x(cm)双层部分的长度y(cm)……4 6 8 150 73 72 71 10 ……
(1)根据表中数据的规律,填写表格,并直接写出y关于x的函数解析式;
(2)根据小敏的身高和习惯,挎带的长度为120cm时,背起来正合适,请求出此时单层部分的长度;
(3)设挎带的长度为lcm,求l的取值范围.
解:(1)在表格两空中,分别填70,0.
由表格可知,y是x的一次函数,设y=kx+b.

∴单层部分的长度为90cm.
∴75≤l≤150.
点评:没有明确函数类型,需要探索表格数据呈现的规律,根据三类函数的特性,确定函数类别,用待定系数法求解析式.
二、生活中的函数最值
例2某蓝莓种植生产基地产销两旺,采摘的蓝莓部分加工销售,部分直接销售,且当天都能销售完,直接销售是40元/斤,加工销售是130元/斤(不计损耗).已知基地雇佣20名工人,每名工人只能参与采摘和加工中的一项工作,每人每天可以采摘70斤或加工35斤.设安排x名工人采摘蓝莓,剩下的工人加工蓝莓.
(1)若基地一天的总销售收入为y元,求y与x的函数关系式;
(2)如何分配工人,才能使一天的销售收入最大,并求出最大值.
解:(1)y=[70x-(20-x)×35]×40+(20-x)×35×130=-350x+63 000.
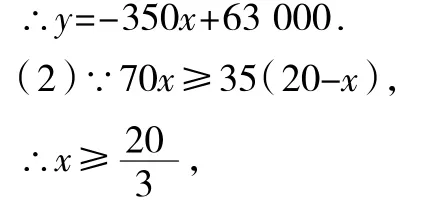
∵x为正整数,且x≤20,
∴7≤x≤20,
在y=-350x+63 000中,k=-350<0,
∴y随x增大而减小,
当x=7时,y取最大值,最大值为-350×7+63 000=60 550.
答:安排7名工人采摘蓝莓,13名工人加工蓝莓,才能使一天的收入最大,最大收入为60 550元.
点评:求一次函数最值的步骤:求出一次函数解析式;确定自变量的取值范围;根据函数的增减性确定最值.
例3某农场拟建一间矩形种牛饲养室.饲养室的一面靠墙(墙足够长),已知建筑材料可建围墙的总长为50m.设饲养室长为x(m),占地面积为y(m2).
(1)如图2,问饲养室长x为多少时,占地面积y最大?
(2)如图3,现要求在图中所示位置留2m宽的门,且仍使饲养室的占地面积最大.小敏说:“只要饲养室长比(1)中的长多2m就行了.”请你通过计算,判断小敏的说法是否正确.

图2
∴当x=25时,占地面积最大,
即饲养室长x为25m时,占地面积y最大.

∴当x=26时,占地面积最大,
即饲养室长x为26m时,占地面积y最大.
∵26-25=1≠2,
∴小敏的说法不正确.
点评:列出二次函数的表达式,将其配成顶点式,根据自变量的取值范围确定最值.
三、生活中的函数图象
例4某市规定每月用水18立方米以内(含18立方米)和用水18立方米以上两种不同的收费标准.某用户每月应交水费y(元)是用水量x(立方米)的函数,其图象如图4所示.
(1)若某用户某月用水量为18立方米,则应交水费多少元?
(2)当x>18时,求y关于x的函数表达式,若小敏家某月交水费81元,则这个月用水量为多少立方米?
解:(1)由图4可知,月用水量18立方米,交水费45元.
(2)由81元>45元,所以用水量超过18立方米,
设y=kx+b(x≥18),
∵ 直线经过点(18,45),(28,75),


图4
∴y关于x的函数解析式为y=3x-9(x≥18),
当y=81时,3x-9=81,解得x=30.
答:这个月用水量为30立方米.
点评:本题的函数图象是以分段方式呈现的,称作分段函数.解这类问题,要注意几个方面:(1)寻找函数的分段点;(2)对每一段函数关系,求出解析式;(3)利用解析式解决相关问题.
四、生活中的函数说理
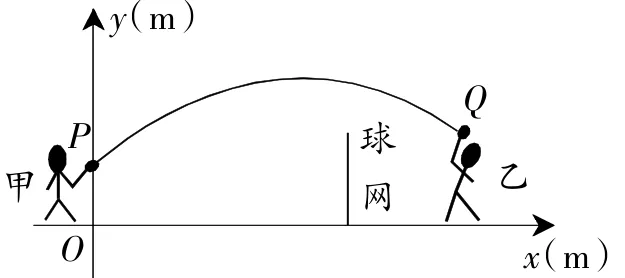
图5
例5甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图5,甲在O点正上方1m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式y=a(x-4)2+h,已知点O与球网的水平距离为5m,球网的高度为1.55m.
(2)若甲发球过网后,羽毛球飞行到与点O的水平距离为7m,离地面的高度为的Q处时,乙扣球成功,求a的值.
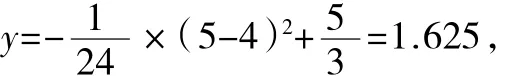
∵1.625>1.55,
∴此球能过网.

点评:利用二次函数解决抛物线型的球类运动、隧道、大桥和拱门等实际问题时,要恰当地建立平面直角坐标系,把这些实际问题中的数据转化为抛物线上的点,从而确定抛物线的解析式,利用解析式去解决问题,或进行判断说理.

