函数易错题分析
文 /李苏娟
在解决有关函数问题时,容易出现错误,现举例加以分析,希望你能从中吸取教训,避免犯类似的错误.
一、没有掌握对称点的坐标特征
例1在平面直角坐标系中,点A与点B关于y轴对称,点A的坐标是(2,-8),则点B的坐标是()

错解:B.
剖析:点A(2,-8)关于y轴对称点的坐标是(-2,-8). 选A.
温馨小提示:点(x,y)关于x轴的对称点是(x,-y),关于y轴的对称点是(-x,y),关于原点的对称点是(-x,-y).
二、忽视实际意义
例2下列图象中,能反映等腰三角形顶角y(度)与底角x(度)之间的函数关系的是()
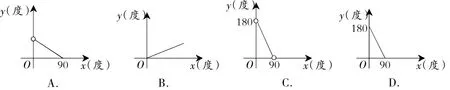
错解:选D.
剖析:等腰三角形的两个底角相等,所以x+x+y=180,即y=180-2x.
由y>0得x<90,又x>0,∴0<x<90. 选C.
温馨小提示:在实际问题中,自变量的取值范围会受到限制,对应的函数图象可能是原函数图象的一部分.
三、求自变量取值范围时考虑问题不全面
错解:因x-1≥0,∴x≥1.
剖析:没有考虑分母不等于0.因此,x的取值范围是x≥1且x≠2.
温馨小提示:根据自变量所在的位置确定其取值范围,最后取公共部分.
四、图象选择错误
例4小明从家到学校,先匀速步行到车站,等了几分钟后坐上了公交车.公交车沿着公路匀速行驶一段时间后到达学校.小明从家到学校的路程s(m)与时间t(min)的大致图象是()
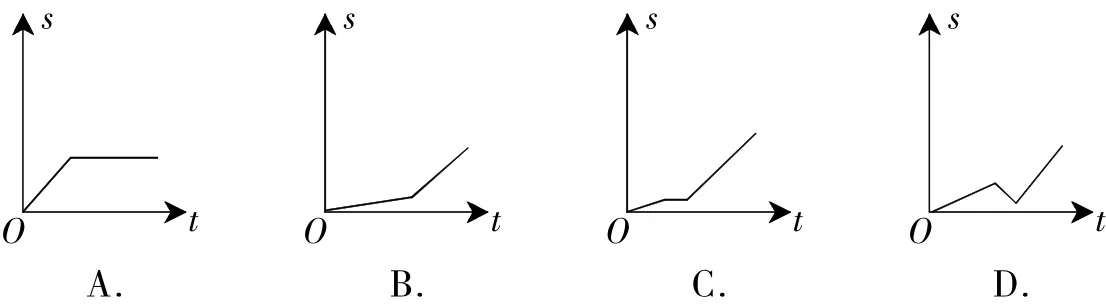
错解:选D.
剖析:在车站等车的几分钟,这段时间小明与家之间的距离s没有变化,图象为平行于t轴的线段;公交车的速度比步行的速度快,对应线段的倾斜程度变“陡”.选C.
温馨小提示:这类题主要考查对图象的理解能力,是中考命题的热点,有一定的难度.函数的表示方法除了图象法外,还有列表法和解析式法.
五、利用反比例函数的性质时不分象限
例 5 若点A(-1,y1),B(1,y2),C(3,y3)在反比例函数的图象上,则y1,y2,y3的大小关系是()

错解:∵k=-3<0,由反比例函数的性质可知,y随x的增大而增大,
而-1<1<3,∴y1<y2<y3. 选A.
剖析:反比例函数图象的性质是分象限研究的,当k<0时,图象在第二、四象限,在每个象限内,y随x的增大而增大.
由x>0可知,当x2<x3时,y2<y3;由y2,y3都小于0,而y1大于0,有y2<y3<y1. 选B.
温馨小提示:反比例函数图象的性质适合于同一个象限.本题可求出y1,y2,y3的值,它们的值分别为3,-3,-1,所以y2<y3<y1.还可以画出反比例函数的图象,借助于图象可得y2<y3<y1.
六、没有掌握图象平移的规律
例6将抛物线y=2x2向右平移3个单位,再向下平移5个单位,得到的抛物线的表达式为()

错解:选D.
剖析:抛物线的平移就是顶点的平移.抛物线y=2x2向右平移3个单位为y=2(x-3)2,再向下平移5个单位,抛物线的表达式为y=2(x-3)2-5.选A.
温馨小提示:二次函数图象的平移,实质上是顶点坐标的平移,只要确定平移前后的顶点坐标,就可以写出平移后的解析式.
七、忽视坐标与长度的关系
例 7 如图1,抛物线y=ax2+bx+c交x轴于A(-2,0)和点B,交y轴的负半轴于点C,且OB=OC.下列结论:①2b-c=2;②;③ac=b-1;其中正确的结论有()
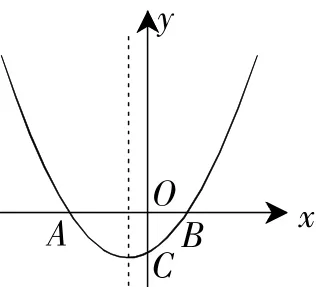
图1

错解:选A.
正解:当x=0时,y=ax2+bx+c=c.∴C(0,c).∵c<0,∴OC=-c.
∵OB=OC,∴B(-c,0).
∵A(-2,0),∴-c,-2是ax2+bx+c=0的两个不相等的实数根,,②正确;是方程的两个不相等的实数根,
∴-c+(-2)=-2b,即2b-c=2,①正确;
把B(-c,0)代入y=ax2+bx+c,得0=a(-c)2+b·(-c)+c,即ac2-bc+c=0,
∵c≠0,∴ac-b+1=0,∴ac=b-1,③正确;
选D.
温馨小提示:在解决函数问题时,要注意线段长度与坐标的转化关系,即由点的坐标求线段长需要取绝对值,由线段长求点的坐标要加上点所在象限的符号.

