基于ANSYS Workbench的细纱机机架动态仿真分析

李京 范真 陈祖英 张伟 徐旭松

摘 要：机架部件的稳定性是成纱质量的关键因素。通过ANSYS Workbench对细纱机机架进行模态分析和随机振动分析，得到机架的前8阶的振型以及随机振动位移响应值，并根据分析结果对机架部件作了适当改进并进行仿真分析。结果表明：机架的前3阶固有频率分别提高了27.7%、47.9%、23.6%；机架X、Y、Z方向瞬间增大峰值处的功率密度谱值分别减小了65.9%、41.8%、83.5%。该结果可为细纱机机架的结构优化设计提供参考。

关键词：细纱机机架；固有频率；振型；最大位移；功率谱密度

中图分类号：TH122

文献标志码：A

文章编号：1009-265X（2018）02-0090-07

Dynamic Simulation Analysis of Spinning FrameRack Based on ANSYS Workbench

LI Jing1， FAN Zhen1， CHEN Zuying2， ZHANG Wei1， XU Xusong1

（1.School of Mechanical Engineering， Jiangsu University of Technology， Changzhou 213001， China；2.Textile Machinery Manufacture Co.， Ltd， Changzhou 213001， China）

Abstract：The stability of rack component is a key factor of the quality of yarn. Modal analysis and random vibration analysis of spinning frame rack were carried out with the help of ANSYS Workbench. First eight bands of vibration form and random vibration displacement response values were gained. According to the analysis results， the improvement of spinning frame rack was implemented and its simulation analysis was conducted， too. The analysis results show that first three natural frequencies of the rack increase by 27.7%， 47.9% and 23.6% respectively， and the PSD values at the point of increasing peak quickly along the direction of X， Y， Z decrease by 65.9%， 41.8% and 83.5% respectively. The results provide a reference for the optimal design of spinning frame rack.

Key words：spinning frame rack； natural frequency； vibration form； maximum displacement； PSD

機架作为细纱机的支撑部件，在工作过程中需要承受很多复杂多变力的作用，易出现共振现象，使得中墙板侧向、机梁、龙筋等扭曲变形；由于工况复杂多变，细纱机机架在工作时还会出现随机振动，这会严重影响纺纱质量，降低生产效率。所以有必要对机架部件进行模态分析以及随机振动分析。

张元通[1]通过ANSYS Workbench对颗粒机机架进行模态分析，为颗粒机进一步仿真分析打下了基础；孙康等[2]对刮板式花生脱壳机机架进行仿真分析，验证了脱壳机的工作频率和皮带传动引起的振动频率都远小于其第一阶固有频率，不会发生共振现象；韦辽等[3]对CA6140机床主轴箱进行模态和随机振动分析，判断机构设计的合理性。以上研究仅进行了仿真分析，没有给出具体的改进方案。

本文以TH588型细纱机机架为研究对象，利用有限元仿真软件ANSYS Workbench进行模态分析和随机振动仿真分析；在此基础上对振动最大处给出了改进方案，并对改进结构的合理性进行验证，为后续细纱机机架的优化设计提供参考依据。

1 理论基础

模态分析主要研究结构的振动特性，即结构的固有频率及振型。模态分析作为基本的动力学分析，是其他动力学分析的基础，如随机振动分析、谐响应分析、响应谱分析等都在模态分析的基础上进行[4]。

对于一个N自由度的机械系统，其结构自由度的常数微分方程为[5]：

[M]{x″}+[C]{x′}+[K]{x}={F（t）}（1）

式中：[M]是质量矩阵；[C]是阻尼矩阵；[K]是刚度矩阵；{x}是位移矢量；{x′}是速度矢量；{x″}是加速度矢量。

随机振动分析是一种基于概率统计学理论的谱分析技术，也被称为功率密度分析。功率谱密度函数（PSD）是随机变量自相关函数的频域描述，能够反映随机载荷的频率成分[6]。

细纱机在工作过程中，由于外界振动载荷的激励，导致细纱机工作系统产生复杂多变的振动现象，所以有必要对机架进行随机振动分析。

2 有限元模型构建

2.1 实体模型构建

TH588型细纱机机架结构简图如图1所示，主要由中墙板、龙筋、机梁通过螺栓连接固结为一个整体。在三维建模过程中对机架进行了适当的简化，忽略了对机架有限元分析影响较小的特征，如一些圆角、倒角、小孔等。

2.2 网格划分

运用三维建模软件建立机架的实体模型后，按照Parasolid标准[7]，将机架以“.x_t”格式输出，然后导入到Workbench后，设置单元大小为20 mm，进行网格划分。机架网格划分结果如图2所示。

2.3 材料属性和边界条件

机架材料为HT200，弹性模量2.06×1011 Pa，泊松比0.3，质量密度7.2×103 kg/m3，弯曲强度400 MPa。机架通过地脚螺栓连接使机架固定在水平地面，在模态分析时，把机架4个底座施加固定约束。

3 模态分析

模态分析的优点就在于可以使结构设计避免发生共振现象，或使结构以预定的频率进行振动[4]。通过模态分析可以判断细纱机机架在设计过程中是否存在薄弱环节，由此可以对薄弱环节进行相应改进。

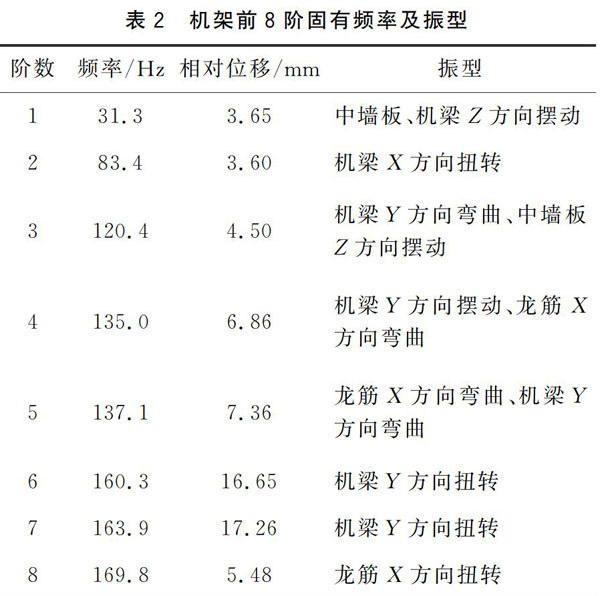
因为机构的前几阶模态对结构影响较大[8]，经过模态分析后，机架前8阶振型如图3所示，固有频率及振型如表2所示。

由图3及表2可以看出，机架的1阶固有频率为31.3 Hz，大于主轴转速（1 300 r/min=21.7 Hz），与主轴不会发生共振现象。机架前8阶振型中相对位移最大的位置发生在第7阶模态的机梁部位，最大位移为17.3 Hz，此时机架的固有频率为163.9 Hz。由表2还可以得出，机架机梁部位反复出现摆动、弯曲、扭转等变形，这使得机架在工作过程中直接影响纺纱质量。

4 随机振动分析

随机振动分析在模态分析的基础上进一步求解得到。计算得到的机架X、Y、Z方向的1σ位移响应云图如图4所示。

由图4可以看出，机架水平Z方向的振动最大，最大值同样出现在机架机梁中部。所以可以选择机架一侧机梁中点为研究对象。提取各向位移PSD谱曲线图及瞬间增大的峰值处的位移响应功率密度谱值，如图5及表3所示。

功率谱密度是结构在随机载荷激励下响应的统计结果，反映了功率谱密度与频率的关系。从图5及表3可以看出：在134.9Hz时出现了瞬间增大的峰值，此时的位移响应功率密度谱值为7.077×10-3 mm2/Hz，瞬间增大峰值对应了模态分析中的第4阶固有频率下振幅的最大变化量；在163.9Hz时出现了瞬间增大的峰值，此时的位移响应功率密度谱值为8.708×10-3 mm2/Hz，瞬间增大峰值对应了模态分析中的第7阶固有频率下振幅的最大变化量；在31.3Hz时出现了瞬间增大的峰值，此时的位移响应功率密度谱值为3.031 mm2/Hz，瞬间增大峰值对应了模态分析中的第1阶固有频率下振幅的最大变化量。结合模态分析和随机振动分析可以得出，机架结构在第1、4、7阶频率下的参振系数较高，同样也说明了机架机梁最先发生疲劳破坏，所以在以后的改进设计中把机梁作为重点设计对象。

5 机架改进及分析

5.1 机架结构的改进

结合以上机架模态和随机振动分析的结果对其进行结构改进，从图6原机架应力响应云图可以看出，机架整体等效应力分布比较均匀。只是机梁处的变形最大且变形频繁，最先出现疲劳变形，所以在机梁处添加三根横拉杆[9-10]，添加位置如图7所示。

5.2 模态分析对比

对添加横拉杆后的机架结构进行模态分析，提取改进后机架的前8阶振型如图8所示。

由图8可以看出：改进后机架的前8阶固有频率都有所提高，前3阶固有频率为39.95、123.37、148.89Hz，与改进前机架的前3阶固有频率相比，分别提高了27.7%、47.9%、23.6%。从模态分析的对比结果可以看出，改进机架结构的固有频率有所提高，进一步减小了共振现象发生的概率，所以，机架的改进方案可行。

5.3 随机振动分析对比

在模态分析的基础上，对改进后的机架进行随机振动分析，提取机架X、Y、Z方向的1σ位移响应云图如图9所示。

由随机振动分析可以得出，改进后机架的X、Y、Z方向的响应最大位移分别为0.191 3、0.243 7、0.830 3，与改进之前相比分别减小了41.9%、21.6%、29.4%。

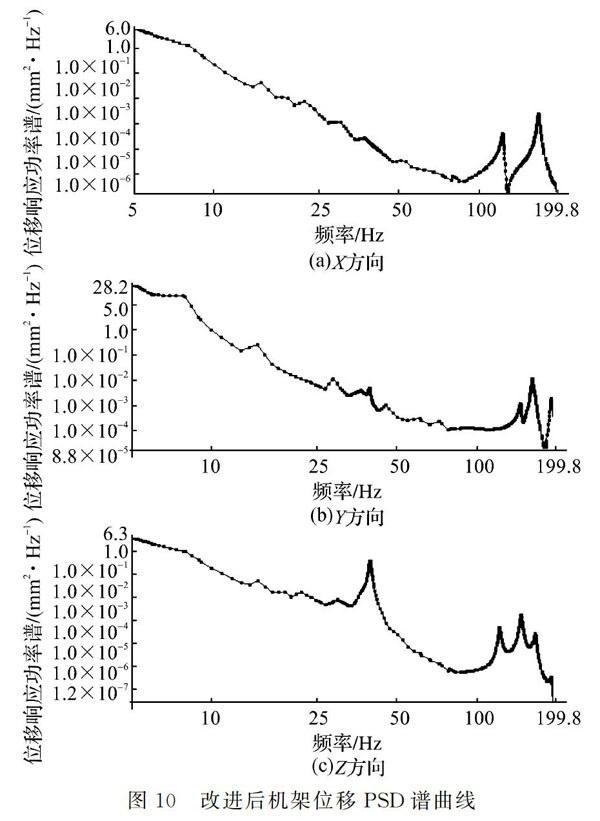
同样选取机架一侧机梁中点为研究对象，X、Y、Z方向瞬间峰值处的频率以及位移响应功率密度谱值如图10所示。

从图10可以得出，改进后机架X、Y、Z方向瞬间增大峰值处位移响应功率密度谱值分别为2.411×10-3、5.035 9×10-3、0.499 63 mm2/Hz，与改进前相比分别减小了65.9%、41.8%、83.5%。

6 结 论

a）利用有限元软件ANSYS Workbench对细纱机机架进行模态分析得出其前8阶固有频率，判断出机架结构不会与主轴系统发生共振现象，并且相对位移最大的位置发生在第七阶模态的机梁部位。

b）在模态分析的基础上对机架进行随机振动分析，得到机架X、Y、Z方向的1σ位移响应云图，从图中同样可以看出机架的最大位移发生在机梁部位；以机梁中部一节点为研究对象，得到其X、Y、Z方向位移PSD谱曲线及相应的瞬间增大峰值处的位移响应功率密度谱值，X、Y、Z方向位移PSD谱曲线瞬间增大峰值分别对应模态分析的第4、7、1阶频率下振幅的最大变化量。

c）根据机架模態和随机振动分析结果，对机架结构进行改进，在两根机梁上添加3根横拉杆；对改进后的机架进行模态和随机振动分析，结果表明，改进后机架的前3阶固有频率分别提高了27.7%、47.9%、23.6%；机架X、Y、Z方向瞬间增大峰值处位移响应功率密度谱值分别为2.411×10-3、5.036×10-3、0.499 6 mm2/Hz，与改进前相比分别减小了65.9%、41.8%、83.5%。

参考文献：

[1] 张元通.基于ANSYS Workbench的颗粒机机架的模态分析[J].机械设计与制造，2011，40（2）：110-112.

[2] 孙康，王军峰.刮板式花生脱壳机机架的模态分析[J].农业化研究，2013（6）：66-69.

[3] 韦辽，李健.CA6140机床主轴箱模态和随机振动分析[J].农业装备与车辆工程，2013，51（10）：49-51.

[4] 陆爽，孙明礼，丁金福，等.ANSYS Workbench13.0有限元分析从入门到精通[M].北京：机械工业出版社，2012：186-187.

[5] 郑文鑫，方文熙，张德晖，等.基于CATIA的烟秆清理机机架模态分析[J].福建农机，2014（1）：29-31.

[6] 熊兴荣，王正浩，沈磊.擦窗机吊臂伸展机构模态和随机振动分析[J].建筑机械，2015（7）：81-85.

[7] 刘丹萍，蒋占四，冯建国，等.机床主轴的SolidWorks建模与有限元分析[J].机床与液压，2013，41（21）：123-125.

[8] 夏敏敏，李立军，詹春生.基于ANSYS的插齿机液体静压轴承模态分析[J].机械研究与应用，2010，23（1）：94-95.

[9] 胡世军，梁东旭，张代录，等.基于ANSYS的主轴箱体模态分析及拓扑优化[J].机械制造，2012，50（11）：6-9.

[10] 刘选伟，金亮，王景立.基于ANSYS Workbench的深松机机架模态分析[J].农机化研究，2015（5）：29-31.