模态分析在浮置板轨道参数优化中的应用

李贵阔　刘帅

摘 要：以浮置板轨道为研究对象，建立有限元模型，对不同厚度、宽度下的浮置板轨道进行了模态分析。

关键词：模态分析；浮置板轨道；振动特性；固有频率

中图分类号：U211.3 文献标识码：A DOI：10.15913/j.cnki.kjycx.2015.17.074

浮置板轨道的减振性能与固有频率密切相关，因此，研究浮置板轨道的振动特性是很有必要的。本文采用ANSYS软件中的缩减法，依据模态分析理论，建立浮置板轨道有限元实体模型，计算、分析了参数变化对系统振动频率的影响。

1 浮置板轨道结构参数

钢轨采用60 kg/m的钢轨，钢轨容重为7 960 kN/m3，泊松比为0.3，弹性模量E为210 GPa。浮置板的长度为24 m，宽3 m，高0.5 m，密度为2 500 kg/m3，泊松比为0.2，弹性模量E为32 GPa。扣件的布置间距为0.6 m，刚度为50 kN/mm，阻尼为50 kN·s/m；钢弹簧刚度为10 kN/mm，阻尼为75 kN·s/m。

2 浮置板轨道模型的建立

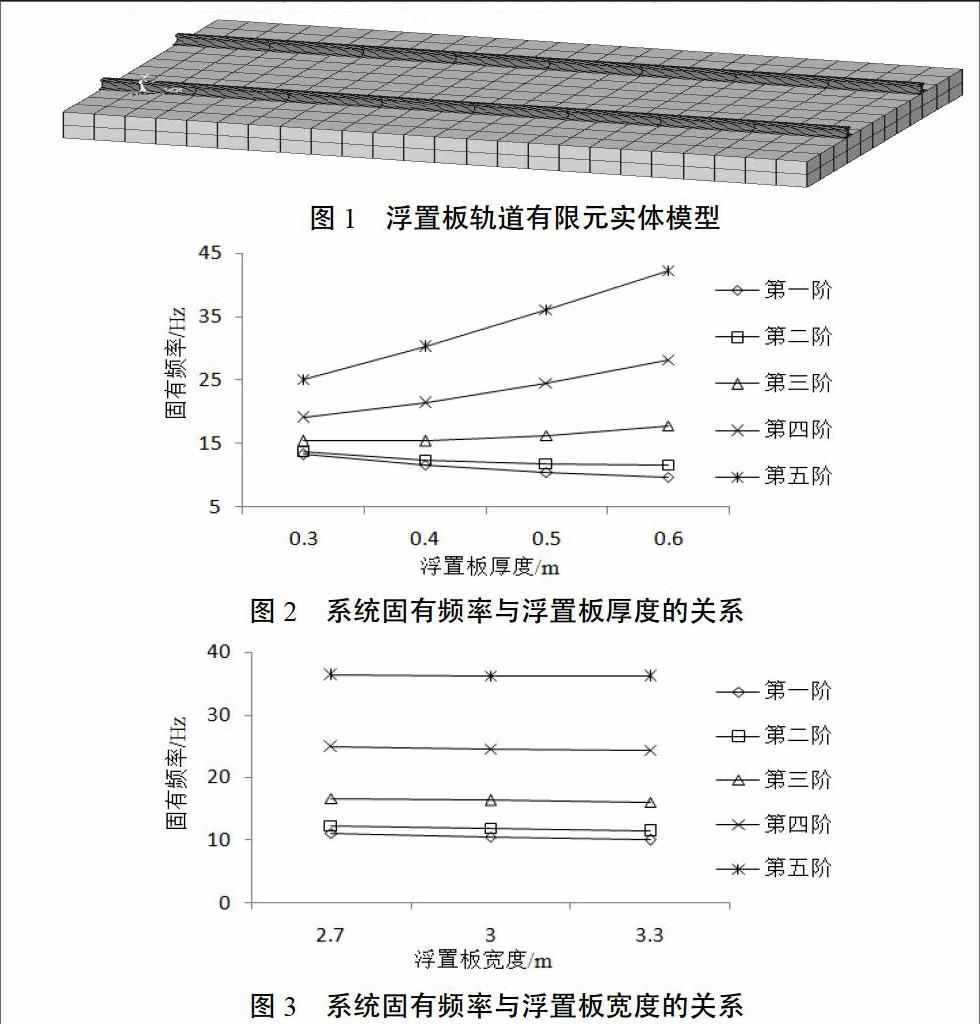
为了准确反映结构的特征和受力特性，运用ANSYS软件建立浮置板轨道结构的三维有限元模型。在有限元模型中，采用BEAM188单元模拟钢轨，扣件和钢弹簧支座用弹簧阻尼单元COMBIN14模拟，浮置板用实体单元SOLID45单元模拟。建立的有限元实体模型如图1所示。

3 模态计算和结果分析

模态分析用于得到结构的固有频率和振型，二者是浮置板轨道结构重要的动力参数。运用模态分析的方法可以在设计阶段分析结构的动力特性，优化结构参数的选择。浮置板轨道结构拥有许多高阶振动模态，在列车经过时，影响隔振效果的主要因素是浮置板轨道结构的固有振动频率，特别是低阶固有频率。在计算时，取前五阶模态进行分析。本文采用的缩减法需要预先定义主自由度，而主自由度的选择对结果有很大的影响。

为了研究轨道结构的振动特性，可从改变系统的参振质量入手，改变浮置板厚度可以使系统的参振质量发生变化。另外，几乎没有文献讨论过浮置板宽度对振动特性的影响。因此，本文以这2个参数的变化为前提分析浮置板厚度和宽度改变对系统固有频率的影响，其影响结果如图2、图3所示。

由图2可知，随着浮置板厚度的增加，系统前两阶频率逐渐变小，而后几阶固有频率却呈增大的趋势。浮置板的厚度增加使得参振质量增加，系统的固有频率降低，同时，浮置板抗弯刚度的增加会减缓浮置板和浮置板轨道轨道结构的变形，进

而提高列车运行的平顺性和安全性。

由图3可知，随着浮置板宽度的增加，浮置板轨道结构的前两阶频率变化不大，后几阶频率几乎没有变化，第一阶频率由11.065 Hz降低到了10.06 Hz，系统固有频率降低了9.08%；第五阶频率由36.311 Hz降低到了36.1 Hz，系统固有频率仅降低了0.6%.因此，在研究浮置板轨道的振动特性时，可以不重点考虑浮置板宽度的影响。

4 结束语

增大浮置板的厚度，浮置板的质量增大，系统前两阶固有频率呈降低趋势。在满足建筑限界要求的前提下，可以适当增加浮置板的厚度，以达到更好的减振效果。

浮置板宽度对系统固有频率的影响比较小，所以，可以不作为重点考虑对象，可以结合施工条件、建筑限界、减振需要等因素综合考虑。

参考文献

[1]耿传智，田苗盛，董国宪.浮置板轨道结构的振动频率分析[J].城市轨道交通研究，2007（3）.

[2]代丰，刘亚航，徐金辉，等.减振型板式轨道的模态分析[J].铁道建筑，2011（9）.

〔编辑：白洁〕