广义相对论、引力波的检验和黑洞热力学的谬误及其发展

张一方

(云南大学 物理系，云南 昆明 650091)

0　引　言

2015年是广义相对论基本完成的百年纪念.爱因斯坦说：“广义相对论的主要意义不在于预言了一些微弱的观测效应，而在于其理论基础的简单性.”他认为广义相对论的基本观念在于：1)引力场和度规场是同一的；2)广义相对性是正确的.结合对应原理，局部时空是Lorentz变换时引入光速c；场方程在弱场近似时对应于万有引力定律就引入引力常数G.S.W.Hawking(1942.01.08-2018.03.14)认为广义相对论两个逻辑上互相独立的假定：1)最革命性的假定；引力对于物质场产生的影响可以用弯曲的度规gij描述，这是“等价原理”的数学表述，广义相对论是一种“度规理论”.2)度规gij与时空中物质和能量的分布由场方程联系.广义相对论的基本思想包含：1)时空结构的不均匀性(度规的Riemann性质).2)度规对物质位置与运动的依赖性(形式上表示为度规张量的分量是引力势).本文探讨引力波对广义相对论的各种验证，等价原理及其推广，某些新的引力理论及黑洞热力学的谬误及其发展.

1　引力波对广义相对论的多项检验

最近引力波成为科学发展中一个举世瞩目的焦点.首先，LIGO和Virgo于2015年9月14日和2015年12月26日两次探测到两个黑洞(BBH)合并产生的能量巨大的引力波[1，2].这是意义非常重大的科学进展[3]，由此正如笔者推测的Rainer Weiss，Barry C.Barish和Kip S.Thorne荣获2017年诺贝尔物理学奖.当时笔者预测进一步的研究可能发现引力波和电磁波速度的差别[3，4].令人高兴的是LIGO和Virgo又于2017年8月17日发现双中子星(BNS)并合产生引力波，两个中子星的质量约为2.26和0.86Mo(M⊙太阳质量)，合并后的质量约为2.74Mo.在并合之前100 s它们分离大约400 km.并且国际引力波电磁对应体观测联盟发现仅仅在该引力波事件后的1.7 s探测到被命名为GRB170817A的伽玛射线暴(GRB)的电磁对应体[5].

众所周知，引力波基于广义相对论.但通常的讨论都是完全基于类比电磁波，这种方法在论证引力波的存在时是非常有力的，然而存在巨大的缺陷，并且忽略了引力波和电磁波之间的重大区别.可能因此爱因斯坦、Landau、Fock、Weinberg[6-9]等大科学家讨论的都只是弱引力场.基于广义相对论的爱因斯坦引力场方程的非线性，相应的一般的引力波方程也是非线性的，由此1996年笔者提出引力波应该是非线性波，并且讨论了它的相应的某些新的特性.引力波应该具有某些不同于电磁波的特性，特别是引力波速应该和电磁波速不同，起码引力场中光线偏转而引力波速度不会偏转[10].

广义相对论一般的引力场方程是非线性方程：

(1)

引力波的非线性特性来源于引力场的非线性本质[10-12].强引力场方程必然是非线性方程，只要方程不是最简单的一级近似的线性方程，方程的解，无论是孤子解、瞬子解、或是扭子解、混沌解等都不能是简单的线性波，而是一类非线性波.由此笔者已经定量获得了某些简单的非线性解[10，11].Kramer等已经讨论过爱因斯坦场方程的某些严格解[13].

新观测到的引力波不仅证实了广义相对论，而且必然是非线性波，因为双黑洞的合并[1，2]和双中子星的并合[5]都必然是非线性机制，并且具有巨大能量的引力波一定的脉冲波(孤子)，例如GW150914、151216 BBH和GW170817、170825 BNS等都是离散的.

通常假设引力波的速度也是光速，而笔者提出二者速度应该不同[10，11].2015年9月14日LIGO的两个探测器在7 ms的时间内观测到相同的引力波.进而新引力波GW170817的一个特征是GW170817后1.7 s观测到伽玛射线暴(GRB)[5]，这个数值很小，但明确指出引力波和电磁波的速度是不同的[10]，而且这应该是广义相对论的必然结果.我们计算获得中子星并合因为引力红移和光偏转导致电磁波延迟的总时间是0.1792 s[14].它大约是观测延迟时间1.7 s的1/10.引力波和电磁波经过40百万秒差距(大约1.3亿光年)的巨大距离和许多次的引力红移偏转，二者的差完全可能增加10倍.更一般，对双度规(biometric)或矢量-张量或层级(stratified)理论两种速度不同，而对广义相对论或标量-张量理论两种速度相同[15].引力是张量场，电磁场是矢量场.笔者探索过电磁广义相对论[16，17]，其中电磁场也是张量场.这样引力波可以检验矢量-张量理论和张量-张量理论.进一步，笔者预言如果正负物质湮灭将产生能量巨大的引力波，并且具有非线性波的特性[4].因此引力波天文学将在负物质的检验中发挥重大作用.2018年又是爱因斯坦预言引力波的100周年.

2　等价原理及其推广

萨哈洛夫认为“引力是空间度规弹性学”.A.Shild在20世纪60年代得出结论，引力红移和强等价原理必然意味着时空弯曲.Yilmaz提出引力场作为能量也受引力作用，发生变形.

广义相对论在动力学中是力、场等价

ma=mH，

(2)

即

(惯性质量)×(加速度)=(引力质量)×(引力场强度).

在一定程度上就是力守恒，对应虚功原理.推广到能等价即mv2/2=mV，所以势V=v2/2应该是能量守恒.

但作为广义相对论基本原理之一的等价原理，一直引起某些学者的疑问，并对其适用范围展开讨论.例如，某些科学家认为等价原理具有局域性[7，8].等价原理恒成立[6]，则速度变大伴随惯性质量增大时，引力质量也增大；但通常是引力场中势能为负.二者不一致.后者与能量守恒，内能转化为动能一致；但引力场与减速系等价才符合等价原理.

力的表示发展、演化时，等价原理也发展、演化.质量发展、演化、变化，其他一切物质量及运动量也如此.同时，等价也可以从力发展为能量等的等价.广义相对论也相应发展，作用量的等价原理非常广泛.

变速场=力场，是矢量场；质量=能量，是标量场；量子论中是Eψ=Hψ；更一般是物质量等价于运动量.可能矢量等价原理与标量等价原理不同.推广还可以有张量、旋量等的等价原理.而最普遍的Lorentz协变方程必须是旋量方程[18].最广泛的等价对应于等式.广义等价包括各种场方程.场越广泛，其对应的等价原理、方程也越广泛.即力、场、能等多种物理-数学量等价.

对匀速运动，静止相对，对力等价；但动能不同，所以能不等价.1976年笔者对等价原理的推广指出一个限度，这是等价原理另一方面的局部性.引力、斥力场对应势能；加速、减速系对应动能；两方面等价[19].笔者认为只要推广非惯性系和引力场，等价原理就可以普遍成立，而克服其“局域性”.在讨论了非惯性系中加速场或减速场，及引力场或斥力场的关系后可以得出结论：等价原理在矢量方面等价，但在非矢量方面有所不同.由此提出了泛等价原理和泛广义相对论，特别是电磁广义相对论.并论证了广义相对论的各种实验检验及不足之处[17].最近，吴雪峰等利用引力波信号对爱因斯坦弱等效原理进行了最新的高精度检验[20].

广义的一切势场等价于非惯性系.笔者提出泛广义相对论[16]，其基本原理是泛广义相对性原理(它的数学表示是表述物理定律的方程具有协变性)，由此导致非惯性运动得到Riemann或任意非Euclid几何，爱因斯坦群及de Sitter群.进而结合对应原理导出方程.相对性原理从伽利略到爱因斯坦，是几何学派；此时质量m在引力相互作用中可以消去.从牛顿到量子力学是动力学派，基本量是p=mv.由此讨论了检验电磁广义相对论的某些可能方案[16].

3　某些新的引力理论

虽然广义相对论作为理论物理的光辉典范，其功勋是举世公认的.但也还存在某些不足之处，因此已经尝试过各种发展广义相对论的方法，如自然补充(1921)、仿射场(1923)；统一场(1929)、五维形式场(1931)、五维场(1938)、双矢量场(1944)、非对称场(1948)[6]等.其余的引力理论还有Gupta(1957)、Kibble(1961)、Carmeli(1972)、Salam(1974)等.各种保留的引力理论都是度规理论[21].广义相对论度规张量类似势能，其它理论附加标量、矢量、张量势能.广义相对论的各种发展理论各相应于有所不同的群.H.Yilmaz，C.Alley(1995)修改广义相对论，引力场本身也在引力作用下发生伸缩现象，如此无黑洞，但有奇点.

天文观察表明：1)武仙座DI双星，质量分别为4.5M⊙和5.2M⊙，距离0.2天文单位，周期10.55 d，近日点进动1.05°/百年，理论值4.07°，广义相对论是2.34°.2)鹿豹座AS的双星质量为3.2M⊙和2.5M⊙，距离0.1天文单位，进动15°，理论值44.3°，广义相对论为8.5°/百年.对这些双星广义相对论不符合.约为1/2，2倍.3)但对射电脉冲星PSR1913+16，进动为4.23°，与广义相对论极符合.

对Lanczos引力理论[22，23]，如果一方面保留Riemann几何，另一方面企图对电磁场合理解释就必须回到Rijkm上.爱因斯坦用分解的方法，将Riemann张量定义作形式上的推广得(1).但它不完全确定，因为方程两边的迹恒为0，导致9个关系式.但正是Riemann张量的那些不包含于爱因斯坦引力方程中的分量，给出在广义相对论范围内更深入了解电磁现象和量子力学现象的线索.附加方程*R=常数，

(3)

(4)

联系于广义相对论方程中四元数计算和Dirac方程(电磁和量子理论的基础)的出现.引力、电磁理论统一的推广是所有物理现象被解释为时空世界的几何性质.度规物质张量等于宏观物理事件的物质张量，如Minkowski运动张量或Maxwell的能量-动量张量，或二者的组合.笔者在简介几何动力学后，探讨了相互作用的几何统一，提出了5维时空及其5种具体情况，其中第5维可以是与h相关的微观特性，或与质量m等相关，并联系于SU(5).进一步讨论了高维统一理论，并指出其中柱形卷曲空间的光速是可变的.然后探索了广义相对论和量子论的统一，非欧和非阿几何的统一.对Riemann几何和Lobachevsky几何进行了比较.并且讨论对称、反对称和超对称性及其统一.一般的矩阵及相应的各种理论都可以分解为对称和反对称部分之和，由此联系于超对称性[24].

四维Riemann几何的内禀结构元素φi(矢势)、gij(度规张量)、Hijk(16个分量的自旋张量)、Rijkm(Riemann张量)在广义相对论的范围提供了合理解释电磁和量子现象的所有必要而充分的基本根据.

物质场的自旋对引力场的影响.Cantan，Weyl及Sciama，Kibble把物质自旋和时空挠率结合，修改场方程.平移变换(对称性和几何量)得到时空挠率(几何性质)，联系于爱因斯坦方程变为Cantan方程，自旋流密度(物理性质)导致Lorentz旋转.进一步的发展是有挠有旋时的场及其方程.

有自旋的粒子在引力场中受自旋和时空曲率的附加作用，使运动偏离测地短程线.自旋取向不同，作用有正有负，类似电磁理论.致密天体的自转能吸引附近的空间、时间围绕其一同转动，称为“框架拖曳”.1997年11月麻省理工学院的崔伟和意大利科学家L.斯特拉的两个实验组称已经发现此效应.

Birkhoff引力论

(5)

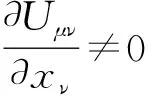
爱因斯坦等的不对称度规场gij是一种新几何、新空间，是Riemann几何的推广，也是宏观场的统一，其基本公式为：

(6)

电磁场导致时空度规gik不对称.Fik完全类似电磁场张量，其空间分量和时空混合张量都反对称；在某些(如Lorentz)条件下可以化为四矢势Ai.

这不是一般广义相对论的Riemann几何，Riemann几何要求gik对易.gik不对易则是推广的Riemann几何，或是具有某些特性(挠率)的Riemann几何.这导致Γl，ik对i，k不对称(表示挠率)，不对称场即挠率场，其中电磁场产生挠率.gij不对易几何上表示最普遍的度规.

gik不对易，联系于不对易的量子力学.电磁场导致与乘积顺序有关.电磁场Ai化为张量形式gik都不对称.只有对易就是引力场.只有反对易是电磁场，运动方程此时化为Lorentz力.两种场都有就是组合场，或不对称场.这是引力场、电磁场的一种统一.

对电磁场，如果1)Γ～(对应)A，则R～F；要求Flm反对称，则只能是Rlm=0[25，26].2)Aν～gμν，则

2Γα，μν-gνα，μ=gμα，ν-gμν，α=Fμνα，

(7)

Fμνα，α=(2Γα，μν)，α-gνα，μα.

(8)

引入类Lorentz条件gνα，α=0，则

Fμνα，α=(2Γα，μν)，α=(4π/c)jμν.

(9)

此时电荷导致时空是Riemann几何.只要下标ij对称就有ijk轮换的Bianchi恒等式或第一组Maxwell方程.

笔者提出了高维时空中一般的引力-电磁统一的非对称度规场的数学形式[26]，其最一般的公式假设为：

Uμν=Rμν+Fμν.

(10)

引力相互作用具有爱因斯坦坐标广义协变的GL(4，R)对称性和Weyl规范不变的SL(2，C)对称性[27，28].因此各种包含广义相对论的引力场理论，其群也应该包含SL(2，C).

4　黑洞热力学的谬误及其发展

毫无疑问，熵是科学的一个伟大发展，也是人类对自身及其环境深刻认识的结果.它对我们冷静客观地理解自然界具有极大的意义，并且已经被广泛应用于许多方面，甚至成为哲学家热烈讨论的话题.热力学第二定律指出在孤立系统中熵永远增加，并趋于无序.一个特例是著名的Boltzmann公式S=lnW，其中W是一个宏观态的等几率微观态的数.

但是，热力学第二定律似乎也被某些人提到了一个神秘崇高的地位，甚至被任意推广而成为一种信仰.伟大的天文学家爱丁顿就认为：“熵永远增加的定律在自然定律中占有至高无上的地位.”里夫金等更提出熵是一种新的支配一切的世界观[29].然而热力学第二定律作为一种科学，我们有必要对它进行一些新的探讨.笔者论证负温度就是由信仰导致的谬误：在重述负温度以后发现它与通常温度的意义及物理和数学的某些基本概念是完全矛盾的.负温度必然导致熵减，它是基于Kelvin温标及条件dU>0和dS<0.反之，dU<0和dS>0时也是负温度[30，31].

黑洞是广义相对论的一个重要结果.而黑洞热力学最早起源于方程的类似性[32]和Hawking的面积增加定理：黑洞的视界面积永不减少[33]，这类似孤立系统的熵增.实际上，这只是黑洞演化方向的必然条件，与热力学和统计力学无关.但是，Bekenstein(1947.5.1-2015.8.16)相信热力学第二定律[34-36]，并坚持这种类似性作为黑洞热力学方案的基础，黑洞的熵就是它的面积，由此几何概念生发出许多物理推论.黑洞将得到熵增，并且获得巨大的Bekenstein数101079.

Bekenstein提出广义的热力学第二定律[34-36]：黑洞外一般熵的和S0和总的黑洞熵绝不减少，并在黑洞一般的转化结果中增加.这是一个方程：

ΔS0+ΔSBH≥0.

(11)

Hawking最初由于黑洞不能辐射能量，也不能具有熵，而反对Bekenstein的观点.然而由于对熵增根深蒂固的信仰，Bekenstein的坚持说服了许多物理学家[37-38].笔者认为科学失去了一次发展机遇.

目前黑洞的熵定义为：

(12)

它正比于黑洞视界的表面面积，其必然随着黑洞质量的增加而增加.

一个典型例子是黑洞蒸发的情况.量子效应导致黑洞蒸发，则黑洞的面积和相应的熵应该减少.更一般，Hawking结合广义相对论、黑洞热力学和量子力学得到著名的黑洞蒸发理论[39]和黑洞的熵增是相反的，因为相反的黑洞集聚物质和黑洞蒸发不可能都熵增.

此外，黑洞理论中具有许多神奇的结论，例如，Hawking定义黑洞温度为：

(13)

这个公式表明黑洞质量越大，温度越低；同时最小黑洞的温度约为10-7K.因此银河系中心的巨大黑洞的温度应该是非常非常低的.但我们认为在黑洞的收缩过程中巨大的势能将变为动能，应该具有较高的温度.物理学家已经讨论原始小黑洞，它们随收缩而更热，最后蒸发.

而且一般黑洞不能是一个孤立系统，它是一个开放系统，永远试图吸入更多物体.由此黑洞的热力学第二定律应该是不同的.一般说，这是一个只进不出的单向开放系统.它的质量只增不减，类似半开放的膜，相应于时间箭头和半群.但Hawking黑洞蒸发理论[39]中质量将减少.这一黑洞将是有进有出的双向开放系统.如此黑洞热力学应该是耗散结构理论，其熵是方程(14)，并且可能熵减.此外，笔者还讨论了天文学中各种可能的熵减，例如在天体演化中[40].

我们讨论了一般的非线性天文学和黑洞的非线性理论[41].笔者认为黑洞不可能收缩到奇点，因为当它收缩到10-15cm时，弱相互作用将出现，它将衰变，并且出现斥力.这可能相应于Hawking的黑洞蒸发理论[39].当半径连续缩小达到一个极限时，也许会经过弱相互作用而产生爆炸，例如作为gamma-射线爆(GRB)等.反之，如果这些不出现，可能理论将有重大变化，例如Pauli不相容(PEP)可能破缺等.这将反映出量子力学(弱相互作用)和广义相对论(黑洞)之间的巨大差别.

总之，目前的某些关于黑洞熵的讨论完全是基于对熵增的信仰.但黑洞的得到是一个简单化和有序化的过程，其最后只有三个参数(总质量M，总电荷Q和总角动量J).这意味着，当黑洞形成时，被压扁物质的所有别的性质都会丧失，许多可能性被简并，这样，熵和无序性将降低.这是最大的内部相互作用，可以形成一个中心，而且和熵增的气体扩散相反.这与我们提出的熵减观点是一致的[41-47].最后，对相反的黑洞和白洞，一个熵增，则另一个必然熵减.

5　任何系统演化的普适的熵变化公式

统计力学作为热力学的基础具有一个基本原理：统计独立性[42].笔者提出当孤立系统中存在各种内部相互作用时，统计独立性不再成立，相应的熵没有可加性，由此存在孤立系统中熵减的可能性[43，44]，其包括物理[30，45，46]、化学[47]、生物[48]、天文[40]和社会科学[49]等各方面，并且定量计算了某些例子[46].可喜的是笔者的这一观点现在已经开始得到国际上的某些学者的认同[50-52].

我们提出任何孤立系统中熵变化的普适公式是[44]：

dS=dSa+dSi，

(14)

其中孤立系统内部熵的可加部分是恒为正的dSa；而dSi是相互作用部分，可正可负.方程(14)类似于耗散结构理论中的公式：

dS=dSi+dSe.

(15)

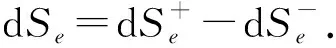
(16)

当

(17)

熵增dS>0，系统趋向无序.当

(18)

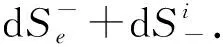
虽然对整个系统总熵是恒正的，并且在一个较长的时间系统可能也是熵增.但只要任何系统中存在不同的熵态，在从高熵态到低熵态的转化过程就应该出现熵减(图1中从A到B)[46]，例如从混沌到有序[53，54]，从战争到和平等等.如果这个系统可以作为孤立系统，则热力学第二定律将修改和发展.总之，从地球、生物到人类社会的各种演化不能永远都是无序过程.对吸引过程、内能及其转化、系统熵、非线性相互作用等，一个孤立系统可以形成具有较低熵的自组织结构[43-49]，例如自组装系统.

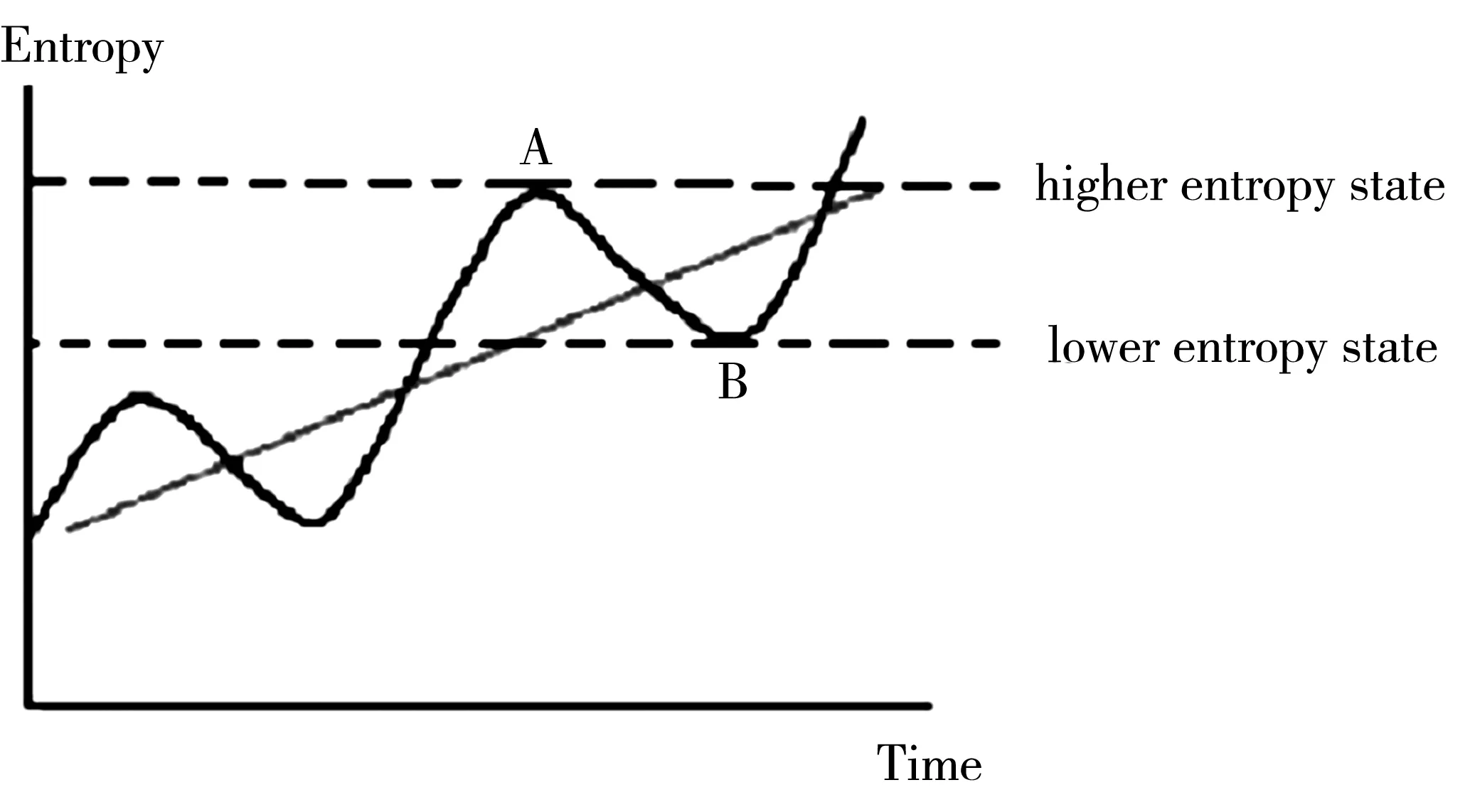
图1　具有较高熵和较低熵的态之间的转化过程Fig.1　Transformation processes between states with higher entropy and lower entropy.

广义相对论指出物质的质量和运动决定时空，反之时空又决定运动，其基本公式就是(1).这作为因果性的一个普适的物理表述，对现代社会科学是一个伟大的贡献，对此我们提出推广的社会广义相对论[55，56].每个人都具有命和运两方面，命是先天的时空和你的质量，运是你的活动和努力.“时势造英雄，英雄造时势”，二者互补，决定每个人的人生轨迹，同时形成波澜壮阔的大千世界.