辛普森悖论的范例

Bokai WANG, Pan WU, Brian KWAN, Xin M. TU, Changyong FENG,4,*

1.背景

考虑以下情况。假设来自DYC学区的两所学校，Alpha和Beta，的四年级学生参加了国家标准数学考试。 我们想比较这两所学校的平均分数。 假设我们已知Beta学校中男性和女性的平均分数分别高于Alpha学校男性和女性的平均分数。 那么这两所学校的整体平均分数如何？Beta学校的平均分数是否高于Alpha学校？ 答案似乎是肯定和直观的。更具体地说，假设每所学校的男女学生的平均分数如表1所示。

很明显，Beta学校的男女学生的平均分数都较高。但简单的计算表明，这两所学校的总体平均分数分别为83.2和81.8。Alpha学校的平均成绩更高！

表1. 两所学校的男女学生平均分数

假设Beta学校的学生接受了更先进的教学指导，改进了传统教学方法（Alpha学校采用传统教学方法）。直观地说，Beta学校中的学生会得到更好的平均分数。为什么这个例子如此违反直觉？ 这里有什么不对吗？平均分数是衡量学校学生表现的合理指标吗？ 事实上，当我们谈论两所学校时，大多数时候我们都假设这两所学校的男生比例大致相同。 很容易证明，如果上述两所学校男生的比例完全相同，并且Beta学校中男女学生的平均分数均高于Alpha学校中的男女学生平均分数，则Beta学校的总体平均分数更高。 我们的例子意味着性别比例的差异可能会扭转我们想研究的关系。

上述情况就是著名的辛普森悖论的例子[1]。不严格地说，辛普森悖论表明，条件关系（以每个学校的性别为例）并不意味着边际关系，反之亦然。尽管统计学界知道基于相同数据的条件和边际解释之间的“不一致性”，例如见Yule[2]，但辛普森悖论的影响远远超出了统计界。事实上，辛普森悖论在自然科学[3]、社会科学[4]，甚至哲学[5]等许多领域都非常普遍。我们甚至可以说它是观察性研究数据的固有属性[6]。

在本文中，我们讨论连续数据、分类数据和时间-事件数据中辛普森悖论的一些例子。 在第二部分中，我们使用条件期望给出辛普森悖论的一般统计解释。在接下来的两节中，我们通过例子展示辛普森悖论如何在分类数据和时间-事件数据中出现。第5节为结论部分。

2. 辛普森悖论和条件期望

我们知道，如果

a/b = c/d

那么

a/b = (a+c)/(b+d) = c/d,

(假设 b+d 0)，分数不等式是否具有类似的的性质？具体来说，假设sij，nij（i =1,2，j = 1,2）为正数，且

s1j/ n1j＜ s2j/ n2j, j = 1,2.

是否存在

(s11+s12) / (n11+n12) ＜ (s21+s22) / (n21+n22)?

辛普森[1]表示不一定。例如，

3/4 ＜ 7/9 和 2/3 ＜ 15/22

然而，

(3+2)/(4+3) = 5/7 ＞ 22/31 = (7+15)/(9+22)

这意味着汇总的数据显示出相反的关系。这是“辛普森悖论”的原始形式。 在本节中，我们构建了一个概率模型来研究为什么会出现这种逆转。

设 Y 是＜ 的 随 机 变 量。 假 设 X1和 X2是Xi∈{1,2,...,ki}的两个随机变量，其中ki( 2)，i = 1,2是正整数。 那么，对于任何m∈{1,...,k1}，

让我们将方程（1）与我们在第1节中的平均得分的例子联系起来。让X1= 1或2分别表示学校Alpha和Beta，X2= 1或2分别表示性别的男生和女生的。令Y表示

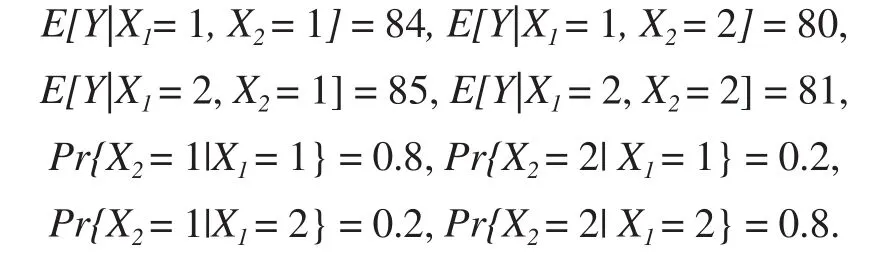
很明显

等式（2）表明，学校Beta中的男女学生的分数都更高。当我们计算每所学校的平均分数时，我们需要考虑性别因素。在（1）中我们可以看到，学校的平均分数是男性和女性得分的加权平均数，即

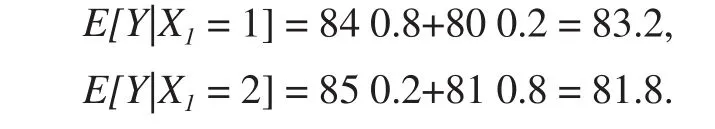
使用等式 (1)，我们发现

仔细研究数据表明，性别分布在扭转（2）至（3）中的不等现象方面起着重要作用。 很显然，如果（2）中的不等式成立，并且两所学校的男生比例相同，Beta学校的平均分数将高于Alpha学校的平均分数。

在这个例子中，性别在因果推断文献中被称为混杂因素[7]。 虽然新的教学方法提高了男生和女生的分数，但两所学校性别分布的不平衡可能会混淆新教学方法的效果。这在基于观察性研究的因果推断文献中被广泛研究，尤其是在流行病学中[6]。

上面的例子显示了辛普森悖论在连续性结果中是如何发生的。在以下两节中，我们将说明在分类数据和时间-事件数据中如何发生这种现象。

3.分类数据分析中的辛普森悖论

假设某种疾病的特征是可能不那么严重或更严重。患者可以选择去两家医院中的任何一家进行治疗：更好或普通的医院。治疗的结局是二分类的：成功或失败。考虑下面的例子。

我们可以看到，对于病情较轻的患者，较好的医院的治疗成功率远高于普通医院。病情更严重的患者结果类似。

我们从表2中再构建三个表。表3是治疗和结局的交叉分类。 两类医院的总体成功率分别为50/100和68/100。 这似乎表明，普通医院的成功率高于更好的医院。 这不是我们所期望的。

表2. 在不同严重程度的疾病中治疗结果的成功率

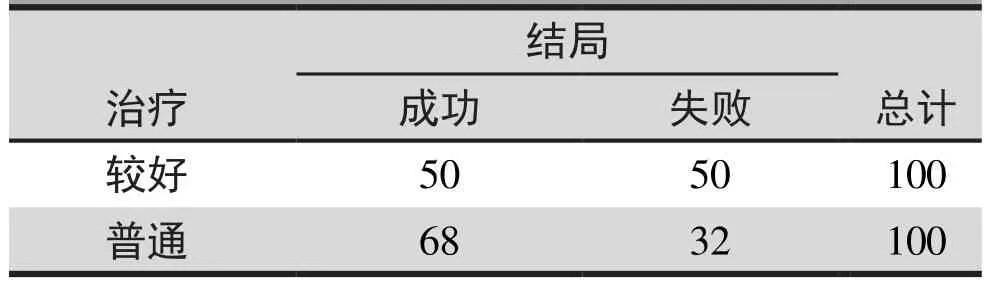
表3. 治疗和结局的交叉分类总结

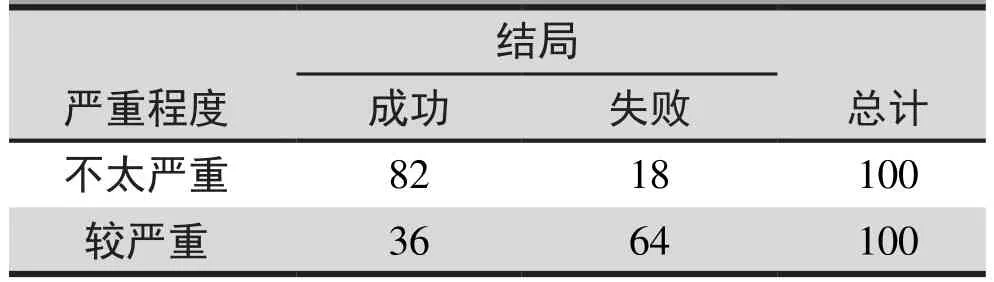
表4. 严重程度和结局的交叉分类总结

表4是严重程度和结局的交叉分类。 不太严重和较严重的患者的治疗成功率分别为82/100和36/100。这是合理的。

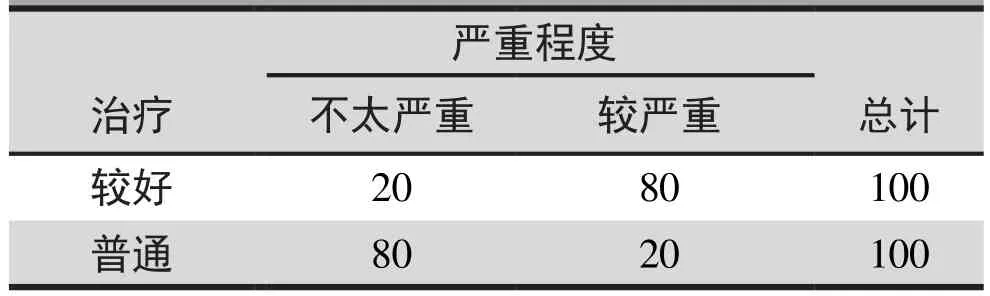
表5. 治疗和严重程度的交叉分类总结

表5是治疗和严重程度的交叉分类。 我们可以看到，较好治疗组中较严重患者的比例远高于普通治疗组。

令O表示结局，可能值为s（“成功”）或f（“失败”），T 表示治疗，可能值为b（“更好”）或n（“普通”），S表示严重程度，可能值为l（“不太严重”）或m（“更严重”）。那么

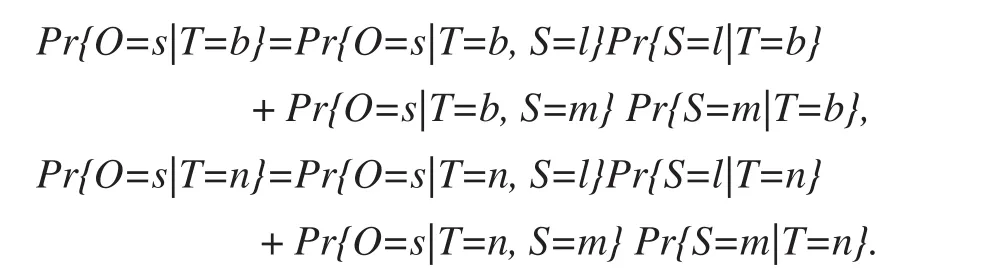
尽 管 表 2 明 显 显 示 Pr{O=s|T=b, S=l} ＞Pr{O=s|T=n, S=l} 且 Pr{O=s|T=b, S=m} ＞ Pr{O=s|T=n,S=m}，表 3 则显示 Pr{O=s|T=b} ＜ Pr{O=s|T=n}。从表4 和表5 我们知道，更严重的患者的治疗成功率远低于不太严重的患者，更好的治疗机构中更严重患者的比例比正常医院高得多。这种不平衡逆转了治疗效果的方向。

4.时间-事件数据分析中的辛普森悖论

辛普森悖论也可能发生在时间-事件数据中[8]。假设我们有两个治疗组（用X1表示：治疗(1)/对照(2)）。我们考虑两个年龄组X2= 1（或0），分别表示年龄 65（＞65）年。考虑治疗和年龄分类，假设患者的生存时间T的风险函数为

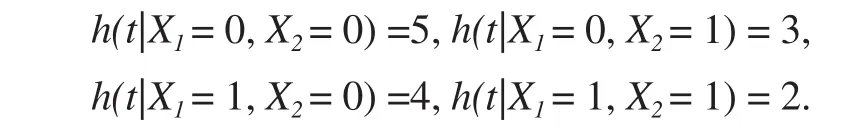
此外，我们假设治疗组的年龄分布是

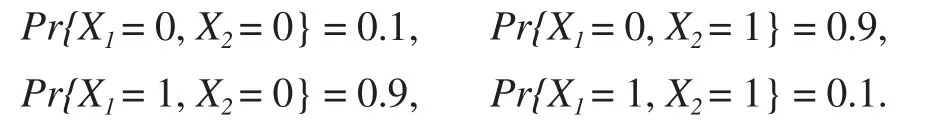
很明显，在每个年龄组中，治疗组的风险函数总是低于对照组的风险函数。 图1显示了每个年龄组中两个治疗组的风险函数。很明显，治疗组的效果优于对照组。

两个组别的边际风险函数分别是

h(t|X1= 0) = (0.5e-5t+2.7e-3t)/(0.1e-5t+0.9e-3t),

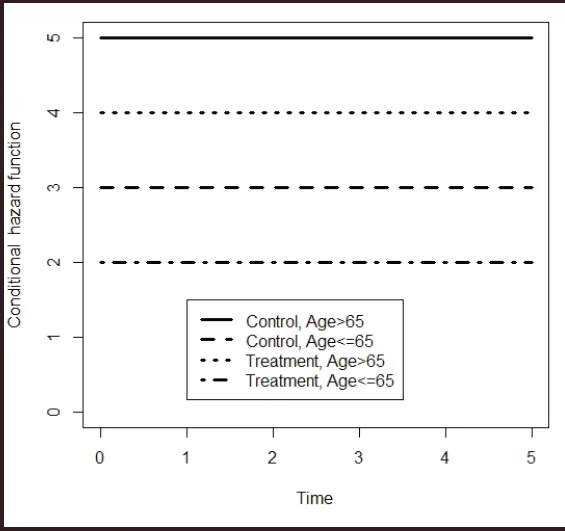
图1. 不同年龄组的风险函数

图2. 两组别的边际风险函数

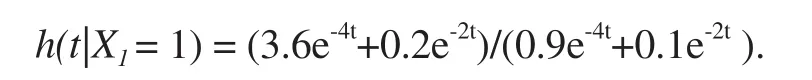
图2显示了整合年龄后两个组别的边际风险函数。在图1中，每个年龄组别内治疗组与对照组的风险比是恒定的。然而，边际风险比不再是一个常数。这可能会导致一些混杂，特别是如果某个时间点后的随访时间删失的情况。 在那种情况下，治疗组的估计风险函数可能远高于对照组，尽管这可能不是我们所预期的。

5.结论

由于混杂的影响，辛普森悖论在观察性研究中非常普遍。 在本文中，我们用一些例子来说明这种现象如何在连续性结果、分类结果和生存分析结果中出现。如果混杂效应没有得到适当解决，统计分析得出的结论可能是完全错误的。辛普森悖论的研究（或更一般地说，混杂因素的影响）形成了因果推论理论的标准，这尤其与大数据的错误相关。因为大多数据本质上是观察性的，如果没有解决混杂因素的话，混杂因素会掩盖我们感兴趣的关系。

资金来源

本研究没有获得任何外部资助。

利益冲突

作者报告没有与本文相关的利益冲突。

作者贡献

Bokai Wang, Changyong Feng, 和 Xin M. Tu: 理论推导；

Pan Wu 和 Brian Kwan: 撰写文章。

1. Simpson EH. The Interpretation of Interaction in Contingency Tables. J R Stat Soc Series B. 1951; 13: 238-241

2. Yule GU. Notes on the Theory of Association of Attributes in Statistics. Biometrika. 1903; 2 (2): 121-134. doi: https://doi.org/10.1093/biomet/2.2.121

3. Heydtmann M. The nature of truth: Simpson’s Paradox and the limits of statistical data.QJM.2002; 95(4): 247-249. doi:https://doi.org/10.1093/qjmed/95.4.247

4. Lerman K. Computational social scientist beware: Simpson’s paradox in behavioral data. J Comput Soc Sc. 2018; 1: 49-58.doi: https://doi.org/10.1007/s42001-017-0007-4

5. Malinas G, Bigelow J. Simpson’s Paradox. Edward N. Zalta(ed.) The Stanford Encyclopedia of Philosophy (Fall 2016 Edition). Available from: https://plato.stanford.edu/archives/fall2016/entries/paradox-simpson

6. Rosenbaum P R. Observational Studies (2nd ed.). New York:Springer; 2002

7. Pearl J. Causality (2nded.). Cambridge University Press;2009

8. Cox DR. Regression Models and Life-Tables. J R Stat Soc Series B Stat Methodol. 1972; 34(2): 187-220