双离合自动变速器系统建模与代码自动生成的研究
陈 亮 郝洪涛 倪凡凡 严 冬宁夏大学 机械工程学院 宁夏银川 750021
0 引言
随着车辆操纵自动化的快速发展,汽车自动变速器正呈现出蓬勃发展的趋势。双离合自动变速器作为一种新型的自动变速器,既保持了传统变速器结构简单、传动效率高等优点,又能够实现在无动力中断的情况下转换传动比,缩短换挡时间,有效的提高了换挡品质,从而改善了车辆行驶的舒适性,具有广阔的发展前景[1~2]。
1 DCT结构及其工作原理
选择性输出双离合自动变速器采用双中间轴式机构,如图1所示,其传动装置由两根带有同步器装置的输入轴(C1和C2轴)、两根平行布置的中间轴(m1和m2轴)、布置在输出轴上的两个平行布置的离合器、多个同步器装置、多个换挡拨叉、一个倒挡轴以及一个差速器组成。两根输入轴分别为一根空心轴和一根实心轴,空心轴空套在实心轴上,一端分别与离合器C1和C2相连接,使用选择性输出的方式将变速器奇、偶数挡输出齿轮分别布置在两根中间轴上,其中奇数挡位与离合器C1相连,偶数挡位与离合器C2相连,通过双离合器的交替接合以及切换不同的同步器状态来实现无动力间断换挡,经由不同输出轴实现扭矩变换和输出。
车辆在空挡时,所有同步器处在中位,两个离合器的从动部分和主动部分均是分离的。当车辆起步时,以1挡升2挡为例,这时1挡同步器和1挡齿轮啮合,1挡传递的扭矩大于车辆的行驶阻力,车辆开始起步。当车速继续增加,到达了升挡点时,2挡同步器和2挡齿轮啮合,同时变速箱控制单元(Transmission Control Unit,简称:TCU)控制离合器C2的油压P2开始增大,使得离合器C2开始慢慢接合,同时离合器C1的油压P1开始减小,离合器C1逐渐分离,当离合器C2完全接合、离合器C1完全分离时,整个换挡过程结束,保证了换挡过程中发动机的转矩被连续传递到车轮,其余升、降挡换挡过程与此类似[3]。此外,DCT在正常运行过程中,总有两个挡位几乎是同时挂入的,其中一个为工作挡位,另一个为预挂挡位。变速箱控制单元根据车辆的运行状态确定预挂挡位,即判断下一预挂挡位为当前挡位的高一挡位还是低一挡位。

图1 DCT结构简图
2 汽车动力学建模
双离合自动变速器系统研究的第一步是根据具体的被控对象建立控制算法模型。本文的控制系统需要首先建立车辆动力学模型。本文采用前向建模的方法对整车动力系统进行建模,具体的控制框图详见图2,所建立模型包括:发动机模型、自动变速器模型、换挡控制模型及车辆动力学模型等。

图2 DCT系统控制原理图
2.1 发动机模型
发动机模型的建立是研究车辆传动系统的基础,作为整车传动系统的动力源,发动机不断地向其他组件输出转矩,因此建立恰当的发动机模型对汽车系统的研究有着重要意义。本文选择以节气门开度和发动机转速两参数值作为该系统模型的输入值,以转矩和角速度作为输出值。选择在有载动态工况下,发动机动态输出扭矩与稳态输出扭矩的关系可以近似的表示为:
(1)
(2)
式中:n为发动机转速;ωe为发动机角速度;γ为扭矩下降系数(取0.07~0.09);Te为发动机稳态输出扭矩;Ted为发动机动态输出扭矩。
根据上式(1)和(2),在Matlab/Simulink软件模块下建立发动机有载动态仿真模型,如图3所示:

图3 发动机模型
从图中可以看出,此仿真模型以发动机的二维特性表为核心,并将实验所得的相关数据存储到特性表中,通过输入相应的节气门开度和发动机转速值,利用图表插值的方法得到发动机输出转矩值。另外,发动机输出转速值也是通过反馈信号的形式作为发动机特性表的输入信号。
2.2 双离合变速器模型
双离合变速器换挡过程的核心问题就是两个离合器工作状态的相互交替,该过程的动态仿真涉及到离合器动态转矩传递特性和离合器工作状态的切换两个关键问题。然而,汽车的行驶工况相对复杂,换挡过程中影响因素较多且行驶环境很难预测,为了研究方便,对涉及的双离合变速器这一复杂连续的多质量、多自由度系统作如下简化:1)假设传动系统是由无惯性的弹性环节和无弹性的惯性环节构成;2)忽略由同步器移动和离合器接合分离引起的轴的横向移动;3)不考虑齿轮啮合弹性、轴承与轴承座的弹性、系统的阻尼和间隙,简化后双离合变速器可视为一个离散系统。
其中,双离合变速器传递转矩的大小取决于离合器压力、离合器结构尺寸和摩擦特性;在车辆换挡过程中,一般把DCT换挡过程按两个离合器的工作状态分为5个阶段[4]:低挡传动阶段-低挡转矩阶段-惯性阶段-高挡转矩阶段-高挡传动阶段;其对应的动力学模型可分别描述为:
(1)低挡传动阶段:离合器C1完全接合,离合器C2无油压。
(3)
(2)低挡转矩阶段:C1完全接合,C2处于滑摩状态;
(4)
(3)惯性阶段:C1处于滑摩状态,C2处于滑摩状态;
(5)
(4)高挡转矩阶段:C1处于滑摩状态,C2完全接合状态;
(6)
(5)高挡传动阶段:C1无油压,C2完全接合状态
(7)
其中,离合器从动盘转速与变速器输出转速之的关系为:
(8)
符号函数为:
(9)
转速差:Δω=ωe-ωc
(10)
上式中:Tc3为发动机输出动态转矩;Ie为发动机转动惯量;Tc1、Tc2分别为离合器C1和C2输出转矩;Ic1、Ic2分别为离合器C1和C2从动盘惯量;ωc1、ωc2分别为离合器C1和C2从动盘转速;ic1g、ic2g分别为奇、偶数轴对应挡位传动比;i0为主减传动比;Tout为变速器输出扭矩;ud为离合器动摩擦系数;A为离合器活塞作用面积;P1、P2分别为离合器C1和C2的油压;Z为离合器摩擦面数;r11、r12、r21、r22分别为离合器C1和C2摩擦片的内外径;ωo为变速器输出转速;sign为符号函数;Δω为离合器主从盘转速差。根据上述五个阶段所列数学表达式和给定的双离合变速器各挡位的传动比,如表1所示,经整理得出的双离合变速器系统模型如下图4所示。

表1 变速器各挡传动比的参数表

图4 变速器系统仿真模型
2.3 换挡控制逻辑模型
Matlab/Simulink模块中有很多图形化的参数用于表示逻辑控制和逻辑关系,那么就需要一种软件作为工具来对这种关系进行识别;其中的Stateflow就能很好的解决这个问题,它既能识别图形化的逻辑控制关系,又能和Simulink仿真实现完全兼容。本文在Simulink仿真软件的基础上,采用Stateflow来简洁的描述换挡模型的逻辑控制和逻辑关系。
换挡逻辑控制模块用于控制车辆在何时进行换挡。它提前存储了车辆的换挡规律,以当前车速、升/降挡点的车速为输入信号,并不停的与车辆当前的状态进行比较,当车辆的状态符合它既有的换挡规律中达到的换挡条件时,车辆的换挡规律模型就被激活,车辆根据换挡规律进行换挡;同时,根据当前的挡位状态和车速,预测出下一挡位状态,以确保换挡的准确性。本文中换挡逻辑模块采用Stateflow[5]建立了图5为换挡规律存储模块和换挡逻辑控制模块的Simulink模型,图6为换挡逻辑控制的Stateflow图,并设置了换挡的逻辑判断原理,能够让各相邻挡位互相转换,图7为简单的换挡控制流程图,用来说明车辆的具体换挡控制过程,以当前挡位n挡为例进行自动换挡策略流程分析,当前汽车正在以n挡行驶,当驾驶员意图发生变化导致车速和节气门开度发生变化时,如驾驶员踩油门加速,则当前条件满足n挡预挂n+1挡时,n+1挡同步器与n+1挡齿轮啮合,即预挂n +1挡,若驾驶员继续踩下加速油门踏板,则进行离合器的切换,完成n+1挡行驶,n挡降n-1挡的原理与之相同。

图5 换挡逻辑控制
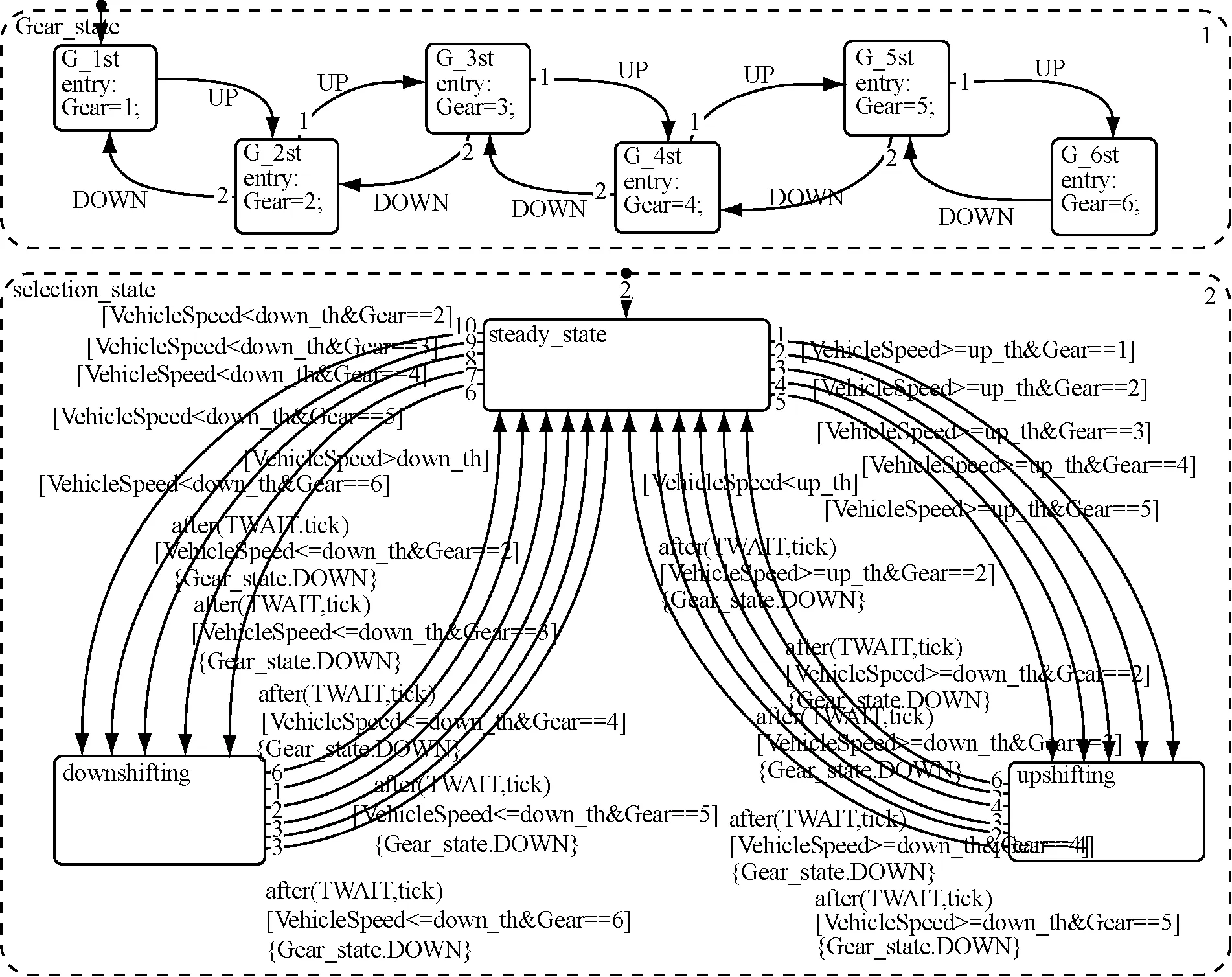
图6 换挡逻辑控制的Stateflow
2.4 整车动力学模型
本文从建模角度出发,考虑汽车整车主要动力学模型,对整车模型做了相应的简化:1)在无风状态下行驶,不考虑风速产生的行驶阻力;2)忽略汽车行驶过程中的任何方向的摆动;3)选择汽车行驶路面为平整路面,不考虑坡度的影响。
汽车行驶时需要克服的阻力主要有以下几部分:
Ft=∑F=F+FW+Fi+Fj
(11)
2.4.1 滚动阻力
车辆在行驶时,轮胎与路面的接触会产生切向、法向的相互作用力和相应轮胎与路面的变形;其中法向作用力主要是重力的作用,而切向作用力会阻碍车轮向前运动形成一种阻力。由于具有相互作用力,轮胎和路面都会发生变形,但一般情况下,轮胎和路面相比,路面的变形可以忽略不计,主要是轮胎的变形,变形时轮胎内部也会有相互摩擦,会消耗部分功[6],这种由于轮胎的摩擦迟滞损失就相当于阻力偶,于是就产生了滚动阻力:
Ff=mgf·cosα
(12)

2.4.2 空气阻力
车辆在行驶的过程中,由于空气的压力作用会产生一个阻碍车辆前进的力,所以称之为空气阻力。它主要来自于空气作用在汽车外表面上的压力的法向分力和摩擦阻力,应为:
(13)
2.4.3 坡度阻力
汽车在上下时,汽车重力沿着坡道会产生一个分力,这个力就称为汽车的坡道阻力,应为:
Fi=mgsinα
(14)
2.4.4 加速阻力
汽车加速行驶过程中会产生惯性力,行驶过程中需要克服自身加速惯性力,即产生了加速阻力。应为:
(15)
综上分析可得转矩与各参数之间的关系可以表示为:
(16)
又变速器输入与输出扭矩的对应关系为:
Tout=igi0Ted
(17)
因此,联立(16)和(17)式可得汽车动力学表达式为:
(18)
上述式中:m为整车质量;f为滚动阻力系数;α为路面坡度(取α=0);CD为空气阻力系数;A为迎风面积;ρ为空气密度;v为汽车行驶的速度;δ为汽车旋转质量换算系数(取δ=1.3);ηT为传动系统的机械效率;ig为变速器某一挡位传动比;i0为主减传动比;r为汽车车轮半径。
根据上述所得的汽车动力学方程表达式,利用Simulink模块建立汽车运动学模型如图8所示:
2.5 系统仿真模型
如图9所示,将以上建立的各个模型按照逻辑关系进行整理,并且对比较复杂的模型进行封装后,建立起包含该双离合器自动变速器的整车动力传动系统仿真模型,并命名为“Newmodel.mdl”。
3 自动生成代码
3.1 RTW自动程序创建过程简介
实时工作空间(Real-Time Workshop,简称:RTW)的实现机制是一个复杂的过程,它不仅提供了一个实时的开发环境,还提供目标语言编译器(Target Language Compiler,简称:TLC)来扩充自己的功能,通过使用TLC,可以修改和优化RTW生成的C程序。RTW自动程序创建过程能在不同主机环境下生成实时应用程序,创建过程使用高级语言编译器中的联编实时程序来控制所生成的源代码的编译和链接[7~8]。同时它还使用一个高级的M文件命令控制程序的创建过程,默认命令是make_rtw。如图10所示,代码创建过程大致包括[9]:

图8 汽车动力学模型

图9 整车系统模型

图10 RTW代码自动创建过程
(1)分析Simulink模型并对模型的描述文件进行编译;本阶段,RTW先通过读取模型文件(model.mdl)并对其进行编译,形成模型的中间描述文件(model.rtw)。
(2)由目标语言编译器TLC从模型中生成代码;本阶段,目标语言编译器将中间描述文件转换为目标指定代码。
(3)程序联编文件(makefile)的生成;本阶段主要是生成自定义联编文件,即model.mk文件,目的在于指导联编程序如何对从模型中生成的源代码或主程序,或如何对用户提供的模块进行编译。
(4)在自定义程序创建文件的控制下,由联编实用程序生成可执行程序。本阶段中,用户可以选择定制目标系统类型来生成源代码,然后使用特定的开发环境对代码进行交叉编译并完成将其下载到目标硬件中。
3.2 生成实时代码
仿真及代码自动生成过程包括确定仿真输入输出信号、设置仿真参数,最后进行动态仿真和目标代码转换。本文以整车动力传动系统模型“Newmodel.mdl”为例,将该模型通过RTW自动生成C代码。
3.2.1 参数设置
在将仿真模型利用RTW生成C代码时之前,首先进行相应的设置;包括对仿真的时间范围进行设定,仿真时间包括起始和停止时间、仿真步长和选择合适的仿真解法。具体的设置过程如下:打开如图11所示参数对话框,在Solve界面设置仿真时间为10s,设置Solve option区域中的Type为Fixed-step,设置Solve为ode8(Dormand-Prince)求解器,设置Fixed Step Size为0.01,其它参数均选择默认值。

图11 Solve界面中的参数设置
选择了仿真步长和合适的仿真解法后,还应选择目标代码类型,在图12所示的对话框中,单击System target file栏对应的Browse按钮,出现如图3所示的对话框,则可以从中选择所期望转换后生成的目标代码类型,这里选择Visual C/C++Solution file for simulink code,并选中tout和yout前的复选框。

图12 实时工具目标选择对话框
3.2.2 生成C代码
打开名为“Newmodel.mdl”模型的系统参数对话框,启动如图13所示的界面,选择System target file为grt_tlc,并选中Create code generation report和Open report automatically复选框,指定模板文件,其余类似的设置这里不再赘述;设置好编译环境后,单击Ctrl+B或Build按钮,即可生成C代码。其中的Ctrl+B或Build命令用于调用目标文件grt_tlc,使用指定的模板文件来生成联编文件(makeflie),然后RTW会利用这个联编文件来建立程序,最后真正地实现由模型转换成可执行代码如图14所示;同样地,RTW在代码生成和程序创建过程中产生的主要文件有:Newmodel.c:模型单机源代码;Newmodel.h:含有状态变量和参数的包含头文件;Newmodel_date.c:是对模型中所用到的参数进行赋值的C代码;Newmodel.mk:是创建可执行程序的连编文件;Newmodel.exe:是生成的实时可执行代码;Newmodel.mat:是用于保存系统状态、输出和时间等数据的文件;在这些文件中,每个文件都执行了一定的功能。

图13 RTW界面中的参数设置

图14 从模型到自动生成的C代码
4 仿真结果分析
4.1 系统模型仿真
汽车系统Simulink仿真模型建立完毕后,在此基础上进行了DCT整车系统离线仿真,本文选取发动机的油门开度参数值为0.5,运行“Newmodel.mdl”模型,分别得到了发动机转速、汽车车速、当前挡位的实验结果,如图15所示,其仿真结果与理论分析基本一致。



图15 Simulink模型的仿真结果
通过对整车动力系统模型的离线仿真,还证明了所建模型能正确反映当挡位发生变化时对应的转矩和速度等参数的变化,能够实现挡位预测和自动换挡等功能。
4.2 代码验证
完成由模型到C代码的自动转换后,选择以发动机油门开度参数0.5为输入信号,发动机转速、挡位和车速为输出信号,运行在由Simulink的RTW生成的Newmodel.mk文件,并采用相应程序来读取Newmodel.mat文件,确保Newmodel.mat文件中包含数据变量被保存Matlab工作空间中,最后根据所设置的变量输入程序指令得到了如图16所示的结果;


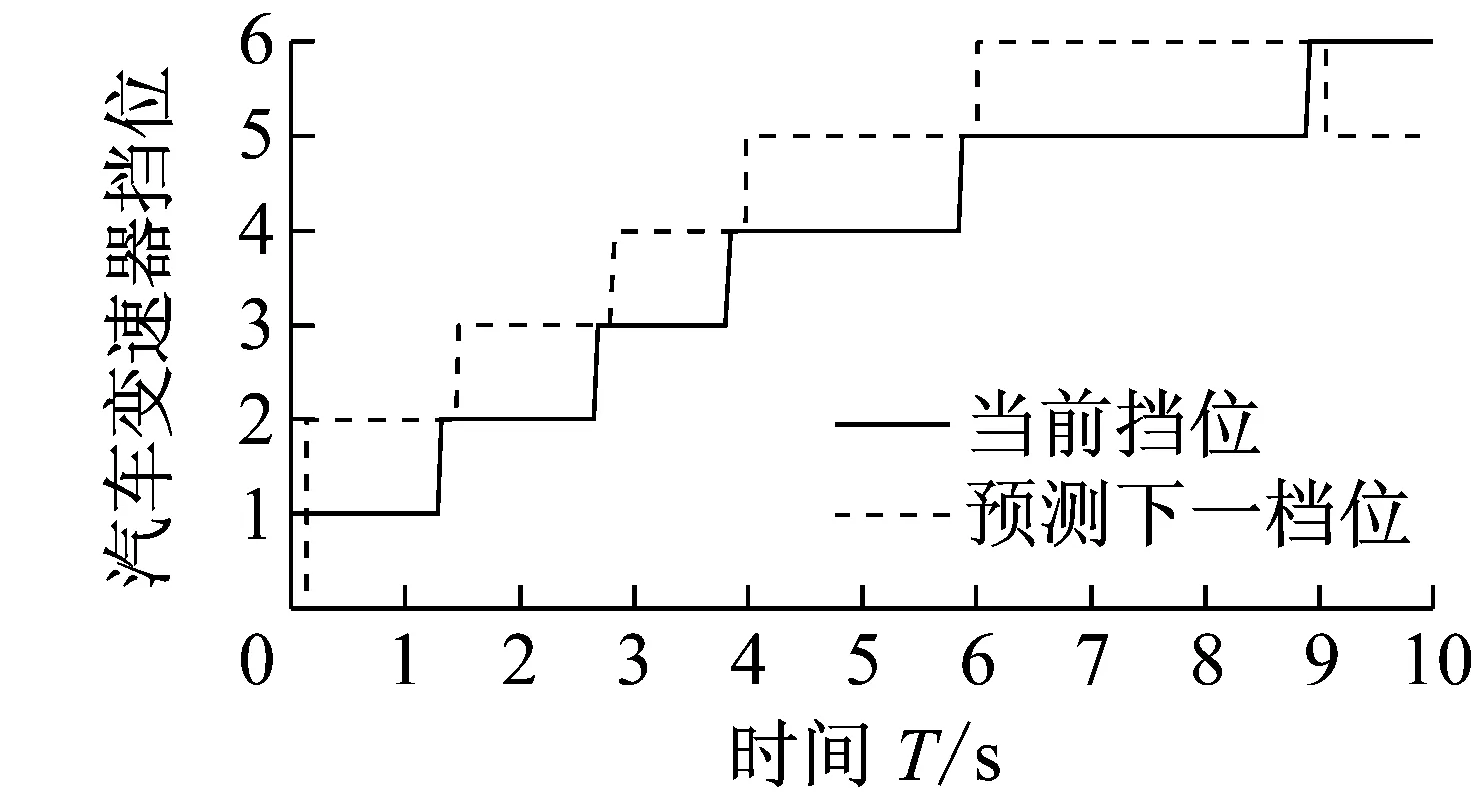

图16 可执行C代码的仿真结果
4.3 结果对比
完成从模型到代码的自动转换后,将生成的可执行C代码与Simulink模型进行性能比较,选择以发动机转速和汽车车速信号为例,将代码的计算结果与模型的计算结果进行比较,如图17所示,由输出结果可知,Simulink模型结果与实时程序代码计算结果完全一致。


图17 仿真结果对比
为了进一步验证二者结果是否一致,允许在Matlab命令窗口中输入以下代码:
输入: >> max(abs(ESpeed - rt_Espeed));
max(abs(Vspeed - rt_Vspeed));
输出误差值:ans= 1.0e-12 *
0 0.2274
ans= 1.0e-14 *
0 0.1776
从以上结果可以看出;这两种方法所得的计算结果误差很小,数量级基本在13~15左右,误差分析结果如图18所示,横坐标表示采样矩阵为一维矩阵,纵坐标表示两种结果的误差值,由上述方法可进一步证明模型仿真结果和C代码仿真结果是完全一致的。

图18 误差分析

图19 ControlDesk快速原型仿真结果
为了更进一步检验仿真结果的一致性,这里选择以dSPACE实时系统为平台,处理器板硬件为DS1202,编译器为DSP C Compile,dSPACE车用硬件为MicroLabBox,系统目标文件选择rti1202.tlc,其他的设置步骤同上,利用RTW及dSPACE提供的RTI进行模型的编译,从而实现由模型到C代码再到可执行代码的转变。将C代码进而生成硬件可识别的可执行代码,过程中产生多个文件,其中的“Model. sdf”为最终编译结果文件,也是需要下载到硬件中的文件,利用ControlDesk软件建立快速原型测试界面,并下载已经生成的可执行代码到dSPACE硬件,用于快速原型仿真试验和验证,仿真结果如图19所示,经分析,模型仿真结果和可执
行代码仿真结果完全一致。
最后,经由以上三种方法的仿真分析与比较,证明了汽车动力传动系统模型建立的合理性和RTW生成代码的正确性。并且由模型转换成C代码的过程中没有进行代码的编辑,从而减轻了用户编写代码的工作量。
5 结束语
本文依据发动机、双离合变速器及整车各部件之间的结构原理和数学关系,以Matlab/Simulink软件为仿真平台,建立了整车传动系统动力学模型,在此基础上又进行模型实时仿真分析,研究其控制策略,并通过对此系统的仿真结果分析,证明了该模型能够比较准确地模拟换挡过程中的动态特性,仿真结果验证了所建立数学模型的合理性和可行性;同时也提高了DCT动力系统设计的效率。此外,利用Matlab所提供的RTW、dSPACE提供的RTI和目标语言编译器等工具实现了Simulink模型到目标代码的直接转换,并进行代码仿真结果的验证和快速控制原型试验验证。最后将三者的仿真结果作了比较,结果表明该方法是正确可行的。这样不仅缩短了开发周期,降低了编程的强度和难度,而且也为后续的DCT换的规律与控制策略的研究提供了方法和理论基础,对整个DCT项目的进行起到十分重要的作用。
[1] 张金乐,马彪,张英锋,等. 双离合器自动变速器换挡特性与控制仿真[J]. 农业机械学报,2010,41(5):6-11.
[2] 朱耀文,王其东,孙保群,等. 选择性输出的双离合器自动变速器建模及仿真分析[J]. 合肥工业大学学报:自然科学版,2012,35(2):157-160.
[3] 刘振军,胡建军,李光辉,等. 模糊神经网络的自动变速汽车换挡规律分析[J]. 重庆大学学报,2009,32(8):897-903.
[4] 金伦,程秀生,孙俐,等. 双离合器自动变速器仿真研究[J]. 汽车技术,2005(8):4-7.
[5] 曹亦俊,赵跃民,温雪峰,等. 废弃电子设备的资源化研究发展现状[J]. 环境污染与防治,2003,25(5):289-292.
[6] 孙永丽. 基于DSP的轮胎压力监测系统研究与开发[D]. 山东理工大学,2009.
[7] 周俊杰. Matlab/Simulink实例详解[M]. 中国水利水电出版社,2014.
[8] 黄永安,马路,刘慧敏,等. Matlab7.0/Simulink 6.0建模仿真开发与高级工程应用[M]. 清华大学出版社,2005.
[9] 李强,王民钢,杨尧,等.快速原型中Simulink模型的代码自动生成[J]. 电子测量技术,2009,32(2):28-31.

