推力轴承瓦面造型对承载性能影响的分析与验证
刘 渊 俞翔栋 李建军 李岳峰 顾智超(中船重工第七一一所 动力装置事业部, 上海 201108)
0 引言
推力轴承是船舶动力系统中的关键设备,主要功能是将船舶推进器产生的推力或拉力传递给船体,以使船舶前进或后退。随着船舶向着大型化发展,要求推力轴承能够承受更大的载荷,致使推力轴承具有更大的结构尺寸。同时,船舶对于功能的需求日益提高,需要搭载的设备也越来越多,设备空间紧张。尤其是近年来随着船舶行业的迅速发展,使得推力轴承结构尺寸的增大与设备空间紧张的矛盾日趋突出[1],急需提出合理有效的解决方法,在有限的结构空间内提高推力轴承的承载能力。
提高推力轴承的承载能力需要对轴承进行改进[2-5]。一方面是探寻新材料,通过改变推力瓦的材料以承受更大的轴承比压,改善润滑性能。另一方面是对轴承的结构进行改进,主要包括宏观结构和微观结构的改进。宏观结构的改进主要是指推力瓦支承形式的改变,例如将固定瓦改为可倾瓦,将刚性支承改为弹性支承、非接触式支承等,达到提高轴承承载能力的效果。微观结构的改进主要体现在推力瓦表面织构和瓦面造型的设计。
长期以来,国内外的学者们在推力轴承瓦面造型研究方面做了一定的工作。陈志澜[6]运用瓦面二次曲面数学模型和三维热弹流润滑性能分析软件,分析了斜面、圆柱面、马鞍面等多种型面对润滑性能的影响,认为沿周向凸起及沿径向下凹的瓦面造型有利于形成收敛油楔。高磊等[7]提出了一种新型的柱面弧形油楔推力滑动轴承,确定了参数的最佳取值范围。Sharma等[8]对抛物线型、摆线型等四种固定瓦进行了实验研究,结果表明摆线型轮廓的承载力得到了显著的提高。M.Fillon等[9]建立了初始型面为锥形推力轴承的TEHD模型,研究表明初始型面对油膜厚度、温升具有较大影响,对于功耗的影响不大。Sharma等[10]还建立了不同油膜温度分布模型进行分析,研究表明勒记德多项式所得的数值解更符合实际工况。
本文针对斜面瓦、斜面平台瓦、阶梯瓦、二次抛物线型瓦(微凹)、二次抛物线型瓦(微凸)、摆线型面瓦等六种瓦面造型开展研究,建立了不同瓦面造型的数学模型,基于数值计算软件MATLAB计算并分析了瓦面造型对推力轴承承载性能的影响。定量描述了结构参数对承载性能的影响,并获得了结构参数的最优值。建立了以推力瓦温度作为评价指标的试验方法,并开展对比试验验证。这为推力轴承瓦面造型的优化设计提供了依据,对于大功率推力轴承的结构优化具有一定的借鉴作用。
1 数学模型
假设油膜流动为层流,油膜在推力瓦瓦面无滑移,油膜压力在油膜厚度方向上不变,不计入表面粗糙度的影响,同时将问题视为无限宽滑块问题,不考虑端泄,则Reynolds方程简化为一维常微分方程,此时雷诺方程可简化如下:
(1)
无量纲雷诺方程为:
(2)
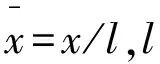
将无量纲雷诺方程差分后化为代数方程得:
(3)
采用有限差分法(中心差分)得:
边界条件:
由式(3)可知,当膜厚方程已知时,根据雷诺方程可以求得压力的通解,再代入边界条件即可得到压力分布情况。运用一定的数值算法可进一步求得油膜的承载力、最大油膜压力等特性参数。
油膜承载力:
(4)
其中,N为节点数。
最大油膜压力:
Pmax=max(P)
(5)
2 瓦面造型对承载性能的影响
2.1 瓦面造型建模
求解压力分布情况,首先需要建立各造型瓦面的膜厚数学方程。本文分别建立了斜面瓦、斜面平台瓦、阶梯瓦、二次抛物线型瓦(微凹)、二次抛物线型瓦(微凸)、摆线型面瓦的数学模型,具体方程如下:
斜面瓦膜厚数学方程:
(6)
斜面平台瓦膜厚数学方程:
(7)
阶梯瓦膜厚数学方程:
(8)
二次抛物线型瓦(微凹)膜厚数学方程:
(9)
二次抛物线型瓦(微凸)膜厚数学方程:
(10)
摆线型面瓦膜厚数学方程:
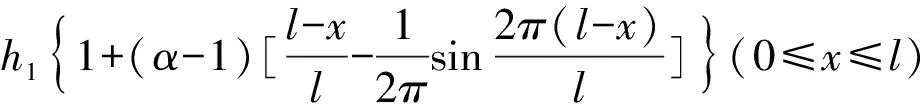
(11)
其中,h1为最小油膜厚度;h2为最大油膜厚度;l为推力瓦中径的周向长度;l1为造型分界位置;α为轴承间隙比,即α=h2/h1。
六种瓦面造型的几何模型如图1所示。
2.2 承载性能计算
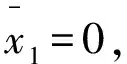
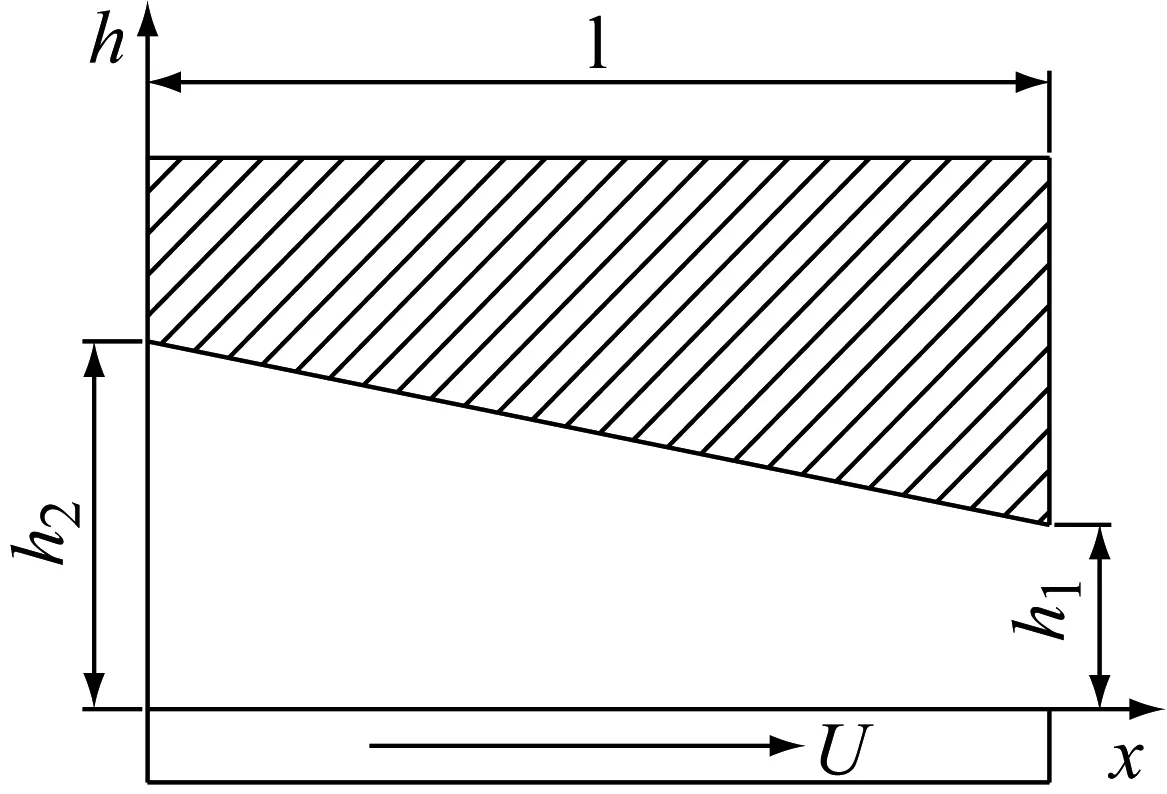
a)斜面瓦
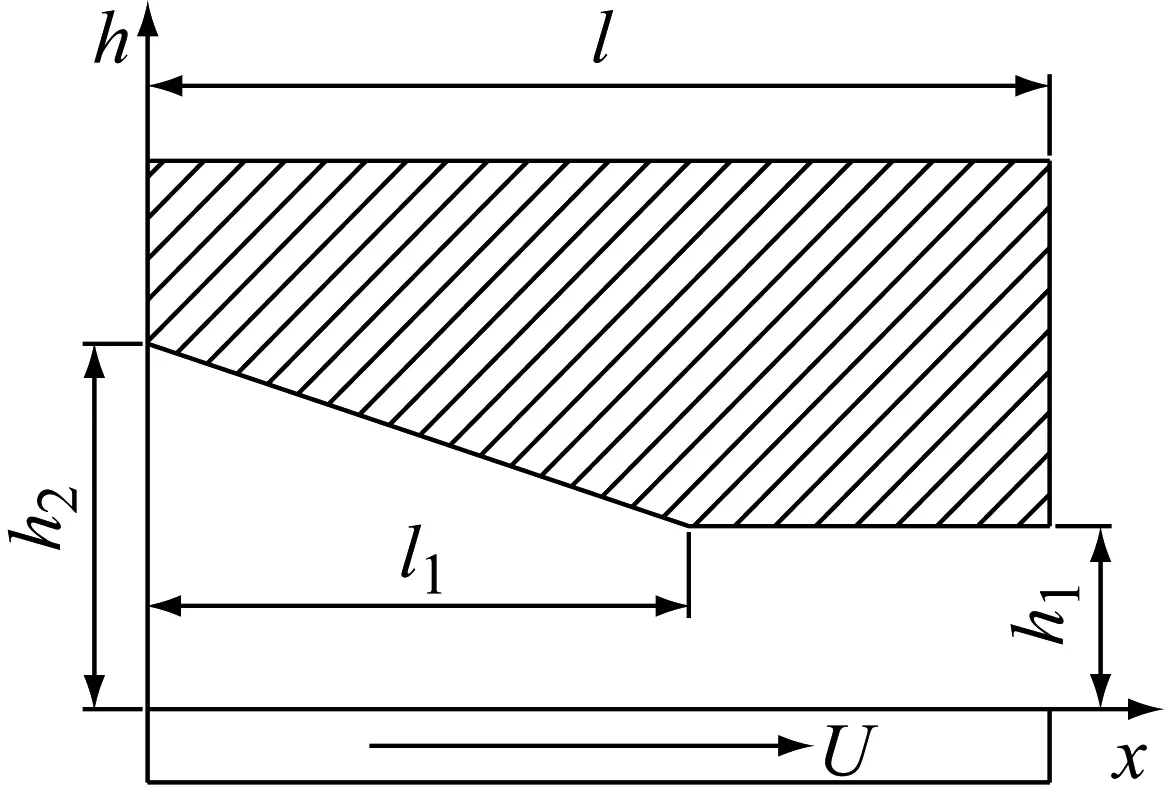
b)斜面平台瓦
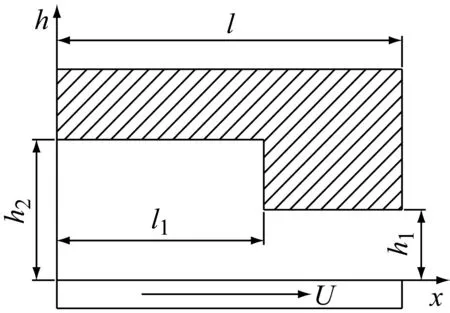
c)阶梯瓦
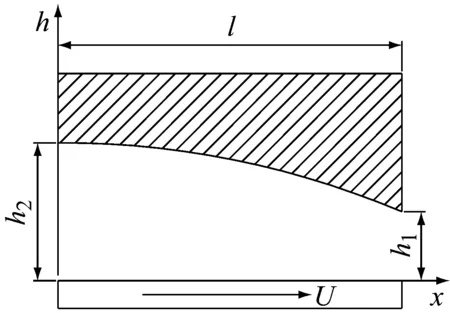
d)二次抛物线型瓦(微凹)
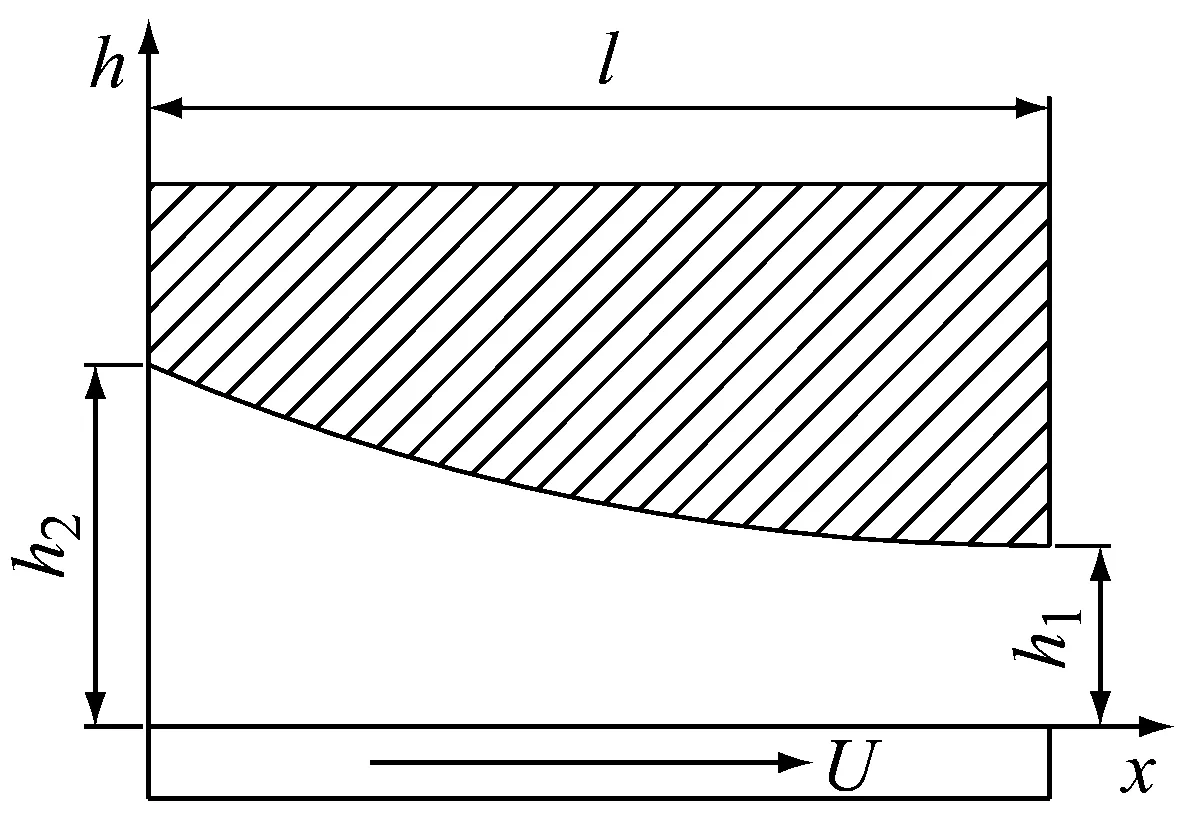
e)二次抛物线型瓦(微凸)
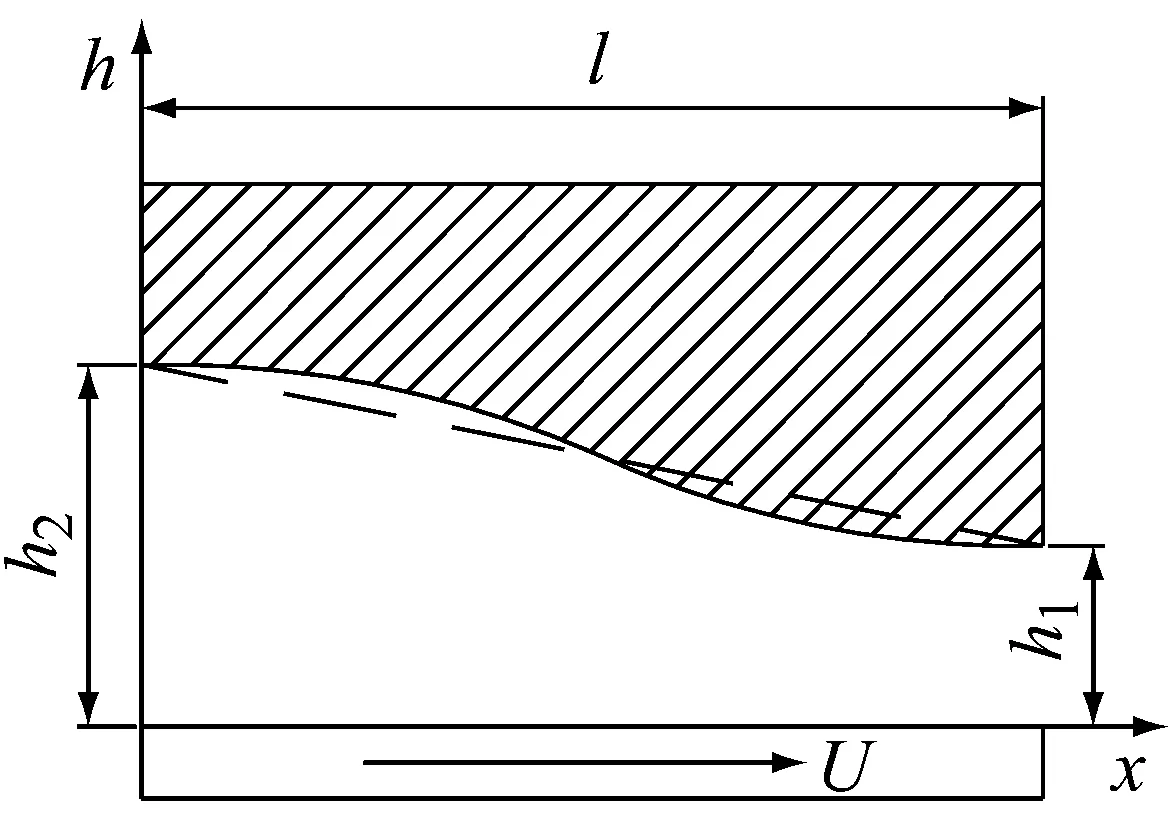
f)摆线型面瓦
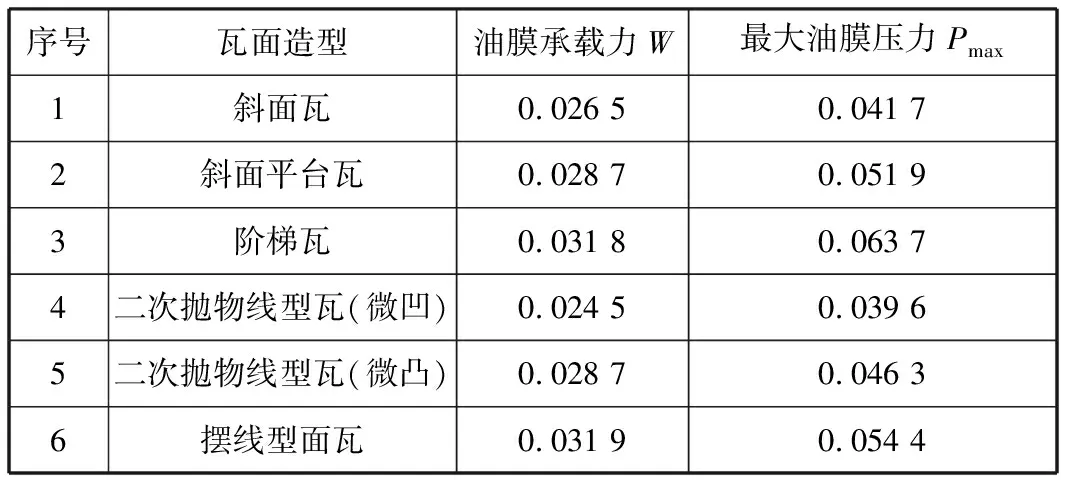
表1 不同瓦面造型承载性能的比较
由表1可以看出,斜面平台瓦、阶梯瓦、二次抛物线型瓦(微凸)、摆线型瓦的油膜承载力较大,均优于斜面瓦,其中摆线型瓦的油膜承载力最大,达到了0.031 9,与斜面瓦相比提高了20.4%。其次,阶梯瓦的油膜承载力与摆线型瓦相近,达到了0.031 8。比较各瓦面造型产生的最大油膜压力,阶梯瓦产生的最大油膜压力最大,达到了0.063 7,与斜面瓦相比增大了52.8%,摆线型面瓦次之,也达到了0.054 4,相比斜面瓦增大了30.5%。
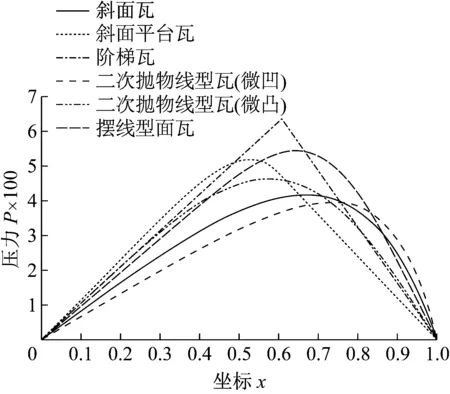
图2 无量纲油膜压力分布情况Fig.2 The distribution of dimensionless oil film pressure
由图2可知,阶梯瓦的油膜压力分布梯度较大,基本呈尖峰状分布,最大油膜压力出现在瓦面造型分界位置附近。摆线型面瓦等其余五种造型的油膜压力呈抛物线型分布,压力变化平缓,最大油膜压力出现在靠近油楔出口侧。
综上所述,摆线型面瓦能够提供更高的油膜承载力,产生较大的最大油膜压力,且压力变化平缓,呈抛物线型分布,具有良好的承载性能,是一种较优的瓦面造型。然而这是一种曲面造型,对于加工精度要求极高,需要达到与油膜厚度同等数量级的精度要求。由上述分析已知,斜面平台瓦和阶梯瓦的承载性能均优于斜面瓦,瓦面造型为多个平面构成,利于工业生产。由式(7)和式(8)可以看出,油膜厚度随结构参数取值的变化而变化,进而影响油膜压力的分布情况。
2.3 造型分界位置对承载性能的影响
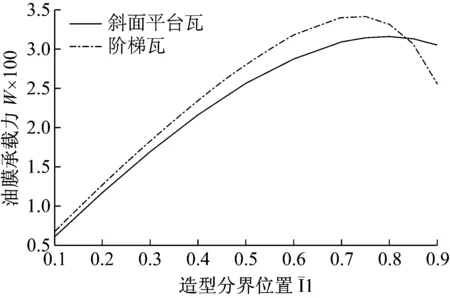
图3 油膜承载力与造型分界位置的关系Fig.3 The relationship between oil film load capacity and boundary point
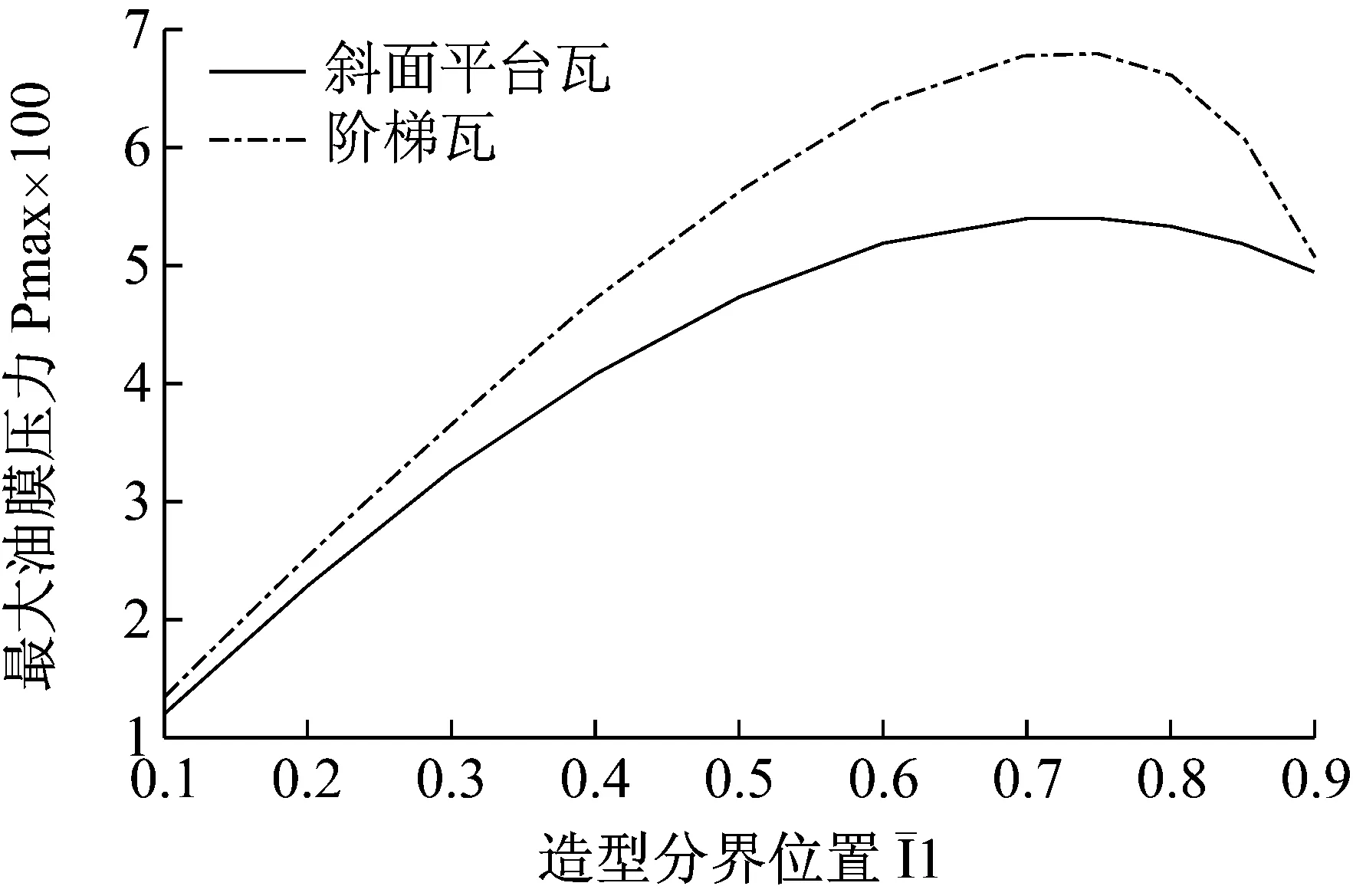
图4 最大油膜压力与造型分界位置的关系Fig.4 The relationship between maximum oil film pressure and boundary point
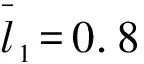
2.4 间隙比对承载性能的影响
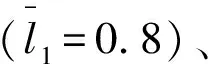
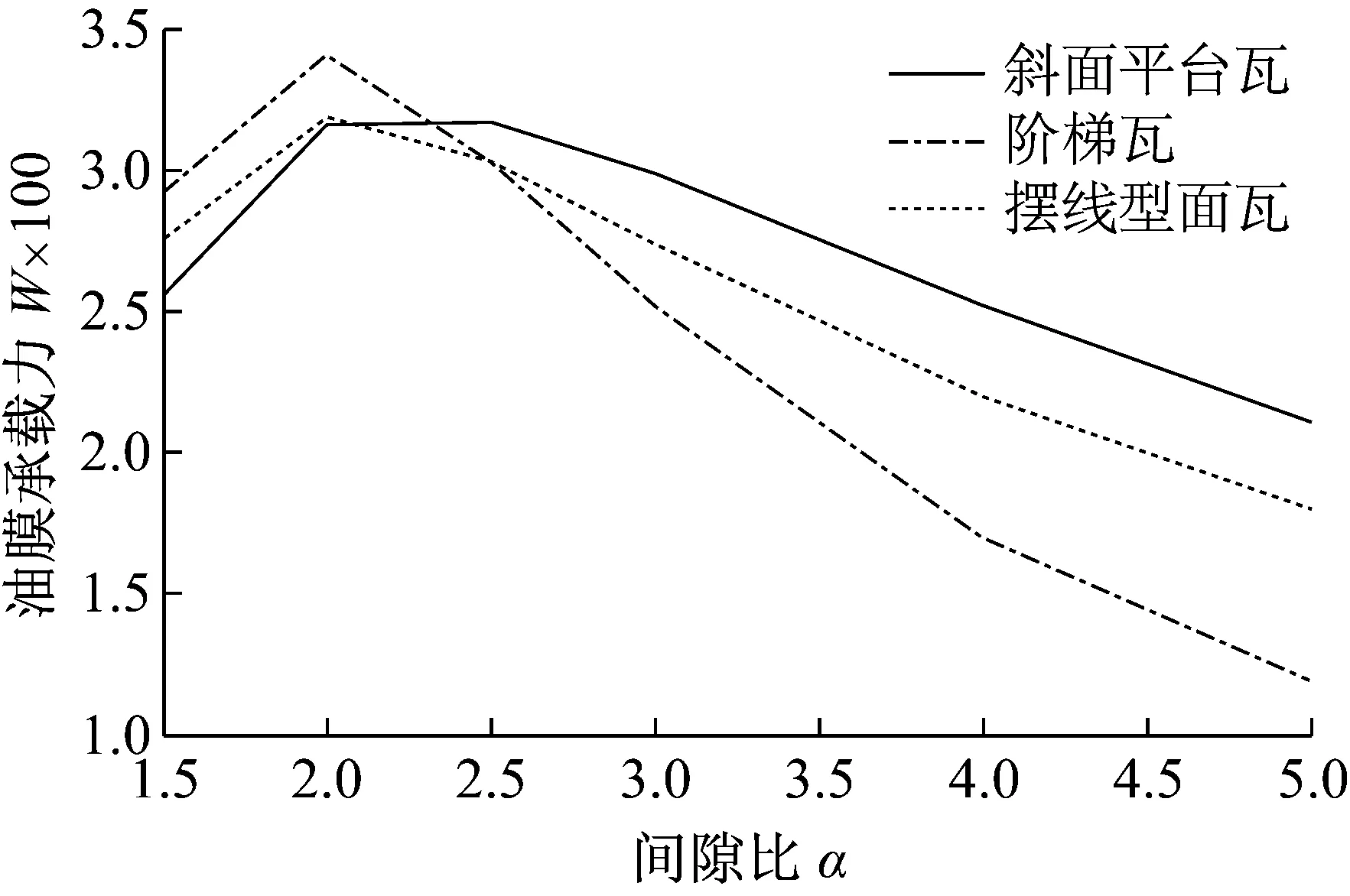
图5 油膜承载力与间隙比的关系Fig.5 The relationship between oil film load capacity and clearance ratio
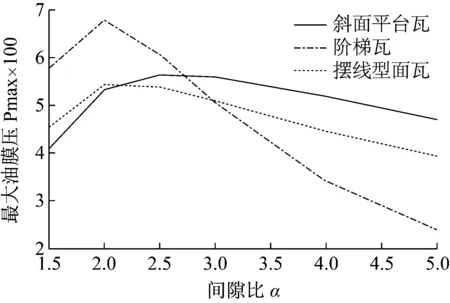
图6 最大油膜压力与间隙比的关系Fig.6 The relationship between maximum oil film pressure and clearance ratio
由上图可以看出,随着间隙比的增大,三者的油膜承载力和最大油膜压力均呈现先增大再减小的趋势,并且在间隙比为2附近达到最大。由此可见,针对该三种瓦面造型,间隙比设计在2附近时承载性能最优。
2.5 承载性能对比
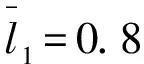
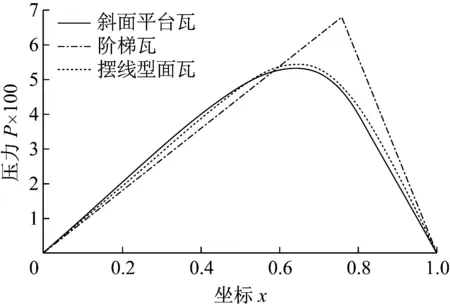
图7 无量纲油膜压力分布情况Fig.7 The distribution of dimensionless oil film pressure
由上图可见,当取最优结构参数时,斜面平台瓦和阶梯瓦的承载性能均有所提高。使得斜面平台瓦能够达到与摆线型面瓦相近的承载性能,油膜压力分布呈抛物线型状,压力变化平缓,最大油膜压力出现在造型分界位置靠油楔入口侧;阶梯瓦与摆线型面瓦相比,能产生更高的油膜承载力和更大的最大油膜压力,然而油膜压力分布呈尖峰状,压力分布梯度较大,最大压力出现在造型分界位置附近。
综上可知,取最优结构参数的斜面平台瓦具有较优的综合承载性能,并且利于工业生产。
3 试验验证
开展斜面平台瓦与斜面瓦的对比试验。以TL300Q型推力轴承作为试验样机搭建试验平台,试验台布置如图8和图9所示。保持润滑条件不变的前提下,分别安装取最优结构参数的斜面平台瓦和斜面瓦进行推力轴承运转试验,根据运行工况施加相应载荷,并采用PT100温度传感器和数据采集监控系统采集推力瓦的温度值,通过电控箱上的数显表读取数值。将测试结果分别填入试验表格,如表2和表3所示。
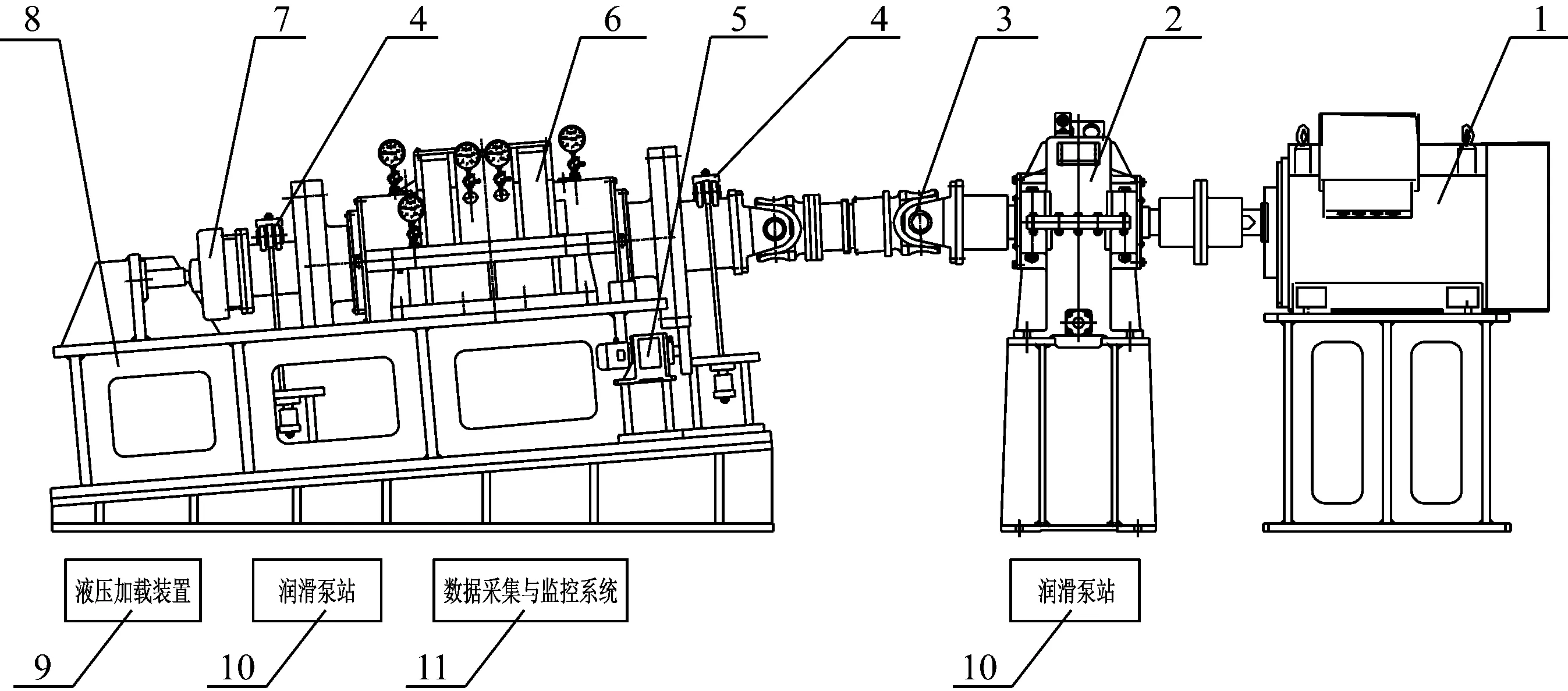
1. 驱动装置系统; 2. 齿轮箱; 3. 万向联轴器; 4. 径向加载装置; 5. 盘车装置; 6. 推力轴承样机; 7. 轴向加载装置; 8. 试验台架; 9. 液压加载装置; 10. 润滑泵站; 11. 数据采集监控系统

图9 试验台布置图Fig.9 Experiment arrangement
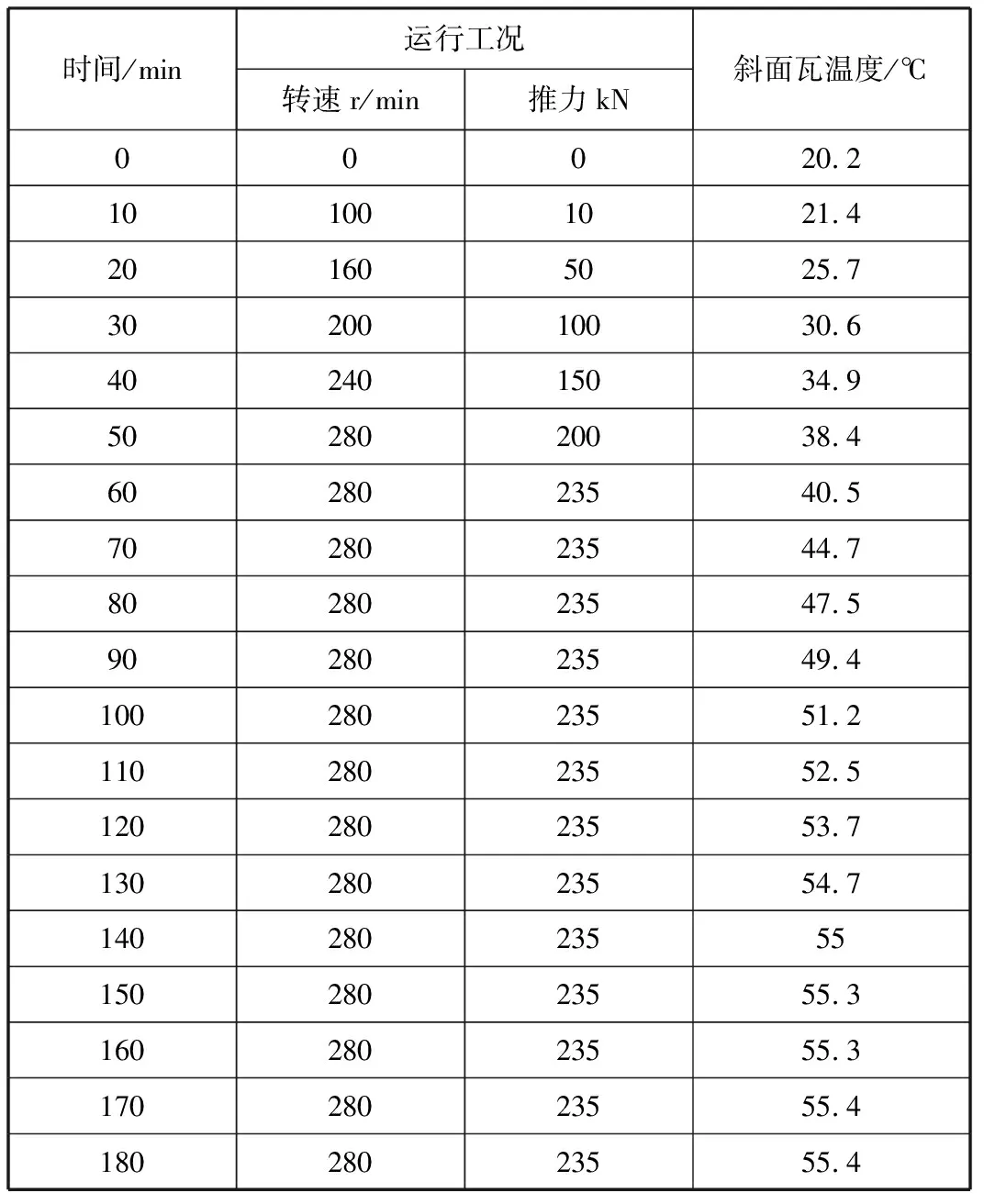
表2 斜面瓦推力轴承运转试验记录
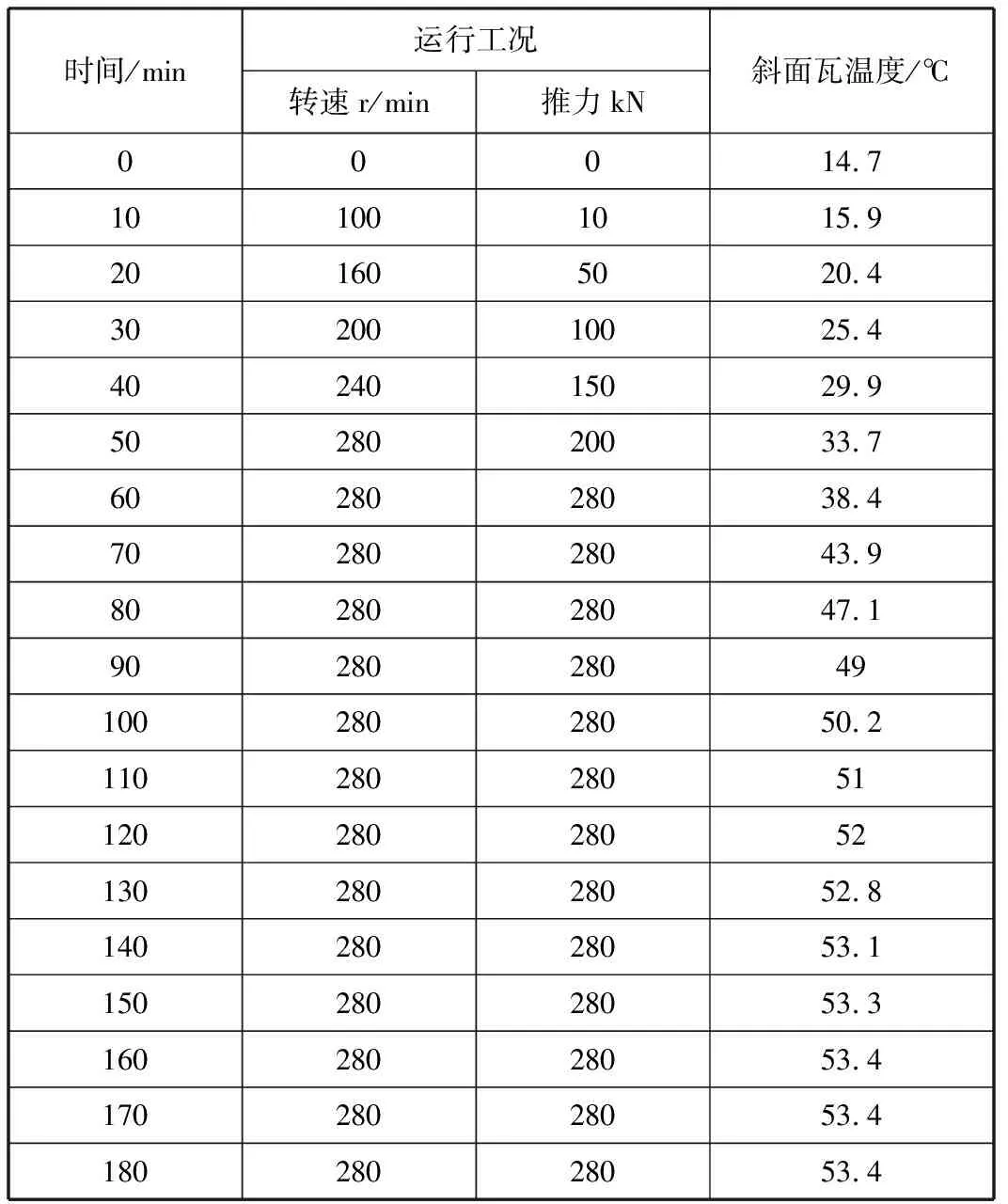
表3 斜面平台瓦推力轴承运转试验记录
建立两种瓦面造型的时间-推力瓦温度曲线,并绘制在同一图表中进行对比分析,如图10所示。由图可见,随着转速和推力的增加,推力瓦温度将产生明显的变化,最终当运行工况保持不变,推力瓦温度也将趋于平稳。转速保持一致,当斜面瓦、斜面平台瓦分别施加235 kN和280 kN时,瓦块温度分别稳定在55.4℃和53.4℃。由此可见,斜面平台瓦具有更优的承载性能,当载荷增加19.1%,斜面平台瓦的稳定温度仍不高于斜面瓦。

图10 推力轴承运转试验记录Fig.10 Running test record of the thrust bearing
4 结论
(1)本文基于数值计算软件MATLAB,建立了推力轴承瓦面造型承载性能的分析方法,分析对比了六种瓦面造型的承载性能。结果表明,瓦面造型对于推力轴承的承载性能具有影响。其中,摆线型面瓦的承载性能最优,然而加工难度较大;斜面平台瓦和阶梯瓦的承载性能也优于斜面瓦,并且利于工业生产。
(2)针对斜面平台瓦和阶梯瓦开展了详细分析,获得了结构参数的最优值。使得斜面平台瓦能达到与摆线型面瓦相近的承载性能,并且压力变化平缓;阶梯瓦能产生更高的油膜承载力和更大的最大油膜压力,然而压力分布梯度较大。
(3)开展了斜面平台瓦与斜面瓦的对比试验,建立了以推力瓦温度作为评价指标的试验方法,结果表明取最优结构参数的斜面平台瓦具有较优的综合承载性能。这为推力轴承瓦面造型的优化设计提供了依据,对于大功率推力轴承的结构优化具有一定的借鉴作用。
[1] 胡荣华. 船用滑动推力轴承结构设计研究[J]. 船舶工程,2007,29(5):60-64.
HU R H. Structural design research of the marine thrust bearing[J]. Ship Engineering,2007,29(5):60-64.
[2] 司占博,王松,郭杨阳. 水润滑推力轴承推力瓦应力场分析[J]. 润滑与密封,2012,37(6):57-59.
WANG Z B, WANG S, GUO Y Y. .Analysis on Thrust Watts Stress Field of Water Lubrication Thrust Bearing[J]. Lubrication Engineering,2012,37(6):57-59.
[3] 李忠,王风才,袁晓阳,等. 螺旋面扇形瓦推力轴承热动力润滑性能分析[J]. 机械科学与技术,1999,18(3):409-411.
LI Z, WANG F C, YUAN X Y, et al. Thermohydrodynamic Analysis of a Helicoid Sector-shaped Pad Thrust Bearing[J]. Mechanical Science and Technology,1999,18(3):409-411.
[4] 何春勇,刘正林,吴铸新. 潜水泵水润滑推力轴承润滑性能数值分析[J]. 润滑与密封,2010,35(8):59-62.
HE C Y, LIU Z L, WU Z X. Numerical Analysis of Lubricating Property of Submersible Pump Water-lubricated Thrust Bearing[J]. Lubrication Engineering,2010,35(8):59-62.
[5] 蒋秀龙. 可倾瓦推力滑动轴承弹流润滑研究[D]. 浙江::浙江大学,2011.
[6] 陈志澜. 巨型推力轴承的三维热弹流动力润滑性能研究[D]. 西安:西安交通大学,1998.
[7] 高磊,刘俊,安琦. 柱面弧形油楔推力滑动轴承数值分析[J]. 润滑与密封,2007,32(8):99-102.
GAO L, LIU J, AN Q. Numerical Study on the Thrust Bearing with Cylinder Arc Pad Face[J]. Lubrication Engineering,2007,32(8):99-102.
[8] Sharma R K,Pandey R K. Experimental studies of pressure distributions infinite slider bearing with single continuous surface profiles on the pads[J]. Tribology International,2009,42:1040-1045.
[9] Fillon M,Glavatskih S B. PTFE-faced centre pivot thrust pad bearigs:Factors affecting TEHD performance[J]. Tribology International,2008,41(12):1219-1225.
[10] Sharma R K,Pandey R K An investigation into the validity of the temperature profile approximations across the film thickness in THD analysis of infinitely wide slider bearing[J]. Tribology Online,2006,1(1):19-24.

