基于同步压缩小波法的行波故障测距应用研究

陈雅芳，蔡世翔（.广州中光电气科技有限公司，广东 广州 50660；.广东电网公司云浮供电局，广东 云浮 57300）

0 引 言

随着电力系统规模的逐渐加大，国民对用电可靠性和运行稳定性的要求越来越高。所以，要减少电力系统运行故障的发生，且需在电力系统发生故障后快速、准确地定位故障并排除故障。快速准确的故障测距定位是电力系统安全稳定运行的前提条件，可以有效提高线路巡线人员的工作效率，减小停电造成的各种经济损失，具有重大的社会经济效益[1]。行波测距不易受系统参数、线路负荷等外界条件干扰，定位速度迅速且测距精度较高，是近年来输电线路故障测距的发展方向与研究热点之一。

1 同步压缩小波变换原理

小波分析被认为是在傅里叶分析基础上的重大发展。它在时域和频域都有很好的局部化特性，因此在计算机视觉、数据压缩和信息编码解析等众多应用学科领域得到了广泛应用。本文利用信号在不同尺度上小波变换的Lipschitz指数、模极大值来表征信号的突变特点，即利用信号的奇异性对电力线路行波故障测距进行研究和应用。

同步压缩小波[2-3]支持信号重构，且时频分辨率比传统小波方法高，原理如下。

对于信号x(t)，它的傅里叶变换可表示为：

其中，ω代表角频率，其反变换为：

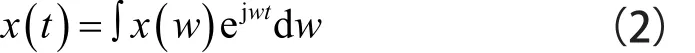
则信号x(t)可以表示为一组不同频率的谐波之和。这种现象可以表述为式（3），对信号s(t)有：

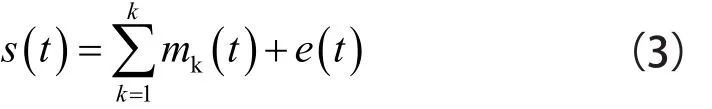
式中，mk(t)=Akcos(φ(t))表示第k个时变谐波成分，其中Ak(t)表示信号的瞬时振幅，φk(t)表示第k个谐波成分的瞬时相位；e(t)表示扰动或噪声。

由相位求导得到瞬时频率fk(t)：

将小波变换重新计算至频率域，得到：

式中，a为尺度因子，b为时间平移因子，ξ为角频率，ψ^( ξ) 为母小波的傅里叶变换。

将单一谐波信号s(t)=Acoswt进行小波变换，结果为：

若母小波的主频是w0，那么其小波系数谱理论上集中在尺度a=w0/w的位置，即母小波与子小波的频率之比。实际上，即使小波系数在尺度方向存在扩散现象，但由于其相位是保持不变的，所以针对小波系数WS(a,b)可以计算其瞬时频率：

其中，arg(·)为小波系数的相位。

同步压缩小波变换是通过计算瞬时频率，把小波系数从(b,a)投影到(b,ωs(a,b))。而对于离散情况，尺度坐标和频率坐标都是离散值(Δak=ak-ak-1，Δwl=wlwl-1)。因此，同步压缩小波变换的公式可以表示为[4]：

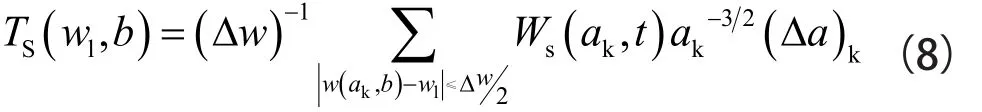
其中，ak为尺度坐标(k=1,2…)，wl为频率坐标（l=1,2…）。

由于同步压缩小波变换在频率方向将复小波系数进行了重新排列，因此该过程是可逆的。将其进行逆变换，结果为：

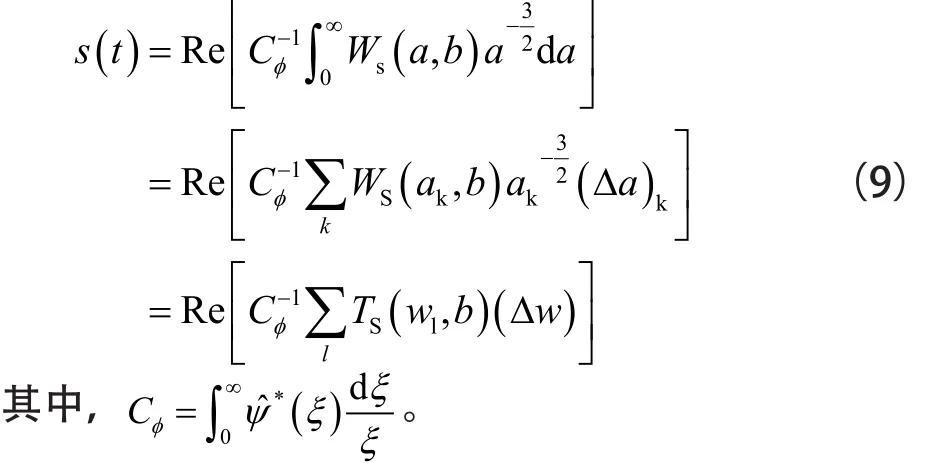
2 理论信号分析

首先对一组合成信号进行验证分析，以验证同步压缩小波变换的高分辨率特性。合成信号波形如图1所示，该信号是由一个频率为50 Hz、幅值为1的正弦波和一个频率为100 Hz、幅值为1的正弦波叠加而成。合成信号进行小波变换，结果如图2所示。对合成信号进行同步压缩小波变换，结果如图3所示。对比以上两种小波变换的结果可以看出，同步压缩小波变换具有更高的分辨率。

图1 合成信号波形

图2 合成信号小波变换结果

图3 合成信号SWT结果

综上分析，因为同步压缩小波变换在数学上是可逆的，所以通过对信号的反变换可完全恢复处理前的原始信号。对信号的同步压缩小波结果进行反变换，结果如图4所示。可以看出，重构信号与变换前的原始信号基本重合，重构误差很小[5]。

图4 SWT反变换结果与原始信号

3 仿真分析

3.1 不含噪情况

为了验证该方法对电力系统单相接地故障电压数据分析的效果，在仿真软件MATLAB上搭建了双端线路模型M-N进行双端行波测距。测距流程图如图5所示，M端电压线模分量如图6所示，M端α模分量SWT结果如图7所示，对得到的SWT变换做反变换的结果如图8所示。可见，结果基本与原始信号吻合，符合SWT的数学特性。

图5 SWT双端测距流程图

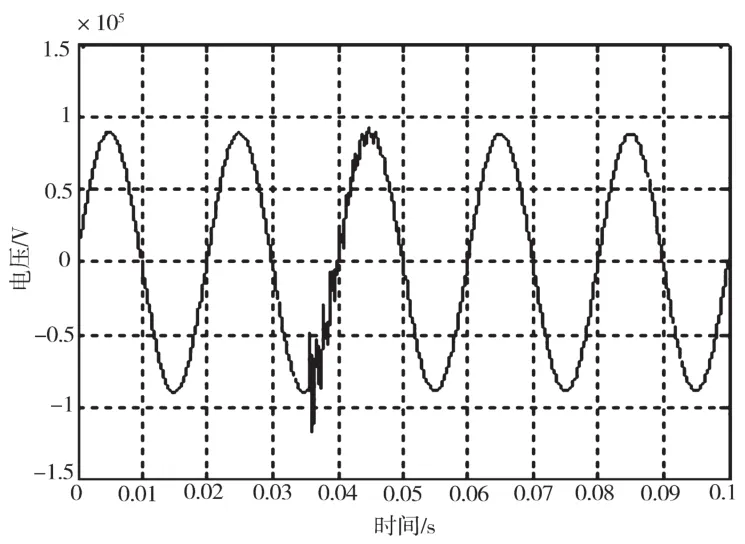
图6 M端α模分量

图7 M端α模分量SWT结果

图8 SWT反变换结果

得到四端的30 kHz故障行波分量波形，如图9所示。

图9 不同端30 kHz故障行波分量波形图

得到M、N、T1和T2四端的初始行波波头到达时 间 分 别 为 0.035 40 s、0.035 2 s、0.035 44 s和0.035 09 s。下面采用SWT的多端测距结果与小波变换（CWT）测距结果进行比较，结果如表1、表2所示。可见，SWT变换与CWT相比，测距精度与计算速度获得了大幅提高。

3.2 含噪声情况

在模型中附加40 dBW，对其线模分量进行SWT，结果如图10所示。

最终得到的测距结果为25.18 km，误差180 m，表示同步压缩小波法可以准确定位故障位置。

表1 采用SWT的多端网络故障测距仿真结果

表2 采用CWT的多端网络故障测距仿真结果

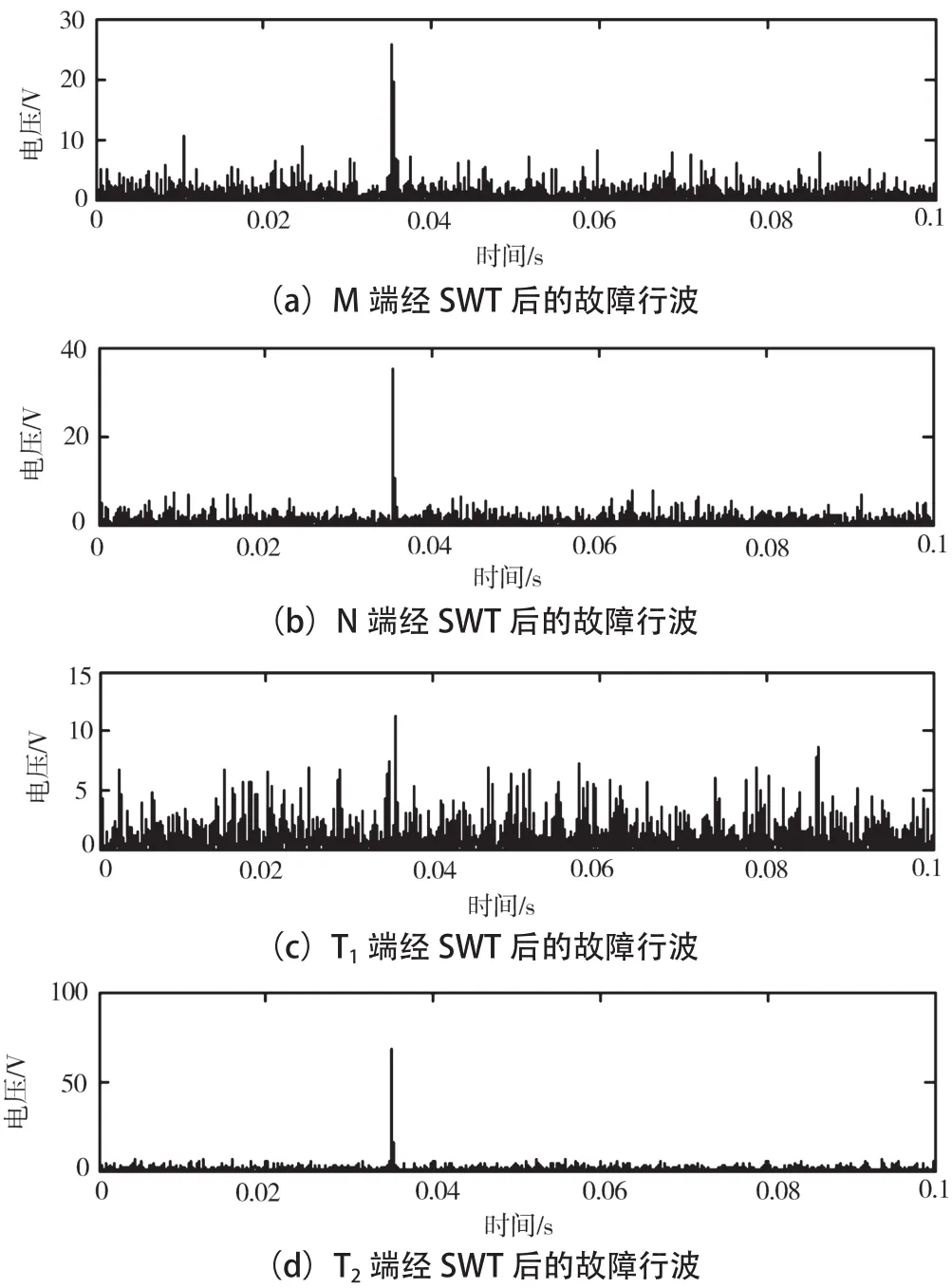
图10 不同端经SWT后的故障行波

4 结 论

本文采用同步压缩小波变换对单相接地故障发生时产生的故障行波进行了时频分析，并得到了最终的测距结果，发现同步压缩小波变换可以较为准确地识别行波波头，并定位故障点，取得了较好的分析效果。

[1] 严 凤，杨奇逊，齐 郑，等.基于行波理论的配电网故障定位方法的研究[J]. 中国电机工程学报，2004，24（9）：37-43.

[2] Montejo L A，Vidot-Vega A L.Synchrosqueezed Wavelet Transform for Frequency and Damping Identification from Noisy Signals[J].Smart Structures and Systems，2012，9（5）：441-459.

[3] 汪祥莉，王 斌，王文波，等.混沌干扰中基于同步挤压小波变换的谐波信号提取方法[J].物理学报，2015，64（10）：100201.

[4] 秦 晅，宋维琪.基于同步压缩变换微地震弱信号提取方法研究[J].石油物探，2016，55（1）：60-66.

[5] 覃 剑，吴成琦.利用小波变换的双端行波测距新方法[J].中国电机工程学报，2000，20（8）：6-10.