一种SVPWM过调制控制策略的分析与仿真
徐鲁辉,崔传辉
(1.比亚迪汽车工业有限公司,广东 深圳 518118;2.聊城大学 东昌学院 机电工程系,山东 聊城 252000)
0 引 言
目前,在直流逆变交流的功率变换过程中普遍使用了三相电压型逆变器。正弦波脉宽调制(SPWM)与空间矢量脉宽调制(SVPWM)两种调制方式,广泛应用于两电平和三电平的逆变控制中。传统SPWM最大相电压峰值是0.5 udc,SVPWM方法在线性调制区内输出最大电压为uUddc。c相比之下,SVPWM调制方式的母线电压利用率高出15.5%,同时六阶梯法有着最高母线电压利用率。
本文提出了一种便于DSP实现的SVPWM过调制策略,无需进行电压判断统一处理两种过调制区的情况,消除了线性调制、过调制与六阶梯波之间的界限,根据实际工况对输出电压幅值进行控制,且实验结果证明了理论分析的正确。
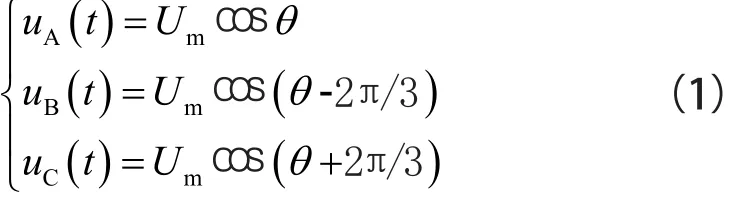
三相电压在空间也是互差120°,则三相电压空间矢量相加的合成空间矢量u(t)可以表示为:
1 SVPWM原理简述
SVPWM是通过三相功率逆变器的六个功率开关元件产生的特定开关模式,从而对三相输出电压进行控制,使得电压空间矢量接近圆轨迹旋转,使电机所产生的实际磁通逼近理想的磁通圆轨迹。与SPWM相比较,SVPWM调制技术使得电机绕组电流波形的谐波成分小,电机转矩脉动降低,旋转磁场更逼近圆形[1-2]。
设三相对称电压瞬时值为uA(t)、uB(t)、uC(t)。它们大小随时间按正弦规律做变化,时间相位互差120°,Um为相电压有效值,f为电源频率,θ=2πft,则:

可见,u(t)是一个旋转的空间矢量,它的幅值为相电压的峰值。空间矢量u(t)在三相坐标轴(a,b,c)上的投影就是对称的三相电压的瞬时值。
三相两电平电压型逆变器的桥臂开关的不同组合,可输出8种状态的电压矢量,其中6个非零矢量(模长均为2/3 udc),2个零矢量,相位互差60°,可将空间分成6个扇区,如图1所示。

图1 基本电压空间矢量的大小和位置
2 过调制控制策略
为了方便分析,本文定义调制比M为[3]:

式中,uref为逆变器输出的空间电压矢量的基波峰6阶梯波调制状态下逆变器输出的电压矢量基波峰值。
当时,M=0.906;当时,M=1。根据调制比大小,可以将电压矢量空间分为线性调制区、过调制I区和过调制II区。
在线性调制区内,指令电压矢量与逆变器输出的电压矢量是一致的,均轨迹为圆形。在过调制区域内,指令电压矢量的轨迹仍是圆形,但逆变器已达到输出极限。此时,指令电压矢量与逆变器输出电压是不同的。
2.1 线性调制区
当电压矢量位于正六边形内切圆内部即urefudc时,电压矢量处于正弦不失真的线性调制区域,电压矢量轨迹均可以由8个基本电压矢量调制实现。此调制区的特点是输出电压在角度和幅值上均可保持连续性。当电压矢量指令达到时,实际输出电压矢量的轨迹沿正六边形的内切圆滑动。在线性调制区内,指令电压矢量与输出电压矢量相等。
以第一扇区为例,电压矢量uref为:

一个调制周期的剩余时间采用零矢量,t0=Tst1-t2。将这段时间均匀分布在一个调制周期的开头、中间和结尾处,形成7段式调制方式。
由三角关系可求出:

2.2 过调制I区
当指令电压处于正六边形内切圆与外接圆之间时,进入了过调制I区。当指令电压矢量的轨迹在正六边形内部时,逆变器输出电压与指令电压一致,可采用线性调制;当指令电压矢量的轨迹超出了正六边形时,逆变器实际无法输出这么大的电压,其幅值会变得比指令电压低,逆变器实际输出的电压会发生畸变。如果继续按照线性调制的方法求解基本矢量作用的时间,则:

逆变器输出的实际电压矢量为指令电压经校正后的电压矢量。当指令电压矢量的轨迹为正六边形外接圆时,达到了过调制I区的极限。
以第一象限为例,uref为电压矢量指令,逆变器输出可实现的电压轨迹为线段AB、曲线BC、线段CD和曲线DE。实际上,此种调制是将电压指令轨迹超出正六边形的部分拉回到正六边形的边上。曲线BC与曲线DE按照线性调制区式(5)计算基本电压矢量的作用时间,线段AB与线段CD按照式(7)确定基本电压矢量作用时间。过调制I区的第一扇区调制如图2所示。

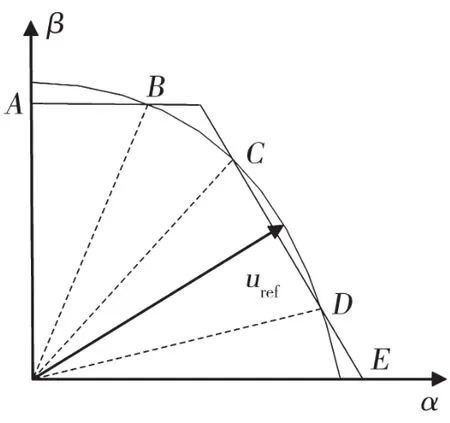
图2 过调制I区第一象限调制示意图
2.3 过调制II区
当指令电压超出正六边形外接圆时,即uref≥ 2 udc3,便进入了过调制II区。指令电压矢量的轨迹在任何位置均超出了正六边形,逆变器实际无法输出这么大的电压,逆变器输出的实际电压矢量为指令电压经校正后的电压矢量。逆变器实际输出的电压会发生畸变,其幅值会变得比指令电压低。如果继续按照线性调制的方法计算基本矢量作用的时间,则:

仍以第一象限为例,uref为电压矢量指令,逆变器输出可实现的电压轨迹为线段AK、点B、线段CD和点E。实际上,此种调制是充分利用六个基本矢量和正六边形的边进一步扩大输出的电压。线段AK与线段CD按照过调制I区式(7)计算基本电压矢量的作用时间,点B与点E按照式(9)确定基本电压矢量作用时间。在基本矢量上作用的时间越长,输出的电压也就越大。当每个基本矢量作用的时间达到1/6周期时,便成了六阶梯波调制。过调制II区的第一扇区调制如图3所示。

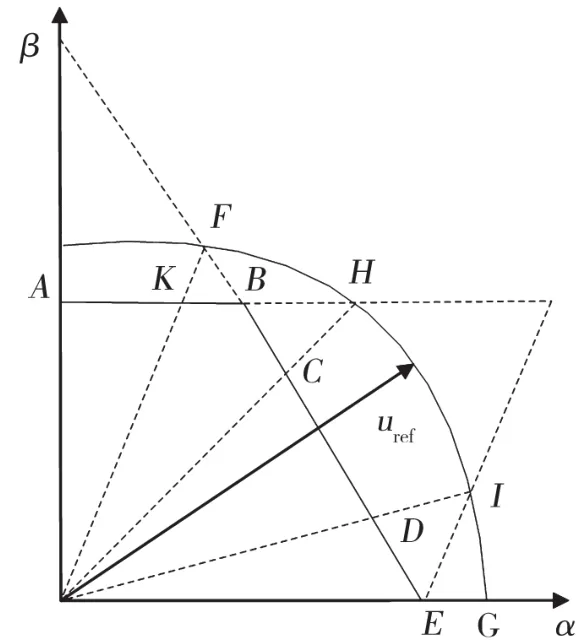
图3 过调制II区第一象限调制示意图
3 过调制算法实现
基于以上对过调制的分析,在SVPWM控制过程中,通过对开关时间的判断进行线性调制、过调制I、过调制II和六脉冲阶梯波处理,从而不必通过电压矢量幅值和调制比来区分过调制区域,将线性调制和过调制统一通过判断逆变器桥臂开关时间来处理。它的控制程序流程如图4所示[4]。
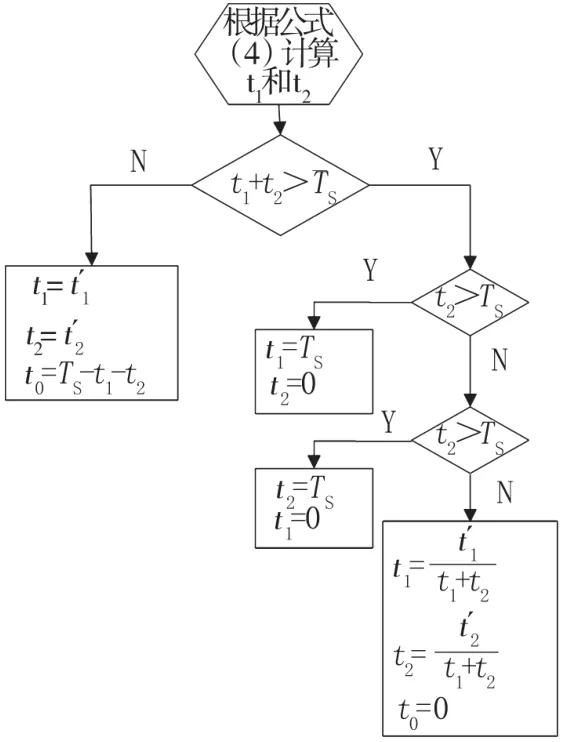
图4 过调制处理控制程序流程图
通过对开关时间的判断,在DSP中可以十分方便得实现上述线性调制、过调制I区和过调制II区的控制。
4 仿真实验
基于以上对SVPWM调制的分析和控制程序流程图,使用simulink、stateflow工具搭建仿真模型,可以获得SVPWM调制各相应阶段的占空比波形,如图5所示。
由仿真占空比波形可知,SVPWM调制的过调制阶段与理论分析相吻合。随着指令电压的增大,SVPWM调制由线性调制区逐渐向过调制区过度。当指令电压足够大时,SVPWM调制变成了六阶梯波控制[5]。

图5 过调制占空比波形图
5 结 论
本文提出了以开关时间作为判断依据的统一处理SVPWM过调制的控制策略,并对其进行了分析推导。设计中不再对电压或调制比进行判断,方便在DSP中在线实施。同时,搭建了仿真实验模型,验证了此策略的有效性和实用性。
[1] 童 军,张 倩,路 尧,等.60°坐标系下三电平逆变器svpwm算法研究[J].微特电机,2018,45(1):20-23.
[2] 张宇翔,张晓荣,张海超,等.一种非对称三电平逆变器svpwm调制方法[J].现代电子技术,2017,24(6): 159-163.
[3] 盛明磊,周 杨,刘 闯.一种基于逻辑判断的SVPWM过调制算法[J].微机电,2017,(11):39-44.
[4] Bae B H,Sul S K.A Novel Dynamic Over-modulation Strategy for Fast Torque Control of High Saliency Ratio AC Motor[C].Industry Applications Conference,2002: 1633-1640.
[5] 张纯江,贲 冰,王晓寰,等.基于三电平SVPWM扇区过渡问题的技术研究[J].电力电子技术,2016,51(4):67-69.

