修正型果蝇优化算法优化SVM的油浸式变压器故障诊断
薛满宇
(北京京能清洁能源电力股份有限公司,北京 100028)
0 引 言
电力系统中,油浸式变压器的作用极为重要,具有分配和运输电能的功能。因此,它的运行状况会直接影响整个电力系统的寿命[1]。所以,科学地诊断油浸式变压器故障对现实实践具有重要的指导意义。在过去的几十年里,一些学者使用诸如人工神经网络[2]、模糊聚类[3]、遗传算法[4]以及小波分析[5]等多种智能优化方法,来诊断变压器故障并取得了一些成就,但是对于算法试验中的数据收集存在一些问题。为了克服这个缺点,支持向量机模型应用而生。它可以用来解决非线性且数量较少的数据,可用于识别维数高的故障诊断,多应用于小样本数据的研究。
在采用SVM模型对变压器进行故障诊断时,要合理选择参数C和g。本文将对果蝇优化算法进行修正后应用于支持向量机,从而获得相关参数的自适应最佳选择,并提高结果的准确度。
1 改进的果蝇优化算法
1.1 果蝇优化算法
果蝇优化算法的简称为FOA,属于智能型算法。该算法的控制参数较少,收敛速度较快,但容易出现“早熟”问题。结合Logistic混沌系统的优点,提出一种基于Logistic混沌系统的修正型FOA,避免FOA局部最优问题。
算法流程如下[6]:
(1)初始化果蝇群体位置,通过propsize表示果蝇群体的大小,Iteration代表最大的迭代次数,该初始位置包含X_begin和Y_begin;
(2)结合式(1)和式(2),确定果蝇个体搜索寻优的方向和距离;
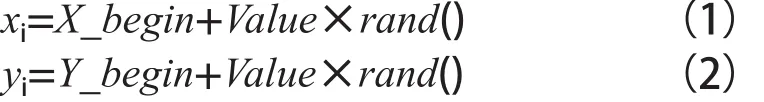
在模型中,用Value表示搜索的距离,单只果蝇的下一时刻的位置分别用xi和yi来代表。

(3)计算单只果蝇到起始点的距离,用di表示:在得知距离的前提下,计算果蝇个体的味道浓度si:

(4)基于函数式(5),计算单只果蝇在此时此位置的味道浓度:

(5)计算果蝇群体的最佳味道浓度和最佳位置,分别用Smellb和(xb,yb)表示;
(6)记录最佳位置,当Smellbest=Smellb、X_begin=xb、Y_begin=yb同时设置后,对这些最佳位置进行寻优迭代操作;
(7)所谓的果蝇最佳位置寻优迭代即将第2步到第5步进行重复,如果味道浓度比前一迭代味道浓度差,那么继续重复;反之,执行下一步骤,停止迭代。
1.2 Logistic混沌系统
已知Logistic混沌系统如式(6)所示[7-8]:
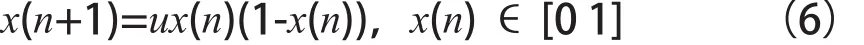
其中,n为迭代次数;u属于控制类参数。当参数u=4时,会形成Logistic混沌状态,该混沌变量Cxi的计算公式为:

其中,Cx(n)i表示混沌映射的第i个混沌变量Cxi在第n步混沌变量之后的值。当Cxi∈[0 1]且Cxi∉{0.25,0.50,0.75}时,系统处于混沌状态。式(7)的优化参数xi∈[aibi],结合式(8)和式(9),同混沌变量当Cxi∈[0 1]进行相互映射变换。其中,表示混沌映射之后的第i个混沌变量Cxi转化成常规变量的值。

1.3 修正型果蝇优化算法
为避免FOA算法局部最优问题,将Logistic混沌理论引入FOA算法,提出一种修正型果蝇优化算法,流程如下:
(1)初始化果蝇位置,处于[0 1]之间,并用行向量zi表示,果蝇群体大小propsize和最大迭代次数Iteration;
(2)zi分量通过式(8)被映射成混沌变量Cz(n)i,Cz(n)i=[0 1];
(3)设置Cz(n)i,然后进行混沌映射;
(4)每个分量通过式(9)实现映射变换,映射为常规变量∈[aibi],并计算适应度选取果蝇种群中最小的,并进行记录,记为
(5)迭代寻优,重复步骤(2)~步骤(4);
(6)若停止条件满足(迭代次数大于最大迭代次数Iteration),则选择最小f i t,使得Smellbest=min(f i t(gen)),此时记录最小所对应的味道浓度Sg;
(7)为了保证参数最优,并将初始迭代值限定在较小的搜索领域内。如果参数大于0,则B∈[0 1];进行反复验证后,设置B=0.25;Sg可以通过Si=Sg+2B×rand()-B进行计算,同时可以求解出f(Si),获取最小值f(Si),并令Bestsmell=min(f(Si));如果 Bestsmell< Smellbest, 则 Smellbest=Bestsmell, 令Sg=Si;
(8)通过重复寻优,不断更新Si,再进行步骤7;
(9)若停止条件满足(迭代次数大于最大迭代次数Iteration),输出Smellbest,P=Sg。
2 IFOA-SVM变压器故障诊断模型
2.1 SVM支持向量机
支持向量机(Support Vector Machine,SVM)是由Vapnik教授提出的一种基于统计学方法的机器学习方法[9]。针对小样本数据分类问题,它具有非常好的效果。假如线性可分样本集(Xi,yi)(i=1,2…,n;X∈Rd,y∈{-1,1}),d维空间中线性判别函数的常规形式为[10-11]:

由式(10)可推导出分类平面方程:

归一化判别函数,调节系数W和b,使得2类所有样本均能满足|g(X)|≥1。此时,分类间隔等于2/||W||,由此将间隔最大化问题转化为解决||W||最小化问题。
最优分类平面的问题转化成最小化优化问题,即[12]:

经过理论推导,将上述问题转化成对偶化问题[13]:

式(13)的矩阵形式为:
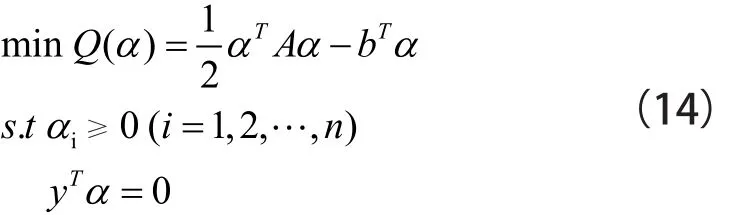
式 中,α=(α1,α2,…,αn)T,b=(1,1,…,1)T,y=(y1,y2,…,yn),Aij=yiyj(xi·xj)。
由式(14)可以推导出最优分类函数为[14]:
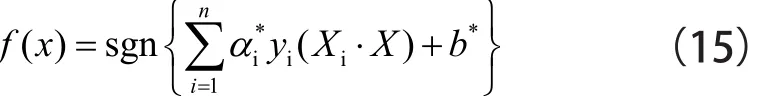
因此,SVM变压器故障诊断模型为:
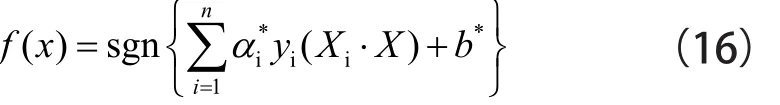
2.2 IFOA-SVM变压器故障诊断模型
由于SVM需要优化的参数为C和g,因此其优化的数学模型为:

通过式(17)的优化,在确保变压器故障诊断准确率最大的情况下,实现参数C和g的自适应选择。
2.3 算法步骤
通过修正果蝇优化算法并应用SVM模型对变压器故障进行诊断的具体算法步骤,如图1所示。第一,将油浸式变压器诊断出的故障数据进行归一。第二,将修正果蝇优化算法的最大迭代次数设为Iteration,用popsize来表示果蝇种群的大小。
第三,将所得到的训练样本数据代入SVM模型,计算果蝇个体的适应度,函数公式详见(17),从而获得果蝇个体的最优值、位置以及相关的群体最优位置、最优值。
第四,改变果蝇当前的位置和搜索方向。
第五,通过公式计算适应度的程度大小,再进行位置和方向的改变。
第六,如果计算得到的gen比maxgen大,说明这个是最优解;如果gen=gen+1,那么将重复步骤4和步骤5。
第七,依据以上计算得到的果蝇群体的最优位置,得知相应的最优参数C和g,从而进一步对变压器故障进行诊断。
3 仿真实验
3.1 优化流程图

图1 基于IFOA_SVM的油浸式变压器故障诊断示意图

图2 优化流程图
搜集油浸式变压器的故障相关数据是首要步骤,其次对已经收集的数据进行分类和处理,基于IFOA算法求得相关参数C和g的最优值,最后将这些值代入SVM诊断故障模型验证结果的准确率。图2为基于IFOA算法优化后的SVM模型的具体流程图。
3.2 实验样本
选择变压器油中含有 H2、CH4、C2H6、C2H4、C2H2等气体的体积含量,构建油浸式变压器故障诊断的训练样本和测试样本。根据样本数据类型,油浸式变压器除了正常状态外,还有六种故障类型,分别是低、中、高温三种温度过热,局部放电,低能以及电弧放电。五种气体分别是H2、CH4、C2H6、C2H4和C2H2。此次验证试验中,需要把这五种气体注入油中溶解,然后测算溶解后的体积含量,代入SVM模型作为输入;SVM的输出则为提到的六种故障模式和正常状态。试验共得到溶解气体后体积含量的数据205组,1~140组为训练集,而剩余的65组数据作为测试集。表1为故障数据样本的具体情况。
3.3 数据预处理
为了降低计算的复杂度,防止在原始数据计算中存在平衡现象,本文选取SVM处理方法,通过归一化方式提高SVM的分类性能:

式(18)中,xi(i=1,2,…,5)属于归一化的样本数据;xmax属于样本数据的最大值;x-i属于所有原始数据的归一化样本结果。

表1 故障数据样本
3.4 实验仿真
通过仿真实验来检验本文算法的结果。本文将试验测得的数据设置为原始数据(初始数据),然后进行交叉验证求得最佳分类准确率,同时获得参数C和g的最佳值。采用IFOA算法对相应的参数进行设置:将参数C和g的范围分别定在(0,100]和(0,1 000],设置200是最大进化代数,20个种群。图3为采用IFOA方法对SVM进行优化得到的寻优适应度情况。可以发现,最优参数值C和g分别是7.188 2和2.989 8,基于IFOA算法优化SVM达到的准确率超过了90%。

图3 基于IFOA算法寻优适应度曲线
将最优参数C和g的值以及训练集数据代入SVM进行检验,然后基于已经建立的SVM油浸式变压器分类模型验证测试集数据,综合使用这些方法对该分类模型的准确度进行检验,最终得出的准确率为95.384 6%。图4较为直观地显示了油浸式变压器的故障分类。
观察图4可发现,除了个别判断错误如第11、14和45样本外,试验诊断故障结果基本符合实际情况。这些误判样本的出现主要有两个原因,一是中高温过热试验得出的数据差距小,使得分类界限不够明确,二是试验中使用的方法或者器具有问题,如SVM分类器自身存在的问题等。
以Grid Search_SVM和FOA-SVM作为基础,对IFOA-SVM和SVM算法得到的结果的准确性进行深入检验,并将验证结果进行对比分析,相关结果如图5、图6和图7以及表2所示。

图4 基于IFOA-SVM测试集分类结果图

图5 基于FOA优化SVM测试集分类结果图

图6 基于网格搜索方法优化SVM测试集分类结果图
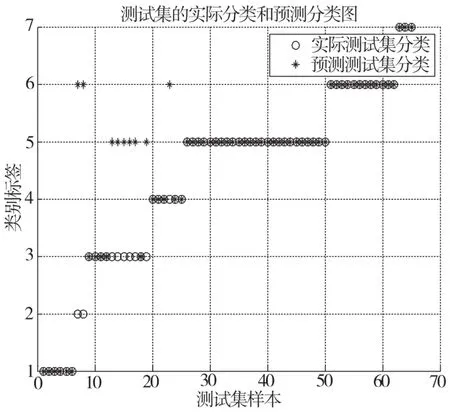
图7 SVM测试集结果分类图

表2 4种方法诊断结果对比
通过观察表2关于IFOA-SVM、FOA-SVM、GRID-SVM以及SVM四种方法得到的结果进行对比发现,前三种方法的结果准确度要比SVM高;FOA并不能有效进行全局寻优而仅限于局部问题,且稳定性不好;IFOA不会陷入局部最优,恰好可以弥补FOA的缺陷;对于FOA-SVM和IFOA-SVM,它们在进行分类检测时准确度相差较小;对于GRID-SVM方法,在网格搜索时需要消耗较长的时间,搜索速度较慢、搜索范围需要先置等,尽管期分类准确率可以达到很高,但是很难保证结果真正有效和准确。综上所述,SVM的监测结果准确度在同类四种方法中最低,不能用于诊断浸式变压器故障。
4 结 论
为了更好地对样本数量较少的油浸式变压器进行检测和诊断,以IFOA为基础并进行修正和优化SVM的方法IFOA-SVM被提出,并受到重用。该方法引入了惩罚因子和核函数参数来对油浸式变压器进行故障检测,分别用C和g来表示。仿真实验的最终结果表明,相较于Grid Search-SVM、FOA-SVM和SVM诊断油浸式变压器故障,IFOA-SVM的诊断结果较为准确。
[1] Gu W,Lv Z,Hao M.Change Detection Method for Remote Sensing Images Based on an Improved Markov Random Field[J].Multimedia Tools and Applications,2015:1-16.
[2] Chen Z,Huang W,Lv Z.Towards a Face Recognition Method Based on Uncorrelated Discriminant Sparse Preserving Projection[J].Multimedia Tools and Applications,2015:1-15.
[3] Jiang D,Ying X,Han Y,et al.Collaborative Multihop Routing in Cognitive Wireless Networks[J].Wireless Personal Communications,2015:1-23.
[4] Lv Z,Tek A,Da Silva F,et al.Game on,Sciencehow Video Game Technology May Help Biologists Tackle Visualization Challenges[J].PloS one,2013,8 (3):57990.
[5] Wen-Tsao P.A New Fruit Fly Optimization Algorithm:Taking the Financial Distressmodel as an Example[J].Knowledge-Based Systems,2012,(26):69-74.
[6] Gu W,Lv Z,Hao M.Change Detection Method for Remote Sensing Images Based on an Improved Markov Random Field[J].Multimedia Tools and Applications,2015:1-16.
[7] 丁世飞,齐丙娟,谭红艳.支持向量机理论与算法研究综述[J].电子科技大学学报,2011,40(1):2-10.
[8] 陈 亮.改进自适应差分进化算法及其应用研究[D].上海:东华大学,2012.
[9] 章 萌,章卫国,孙 勇.多目标强度Pareto混沌差分进化算法[J].控制与决策,2012,27(1):41-47.
[10] 刘志刚,李德仁,秦前清,等.支持向量机在多类分类问中的推广[J].计算机工程与应用,2004,16(7):96-100.
[11] Wang K,Zhou X,Li T,et al.Optimizing Load Balancing and Data-locality with Data-aware Scheduling[C].Big Data,2014 IEEE International Conference on,2014:119-128.
[12] Lin Y,Yang J,Lv Z,et al.A Self-Assessment Stereo Capture Model Applicable to the Internet of Things[J].Sensors,2015,15(8):20925-20944.
[13] Yang J,He S,Lin Y,et al.Multimedia Cloud Transmission and Storage System Based on Internet of Things[J].Multimedia Tools and Applications,2015:1-16.
[14] Sheng G,Dang S,Hossain N,et al.Modeling of Mobile Communication Systems by Electromagnetic Theory in the Direct and Single Reflected Propagation Scenario[M].Springer Berlin Heidelberg,2015:280-290.

