基于反推算法的6相感应电动机新型矢量控制

包广清, 张继龙, 张小龙, 李小东

(1. 兰州理工大学 电气工程与信息工程学院, 甘肃 兰州 730050; 2. 兰州理工大学 甘肃省工业工程先进控制重点实验室, 甘肃 兰州 730050; 3. 兰州理工大学 电气与控制工程国家级试验教学示范中心, 甘肃 兰州 730050; 4. 甘肃省定西市渭源县新寨镇 康家山小学, 甘肃 定西 748211)

相比于三相调速系统,多相调速系统具于低压下实现大功率输出、转矩性能平稳、可靠性高、转子谐波损耗小、动静态性能好等优势,并且可在缺相情况下通过调整控制策略继续运行[1-2].因此,特别在电动汽车、航空航天、矿井提升、机车牵引、舰船推进等应用场合的研究日趋广泛[3-4].传统的多相感应电动机矢量控制采用控制简单、适用性好的PI控制器,但PI控制器基于稳态模型,忽略了系统的瞬态特性,因而具有动态响应慢的缺点,同时多相感应电动机是一个非线性、高阶、强耦合、多变量的系统,因此非线性的PI控制器参数通常难以整定.

反推控制方法[5]是针对不确定性系统的一种非线性算法,特别适合于多相感应电动机这样的非线性系统.该方法通过给系统引入虚拟变量,设计出满足要求的虚拟控制,最终设计出真正的控制规律.目前该方法已用于永磁同步电动机速度跟踪控制中,具有优良的鲁棒性[6-7].文献[8]选取转速和电流为控制量,设计了反推控制器,实现了永磁同步电动机转速跟踪控制.反推控制方案目前已被用于三相永磁同步电动机控制,但是其在多相电动机矢量控制中未有应用[9-10].因此,文中将反推控制引入6相感应电动机矢量控制中,用于改进传统矢量控制的性能.

文中建立电动机数学模型并以减小定子谐波电流为目的确定SVPWM控制方案;将反推控制与矢量控制相结合,根据非线性反推控制方法设计速度反推控制器、磁链反推控制器和转矩反推控制器;在此基础上,用MATLAB/Simulink建立该系统的仿真模型并对所提出的方法进行分析验证.

1 6相感应电动机模型

为了改进电动机性能,文中研究6相感应电动机定子的绕组是2套独立互差30°电角度且中心点隔离的对称三相绕组,其转子采用标准鼠笼型结构.采用这种绕组的电动机能够完全消除危害最为严重的谐波磁动势和6次谐波转矩脉动[11].

自然坐标系下的电动机模型是高阶、非线性、强耦合的,为了便于控制,将六维的电动机模型通过空间矢量解耦矩阵T6分解成为机电能量转换的xO1y子空间和与其垂直的μO2ν,o1O3o2两个谐波子空间[12].再利用Park变换将电动机模型变化到dOq旋转坐标系下,经整理得电动机定转子磁链方程为

(1)

式中:Ls=Lls+3Lms;Lr=Llr+3Lms;Lm=3Lms;Lls,Llr分别为定转子漏感;Lms为定子间互感.

电压方程为

(2)

式中:p为微分算子;ω为电动机转子角速度;ω1为同步角速度.

基于转子磁链定向的矢量控制是将转子磁链定向在d轴上,这样转子磁链在q轴的分量为0,转子电压为0(转子为鼠笼型结构).为了实现6相感应电动机的反推矢量控制,由上述方程可推出6相电动机在mOt同步旋转坐标系下的状态方程为

(3)

mOt坐标系的旋转角速度为

(4)

mOt坐标系的电磁转矩为

(5)

2 SVPWM算法

6相电动机定子绕组结构导致μO2ν子空间谐波电流较大,因此6相SVPWM核心宗旨就是综合各个空间内的电压矢量去满足电动机控制要求,尽可能减小谐波电流,使得μO2ν子空间的伏秒平衡并让平均合成电压为0,实现磁链的快速跟踪.6相电压源逆变器共有64种转换开关状态,不同转换开关状态K={KC2,KC1,KB2,KB1,KA2,KA1}相对应的64种空间电压矢量经过矢量解耦矩阵T6投影到xO1y，μO2ν，o1O3o2子空间如图1所示.由于电动机定子绕组中性点隔离,此时投影于o1O3o2子空间电压矢量幅值为0.

在xO1y子空间上,3,7,15,14,12,28,60,56,48,49,51,35这12个空间电压矢量的幅值最大.选择其中任意3个相邻的电压矢量,当这3个相邻的电压矢量的作用时间符合特定比例时,合成的新虚拟电压平衡矢量在μO2ν子空间的伏秒特性为0,如图2所示.

图2 12个新虚拟电压平衡矢量及其扇区分布

例如选取xO1y平面上的相邻电压矢量3,7,15合成新虚拟电压平衡矢量U2vir,合成表达式为

(6)

3 系统控制器设计

3.1 6相感应电动机反推控制器设计

对于6相感应电动机系统,假设系统的控制目标是电动机转速跟踪,定义转速跟踪误差eω为

eω=ω*-ω.

(7)

选取eω为状态变量构成子系统,根据式(7)对转速跟踪误差求导得出

(8)

为了使转速跟踪误差趋于0,选取电磁转矩和磁链为虚拟控制函数,对于子系统式(8)构造Lyapunov函数为

(9)

对式(9)求导得出

(10)

为了使式(10)满足dV1/dt<0,选取给定转矩和磁链为

(11)

当kω>0时,则式(10)为

(12)

因此满足控制式(11),即可实现转速全局的渐近跟踪稳定.为了控制电磁转矩和磁链,选取转矩误差和磁链误差为虚拟误差变量为

(13)

由eω,eTe,eψ可以构成新的控制系统,对式(13)中的转矩误差和磁链误差求导得出

(14)

(15)

令

(16)

因此式(14)-(15)可写为

(17)

(18)

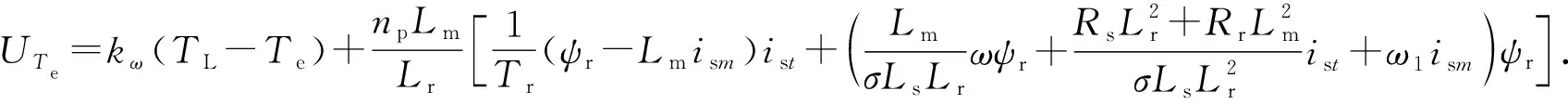
对系统构造新的Lyapunov函数为

(19)

对式(19)求导得出

(20)

由于式(18)中含有实际控制量ust,而式(17)中未含实际控制量usm,因此可定义新的虚拟变量函数为

s=Lmism.

(21)

由式(16)-(17)得s*=ψr+kψeψTr,则新的虚拟误差变量为

es=s*-s.

(22)

对新的虚拟误差变量求导得出

(23)

对于整个系统构造新的Lyapunov函数为

(24)

令

(25)

对式(24)求导得出

(26)

为了使式(26)满足dV3/dt<0,由式(18),(23),(25)设计实际控制量usm,ust为

(27)

(28)

将式(27),(28)代入式(26)可得

(29)

式中kTe>0,ks>0,kψ>0.

则控制式(27),(28)可以使得6相感应电动机系统不但达到转速渐近跟踪的效果,同时使磁链和电磁转矩得到准确地控制,使得系统全局具有响应速度快和指数稳定的特点.

3.2 系统稳定性证明

(30)

由于V3有界,因此根据Barbalat推论,可得出

(31)

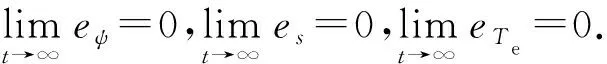
4 6相系统仿真验证与分析

基于反推算法的6相感应电动机新型矢量控制系统结构框图如图3所示.

图3 基于反推算法的6相感应电动机新型矢量控制系统

转速反推控制器由式(11)实现,磁链和转矩反推控制器由式(27),(28)实现.此系统调节参数仅4个,与一般的PI控制(假设速度控制器、磁链控制器、转矩控制器、电流控制器都选择PI设计,则调节参数有10个)相比较,反推控制的调节参数显著减少.

6相感应电动机的主要参数如下:额定功率PN=2 kW;额定电压UN=120 V;定子电阻Rs=0.85 Ω;转子电阻Rr=0.85 Ω;定子电感Ls=0.274 H;转子电感Lr=0.274 H;定转子互感Lm=0.270 H;极对数np=3;转动惯量J=0.1 kg·m2.系统开关频率为5 kHz,假定转速给定值为500 r·min-1,磁链给定值为0.5 Wb.电动机在0.3 s加上15 N·m的负载转矩,0.5 s卸载.

Backstepping控制器的参数设置如下:kω=1 000;kTe=50;kψ=600;ks=500.

Backstepping控制的仿真结果见图4,传统的PI控制仿真结果见图5.

由图4a,5a可见反推控制的启动响应速度比PI控制快(PI控制系统到达给定转速的响应时间约为0.13 s,而反推控制系统约为0.04 s);由图4b,5b,4c,5c可见反推控制的电动机转矩脉动小(传统PI控制系统转矩波动为1.2 N·m,反推控制系统为0.6 N·m)、响应速度快、无时延现象,电动机加/卸载时转速超调或者跌落值均很小;由图4d,5d,4e,5e可见反推控制的电动机电流波形更接近正弦,转子磁链波形正弦度更好且幅值更接近于设定值、无超调.

图4 反推控制仿真图

图5 PI控制仿真图

仿真结果表明,系统Backstepping控制的速度和转矩波动小、调节时间短,并且具有良好的速度和磁链跟踪效果,同时保证系统具有良好的动静态性能.与传统的PI控制相比较,Backstepping控制加快了系统的跟踪速度,同时在系统突加负载和卸载时降低了对速度的影响,其电流变化平稳,基本没有调节过程,表明系统对转矩扰动有明显的抑制作用,并且能够有效地减少控制参数的数量.因此所提出的反推控制策略能够满足调速系统的性能要求.

5 结 论

文中针对6相感应电动机传统矢量控制存在的问题,提出了一种基于反推控制算法的6相感应电动机新型矢量控制方法,并对该方法进行了仿真分析研究.该方案具有参数便于调节、响应速度快、控制精度高、动静态性能良好、能够保证系统的全局渐近稳定,控制效果更具有明显的优越性.与传统的PI控制进行了对比分析,结果表明这种方法能够改善电动机转矩脉动、定子电流波形,使系统具有良好的鲁棒性,验证了系统设计的有效性.

参考文献(References)

[ 1 ] ABDEL-KHALIK A S, MASSOUD A M, AHMED S. A senior project-based multiphase motor drive system development[J]. IEEE Transactions on Education, 2016, 59(4): 307-318.

[ 2 ] PANDIT J K, AWARE M V, NEMADE R V, et al. Direct torque control scheme for a six-phase induction motor with reduced torque ripple[J]. IEEE Transactions on Power Electronics, 2017, 32(9): 7118-7129.

[ 3 ] 耿乙文, 鲍宇, 王昊, 等. 六相感应电机直接转矩及容错控制[J].中国电机工程学报, 2016,36(21): 5947-5956.

GENG Y W, BAO Y, WANG H, et al. Direct torque and fault tolerant control for six-phase induction motor[J]. Proceedings of the CSEE, 2016,36(21):5947-5956. (in Chinese)

[ 4 ] BIANCHI N, FORNASIERO E, BOLOGNANI S. Thermal analysis of a five-phase motor under faulty operations [J]. IEEE Transactions on Industry Applications, 2013, 49(4): 1531-1538.

[ 5 ] AMEID T, MENACER A, TALHAOUI H, et al. Sensorless speed estimation and backstepping control of induction motor drive using model reference adaptive system[C]∥Proceedings of the 5th International Confe-rence on Electrical Engineering. New York: IEEE, 2017.

[ 6 ] 徐艳平, 雷亚洲, 马灵芝, 等. 基于反推控制的永磁同步电机新型直接转矩控制方法[J]. 电工技术学报, 2015, 30(10): 83-89.

XU Y P, LEI Y Z, MA L Z, et al. A novel direct torque control of permanent magnet synchronous motors based on backstepping control [J]. Transactions of China Electrotechnical Society, 2015, 30(10): 83-89. (in Chinese)

[ 7 ] TING C S, CHANG Y N, SHI B W, et al. Adaptive backstepping control for permanent magnet linear synchronous motor servo drive[J]. IET Electric Power Applications, 2015, 9(3): 265-279.

[ 8 ] 刘栋良, 郑谢辉, 崔丽丽. 无速度传感器永磁同步电机反推控制[J]. 电工技术学报, 2011, 26(9): 67-72.

LIU D L, ZHENG X H, CUI L L. Backstepping control of speed sensorless permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society,2011,26(9):67-72. (in Chinese)

[ 9 ] RASTEGAR FATEMI S M J, ABJADI N R, SOLTANI J, et al. Speed sensorless control of a six-phase induction motor drive using backstepping control[J].IET Power Electronics,2014,7(1):114-123.

[10] 谢颖, 葛红岩, 连国一. 考虑磁场饱和的电动汽车用永磁电机控制仿真[J]. 江苏大学学报(自然科学版), 2016, 37(1):60-66.

XIE Y,GE H Y,LIAN G Y. Simulation of permanent magnet synchronous motor vector control for electric vehicles considering magnetic saturation[J]. Journal of Jiangsu University (Natural Science Edition), 2016, 37(1):60-66. (in Chinese)

[11] 耿乙文, 周勤奋, 鲍宇, 等. 基于叠加复调节器的双三相感应电机控制系统[J]. 中国电机工程学报, 2015, 35(13): 3426-3435.

GENG Y W, ZHOU Q F, BAO Y, et al. The control system for dual three-phase induction motor based on a superposition of complex regulators[J]. Proceedings of the CSEE, 2015, 35(13): 3426-3435. (in Chinese)

[12] 盛爽, 陆海峰, 瞿文龙, 等. 双三相感应电机谐波平面电压注入法在线辨识定子电阻和漏感策略[J]. 中国电机工程学报, 2014, 34(6): 872-881.

SHENG S, LU H F, QU W L, et al. The stator resis-tance and leakage inductance on-line identification strategy of dual three-phase induction motors by voltage vector injection in harmonic subspace[J]. Proceedings of the CSEE, 2014, 34(6): 872-881. (in Chinese)