基于二阶Thevenin模型的锂电池建模仿真

闫回想, 甘小燕, 武鸿辉, 刘岸晖

(1. 武汉理工大学 现代汽车零部件技术湖北省重点实验室, 湖北 武汉 430070; 2. 武汉理工大学 汽车零部件技术湖北省协同创新中心, 湖北 武汉 430070)

电池在工作中由于受到外部环境及其自身因素的影响往往表现出高度非线性的外在特性,使得建立高精度电池模型成为电动汽车系统建模过程中的难点之一.

为了建立高精度的电池模型,笔者通过对电池模型的介绍,综合考虑建模难度和仿真精度后,选取二阶Thevenin模型为研究对象,通过HPPC(hybrid pulse power characteristic)试验对模型参数进行辨识,在Matlab/Simulink中建立电池模型,对参数有效性进行仿真验证,通过仿真结果和试验结果的拟合程度以及误差分析,证明模型能够以较高精确反映电池外部动态特性.

1 电池模型介绍

常见的电池模型包括数学模型、电化学模型、耦合模型、神经网络模型以及等效电路模型[1-2].

机理模型和经验模型是比较常用的数学模型,前者一般是通过合理的假设,运用基本的传递和反应方程进行理论分析,计算过程较复杂;后者是建立在大量试验基础上,常用作单电池性能的简单模型.

电化学模型是根据电池内部反应原理建立的模型,包括单粒子模型[3-4]和一维模型[5].在单粒子模型的基础上,一维电化学模型基于浓溶液理论与多孔电极理论,添加了液相浓度、液相电势以及荷电状态对电极扩散系数的影响,以此来仿真电池内部行为.

耦合模型是综合不同模型的优点来实现电池性能仿真.如电化学-热耦合模型将电化学模型和热模型进行耦合.电化学模型描述电池内部反应过程,热模型描述电池热状态.前者为后者提供电池在不同状态下的生热速率,后者为前者提供实时的电池反应温度[6].

人工神经网络模型是由许多简单并行工作的处理单元构成的系统,其功能取决于网络的结构、连接强度及各单元的处理方式.该模型具有高度的并行结构和处理能力,具有任意非线性映射能力,可以拟合高度非线性数据.文献[7]采用神经网络算法成功地建立了锂离子电池模型,并且准确地预测了电池组的剩余容量.

电池作为储能装置可简化为固定电压源与内阻的串联.基于电池的动态特性及工作原理,通过使用电阻、电容和电压源构成电路网路来建立等效电路模型.

2 锂电池基本性能试验

以18650NCM锂电池为试验对象,其基本参数:标称容量为2 500 mA·h;标称电压为3.7 V; 最大充电电流为1.0 C;最大持续放电电流为5.0 C;充电截止电压为4.2 V;放电截止电压为2.5 V.

试验设备主要包括Neware BTS4000电池测试系统、多功能夹具、恒温箱和控制电脑等.设备连接如图1所示.

图1 试验设备连接示意图

2.1 恒流恒压充电试验

首先以恒定电流(0.3 C)对电池充电,当电压到达截止电压(4.2 V)时,转为恒压充电,直至充电电流减小到预设截止电流(0.13 A)充电完成.充电过程中电压和电流变化曲线如图2所示.

图2 恒流恒压充电曲线

2.2 不同倍率放电试验

温箱温度设为30 ℃,放电截止电压设为2.5 V,分别以0.5,1.0,2.0,3.0 C对电池进行放电.试验结果如图3所示.

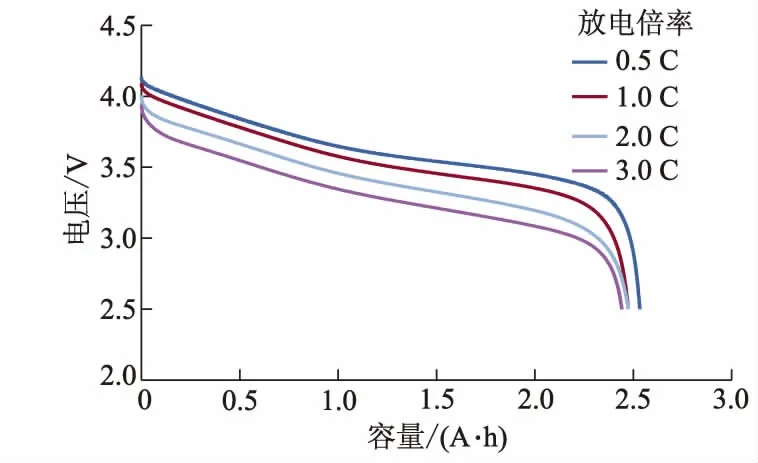
图3 温箱温度为30 ℃时,电池不同倍率放电曲线

从图3可以看出,不同倍率放电过程中电池电压曲线大致可分为3个阶段: ① 放电初始阶段电压瞬时下降,放电倍率越大下降越大; ② 电池电压进入一个缓慢变化的时期,这个时期称为电池放电电压平台区,放电倍率越小,平台区电压越高; ③ 电池放电即将结束时,电池负载电压曲线出现“拐点”,然后电压开始急剧下降至终止电压,“拐点”随着放电倍率的增大会提前出现,并且“拐点”处电压也会随着放电倍率增大而降低.

2.3 HPPC放电试验

测试前先计算该放电倍率的放电周期(每循环深度放电时间=该倍率放电总时间/循环次数),此次试验每次循环使SOC值下降0.1,共循环10次.HPPC具体测试步骤参考文献[8].HPPC放电试验电压电流曲线如图4所示.

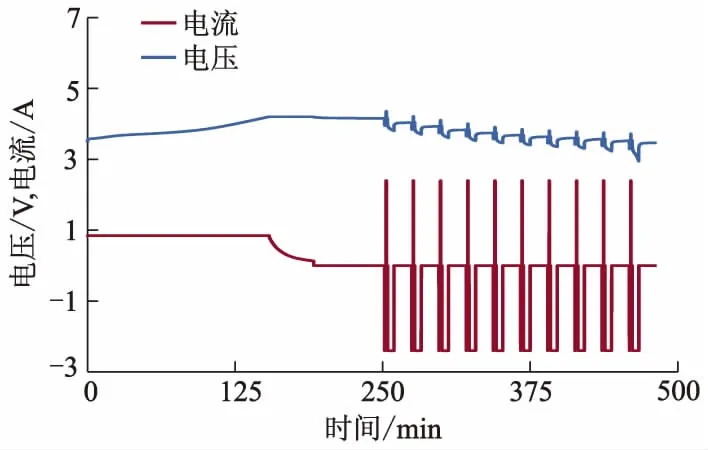
图4 HPPC放电试验曲线

3 模型参数辨识

二阶Thevenin模型如图5所示,需要辨识的参数包括Uo,R0,R1,C1,R2和C2.

通过HPPC放电试验对参数进行辨识,任意选取其中一次循环脉冲试验曲线来说明参数辨识的原理及过程,如图6所示.

图5 二阶Thevenin模型

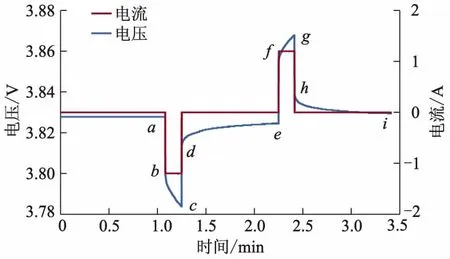
图6 一次循环脉冲电压、电流曲线

a点之前电池处于长时间的搁置状态,电流为0,电池内部极化效应逐渐减弱,当到达a点时内部极化效应可以忽略不计;ab段是以0.5 C放电时电压的瞬间变化;bc段是放电10 s过程中的电压变化;cd段是放电结束时电压瞬间变化;de段是电池放电结束后搁置期间的电压变化.充电过程与放电过程类似.i点之后对电池进行放电使SOC值下降0.1,为下一个SOC点脉冲试验做准备.

3.1 开路电压Uo辨识

采用文献[9]提出的开路电压辨识方法.在每次脉冲充放电后搁置过程中,即图6中de段和hi段,此时电流为0,极化电压逐渐减小;e点和i点可认为极化电压为0,可以取e点与i点电压作为开路电压.为了进一步减小极化电压的影响,取e点和i点电压的平均值作为对应SOC点的开路电压.表1为30 ℃时0.5 C放电HPPC试验辨识的开路电压值.

表1 开路电压参数表

3.2 欧姆内阻R0辨识

图6中ab,cd,ef以及gh段都是由于欧姆内阻引起的电压瞬变,根据欧姆定律可计算出欧姆内阻.同样为了减小极化效应对R0参数辨识的影响,取放电脉冲和充电脉冲开始时的瞬间电压变化与相应充放电电流比值的平均值为R0.温度为30 ℃时放电电流为0.5 C,HPPC试验辨识的欧姆内阻R0如表2所示.

表2 欧姆内阻参数表

3.3 R1,R2,C1,C2参数辨识

由图5可得

UL=Uo+IR0+U1+U2,

(1)

(2)

由式(2)可得

(3)

(4)

已知时间常数τ=RC,τ反映了电池充放电后到达稳态的快慢,要对RC环节中电阻与电容进行辨识,首先要求出τ.结合时间常数表达式,求解式(3),(4)可得

(5)

(6)

式中:U1(0),U2(0)为在每次脉冲结束瞬间电容两端初始电压;t为极化效应响应时间.

先对放电方向进行参数辨识,在图6中de段为放电脉冲结束后搁置60 s的电压变化曲线,电流输入为0,此时可看作是RC环节零输入状态时响应,端电压可表示为

(7)

根据式(7),在Matlab中使用cftool对电池脉冲放电后搁置60 s,电压变化曲线进行拟合,可以求得U1(0),U2(0),τ1,τ2.

对于bc段,b点之前电池已被搁置很久,其内部极化效应基本消失,可认为极化电压为0,因而bc段看作是RC环节的零状态响应.极化电容两端电压为

(8)

(9)

从c点到d点的瞬间电池极化电压基本不变,由此可得

(10)

(11)

式中tk为b点到c点放电脉冲的加载时间,为10 s.

将已求得的U1(0),U2(0),τ1,τ2代入式(10),(11)可求得R1和R2,再根据时间常数表达式求出C1与C2,放电方向下,2个RC环节辨识参数如表3所示.

表3 放电方向下电阻和电容值

2个RC环节充电方向所辨识的电阻和电容值如表4所示.

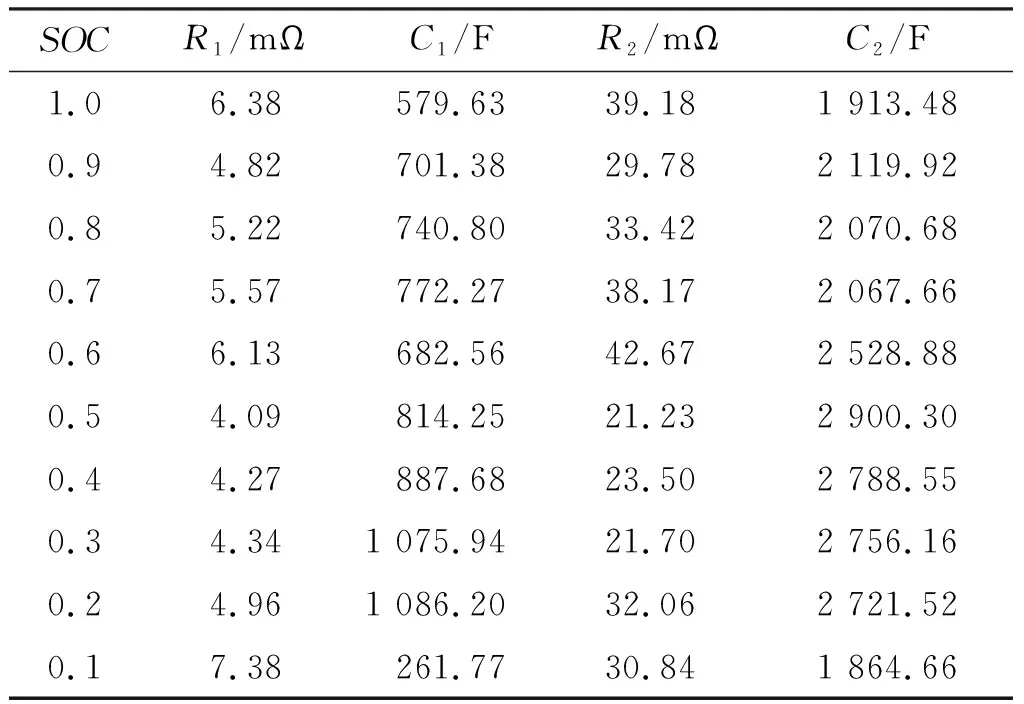
表4 充电方向下电阻和电容值

4 电池模型建模与仿真

由式(1),(5),(6)在Matlab/Simulink中搭建电池模型,但式(1),(5),(6)这3个数学表达式都是连续的,而试验数据采集时间间隔为0.1 s,因此需要对上述的电路状态关系式进行离散化[10],离散化后的结果为

(12)

式中:It为t时刻电池的充放电电流,设定放电时为负值;UL(t)为t时刻电池的端电压;U1(t+1),U2(t+1)分别为t+1时刻R1C1和R2C2这2个RC环节两端的电压;Δt为采样周期,试验中的数据采集周期为0.1 s.

4.1 HPPC放电试验仿真

在15 ℃和30 ℃下,对电池进行HPPC放电试验,放电电流为0.5 C,试验与仿真结果对比如图7所示.

图7 HPPC放电试验值与仿真值对比曲线

SOC=1-t1/t0，t1为当前放电时长，t0为放电总时间.从图7可以看出：SOC为1.0～0.2(图7a放电时间为0～600 min或图7b放电时间为0～232 min)时，仿真值与试验值重合度较好；当SOC为0.2～0(图7a放电时间为600～750 min或图7b放电时间为232～290 min)时，重合度有所下降.试验与仿真的误差曲线如图8所示，在15 ℃和30 ℃时，SOC在1.0～0.2时，误差分别保持在0.05 V和0.04 V以内；当SOC在0.2～0时误差显著增加，误差分别增加到0.24 V和0.12 V.推测其主要原因是在HPPC放电测试时，SOC值采集点间隔为0.1，而SOC值在0.2～0时电池内阻变化又非常大,根据试验数据采集点，仅辨识出SOC值在0.1和0.2处的电池内阻，导致在后期的曲线拟合中不能以较高精度拟合出SOC值在0.2～0时的实际内阻变化，因此在后期的仿真中产生较大的误差.

图8 HPPC放电试验端电压误差曲线

4.2 恒流放电测试仿真

在15 ℃和30 ℃条件下,对锂电池进行恒流放电测试,放电电流设为0.5 C,试验测试结果与仿真结果对比如图9所示.

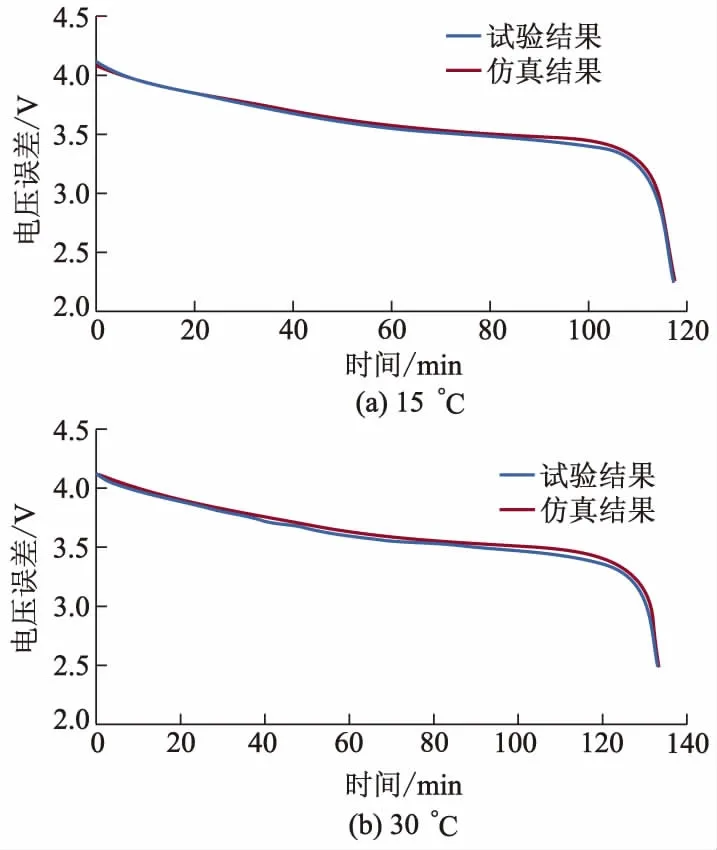
图9 恒流放电试验值与仿真值对比曲线

从图9可以看出：在2种不同温度条件下，二阶Thevenin模型对电池恒流放电工况仿真具有较高的精度.恒流放电试验与仿真的误差曲线如图10所示，当SOC值在1.0～0.2(图10a放电时间为0～95 min或图10b放电时间为0～108 min)时，仿真误差基本保持在0.04 V以内；当SOC值在0.2～0(图10a放电时间为95～118 min或图10b放电时间为108～135 min)时，随着SOC值的减小，误差显著增大，最大误差为0.09 V.

图10 恒流放电端电压误差曲线

5 结 论

二阶Thevenin模型能够对锂电池在不同条件下的外特性曲线以较高精度进行仿真,该模型对于研究锂电池动态特性和电池系统设计具有重要意义.为了进一步提高该模型的仿真精度,可以进行如下改进: ① HPPC试验中减小SOC的间隔,采集更多的SOC点; ② 对参数进行多项式拟合时,尽可能使用更高阶的多项式,提高拟合精度; ③ 对数据进行处理时,要把握好数据的精度; ④ 降低试验测试过程中环境因素对试验结果的不利影响.

参考文献(References)

[ 1 ] 陈全世,林成涛.电动汽车用电池性能模型研究综述[J].汽车技术,2005(3):1-5.

CHEN Q S,LIN C T.Summarization of studies on perfor-mance models of batteries for electric vehicle [J].Automobile Technology,2005(3):1-5.(in Chinese)

[ 2 ] 袁翔,张毅.电动汽车用动力电池模型研究进展[J].公路与汽运,2014(2):1-7.

YUAN X,ZHANG Y.Research progress of power battery model for electric vehicle[J].Highways & Automotive Applications,2014(2):1-7.(in Chinese)

[ 3 ] SANTHANAGOPALAN S,GUO Q Z,RAMADASS P,et al.Review of models for predicting the cycling perfor-mance of lithium ion batteries[J].Journal of Power Sources,2006,156(2):620-628.

[ 4 ] 黄亮,李建远.基于单粒子模型与偏微分方程的锂离子电池建模与故障监测[J].物理学报,2015,64(10):1-6.

HUANG L,LI J Y.Modeling and fault monitoring of Li-ion battery based on single particle model and partial differential equation[J].Acta Physics Sinica,2015,64(10):1-6.(in Chinese)

[ 5 ] ALEBERTUS P,CHRISTENSEN J,NEWMAN J.Experiments on and modeling of positive electrodes with multiple active materials for lithium-ion batteries[J].Journal of the Electrochemical Society,2009,156(7):606-608.

[ 6 ] 汤依伟.基于电化学-热耦合模型的锂离子动力电池放电行为研究[D].长沙:中南大学,2013.

[ 7 ] SHEN W X,CHEN C C,LO E W C,et al.A new battery available capacity indicator for electric vehicles using neural network[J].Energy Conversion and Management,2002,43(6):817-826.

[ 8 ] 林春景,李斌,常国锋,等.不同温度下磷酸铁锂电池内阻特性实验研究[J].电源技术,2015,39(1):22-25.

LIN C J,LI B,CHANG G F,et al. Experimental study on internal resistance of LiFePO4batteries under diffe-rent ambient temperatures[J].Chinese Journal of Power Sources,2015,39(1):22-25.(in Chinese)

[ 9 ] ABU-SHARKH S, DOERFFEL D. Rapid test and non-linear model characterization of solid-state lithium-ion batteries[J]. Journal of Power Sources, 2004, 130(2): 266-274.

[10] 欧少端,杨晓力,周乃君.基于PNGV电容模型的LiFePO4电池性能仿真与实验[J].电源技术,2013, 37(7):1133-1135.

OU S D,YANG X L,ZHOU N J.Simulation and experiment study on PNGV capacitance model of LiFePO4power battery for vehicle[J]. Chinese Journal of Power Sources,2013,37(7):1133-1135.(in Chinese)