基于Smith预估器的自适应模糊PID在电缆线径控制系统中的应用

周克良，王荡荡,韩李珂

(江西理工大学 a.电气工程与自动化学院; b.机电工程学院， 江西 赣州 341000)

电缆护套生产线的主要功能是挤出一层绝缘材料包裹在芯线外层，对电缆起保护作用[1]。传统的护套线径控制系统采用反馈控制，通过测径仪反馈的实际外径值与工艺要求的设定值比较得到线径偏差，然后经过控制器的PID运算产生控制信号来控制挤塑机的出料速度或牵引机的牵引速度，进而来控制产品的线径[2]。尽管这种经典的控制方式在结构上比较简单，并且稳定性较好，但挤塑机系统本身是一个复杂的大滞后系统，又具有时变性、非线性等特点，传统PID控制表现出对系统参数变化的鲁棒性比较差、抗负载扰动能力不太强等缺点，不能满足当今电缆行业的要求。针对此，国内外专家学者将智能控制算法引入各行业领域解决实际问题。武斌等[3]实践探索了模糊控制的工程应用。周克良等[4]提出了可变论域的模糊PID控制策略。王春艳[5]、张连会[6]、曾庆良等[7]将模糊控制与Smith预估补偿结合引入温度控制系统。本文采用的自适应模糊PID(AFPID)不同于常规模糊控制方法之处在于控制器的调整通过可调参数实现，相比调整模糊规则或隶属度函数更灵活简单。本文同时引入Smith预估补偿环节来改善滞后时间的不良影响，并针对Smith预估器对模型精度要求太高这一不足，提出了改进的Smith预估控制方案，改善了系统参数变化时滞后环节对系统性能的影响。为了避免高维数带来的设计复杂和难以实施问题，本文将控制器分为PI和PD两个独立部分并共用同一个规则库。选取误差e和误差的变化ec作为输入变量设计了二维的模糊控制器，将两个二维控制器的输出求和之后做为控制量u。这种简化后的模糊控制器本质上是一个非线性控制器，降低了总体复杂性，具有结构简单、易于应用、计算速度快等优点。

1 线径控制系统分析

护套生产线的工艺流程为：线芯经放线单元放卷后，在主辅牵引机构驱动下通过挤塑机机头；同时，颗粒状护套原材料经过除湿和加热处理后由旋转的螺杆推挤着从机头处挤出，在通过机头时根据生产规格选择合适的模具，从而使挤出的材料成形后可以紧密地包裹在线芯上形成电缆外护套；最后，经过冷却水定型完成喷码风干工序后由收线机构收卷成盘。挤塑机结构如图1所示。

图1 挤塑机结构

通过对挤塑机结构和护套挤出工艺流程的分析可知，覆盖外护套后的电缆线径主要取决于两个因素：护套原材料的挤出流率(实际生产过程中通过改变推挤速度即螺杆转速来控制)和主牵引速度。在主牵引速度恒定时，增加挤出流率则电缆线径增大；反之，线径减小。挤出流率恒定时，增大主牵引速度则电缆线径减小；反之，线径增加。在实际生产操作中，换卷后再次投入生产时为了达到设定生产速度，系统处于变速运行状态，牵引速度从0开始增加。为了保证线径稳定，需要通过增大挤塑机螺杆转速来增加塑料流率。当牵引速度达到设定的生产速度时，系统开始稳定运行[8]。由于改变推挤速度来控制线径的方式能从根源减少线经波动，因此在系统稳定运行时，本文采用调节推挤速度的方式控制线径。

线径控制系统结构见图2。图2中：挤塑机结构部分可等效为1阶惯性环节加纯滞后环节；调速系统是典型的闭环调速，可等效为2阶惯性环节。这样线径控制系统被控对象模型便可以用一个2阶惯性环节外加纯滞后环节来等效，传递函数形式为

G(s)=K1e-τs/(T1s+1)(T2s+1)

(1)

式中：K1是系统增益；T1、T2是由系统参数决定的时间常数；τ是滞后时间常数[9]。本文取被控对象的传递函数为

(2)

图2 线径控制系统结构框图

2 带Smith预估器的自适应模糊控制器设计

基于Smith预估器的自适应模糊控制器设计大致分为2个部分：自适应模糊控制器设计和用于滞后补偿的Smith预估器设计。

2.1 自适应模糊控制器设计

图3中，误差e和误差变化ec经过量化因子Ke、Kec变换到论域后作为模糊控制器的输入，经模糊推理后得到输出U；经过尺度变换、积分等运算输出uPD和uPI，相加后即得到总控制量u。这里的控制量u作用在推挤调速系统上，用来对推挤电机进行调速，进而控制电缆线径大小。取E、Ec、U的论域均为[-6，6]，模糊子集均为{NB、NM、NS、ZE、PS、PM、PB},隶属度函数曲线均取图4所示的曲线，控制器模糊规则如表1所示。

图3 自适应模糊PID结构

图4 模糊控制器隶属度函数曲线

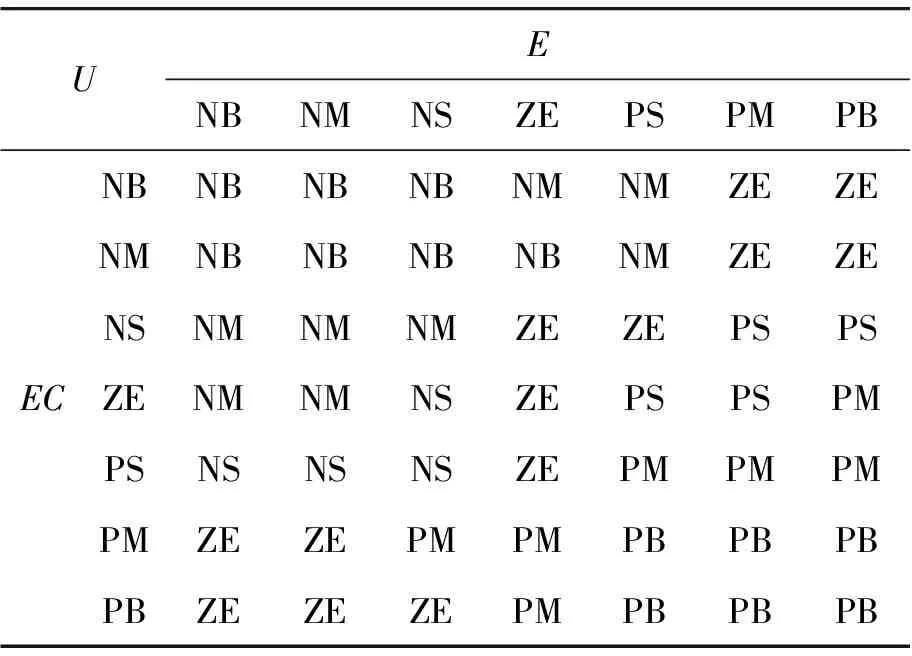
UENBNMNSZEPSPMPBECNBNBNBNBNMNMZEZENMNBNBNBNBNMZEZENSNMNMNMZEZEPSPSZENMNMNSZEPSPSPMPSNSNSNSZEPMPMPMPMZEZEPMPMPBPBPBPBZEZEZEPMPBPBPB

为使控制器具有一定自适应性，需要对控制器进行实时调整。调整模糊控制器的方法有很多种，控制规则的调整对系统性能影响较大，且不易实现；隶属度函数调整影响相对较小，但需要丰富的专家经验。因此，本文采用便于实现、效果明显[13]的可调参数调整。所设计的控制系统结构有Ke、Kec、α、β共4个可调参数。传统模糊控制器中参数Ke是由误差的取值范围和其论域范围的比例关系决定的，Kec同理。这里将二者设计为可调参数，用来调整误差及其变化的语言值，Ke、Kec增大，误差及其变化的语言值也增大，控制作用增强；反之减弱，相当于间接调整了模糊规则。权系数α、β用来调节比例、微分和积分作用。这个简化的模糊PID控制器可看做是在常规PD控制的基础上并联1个积分环节。通过调整α、β两个参数，控制器可实现PD、PI和混合PID功能。本文中虽设计了4个可调参数，但并不需要全部都做调整。由模糊推理后控制器的输入输出关系可知，β和Ke决定积分系数，α和Kec决定微分系数，比例系数由4个可调参数共同决定[14]，因此本文各选其一，通过调整β和Kec来研究系统的自适应能力。通过结合2阶纯滞后系统的阶跃响应曲线分析积分和微分环节的作用，得到误差和误差变化不同时β和Kec的调整规律，进而得到自适应调整模糊规则，见表2。

表2 自适应调整模糊规则

结合本文所取的具体系统传递函数，本文在仿真时取Ke=2.5，α=1.6，实时调整参数的初始值设为Kec=0.1，β=0.6,论域均取[-6,6]。

2.2 Smith预估器的设计

Smith预估控制是一种解决时间滞后系统控制问题的方法，其原理是：在传统负反馈结构的基础上引入补偿环节，将被延迟的误差信息提前反馈给控制器，消除滞后环节对系统的影响，提高了系统的响应速度和稳定性[15]。Smith预估器原理如图5所示(实际预估模型往往并不是并联在被控过程上，而是反向并联在控制器上)。

在模型完全匹配的情况下，即Gm(s)=Gp(s)τm=τ时，系统的闭环传递函数为

(3)

由式(3)可知：引入Smith预估器进行补偿之后，系统闭环传递函数的特征方程为1+Gc(s)·Gm(s)=0。可见，特征方程中不再含有滞后项，e-τs被移到了闭环控制回路之外，不再影响系统的稳定性[16]。

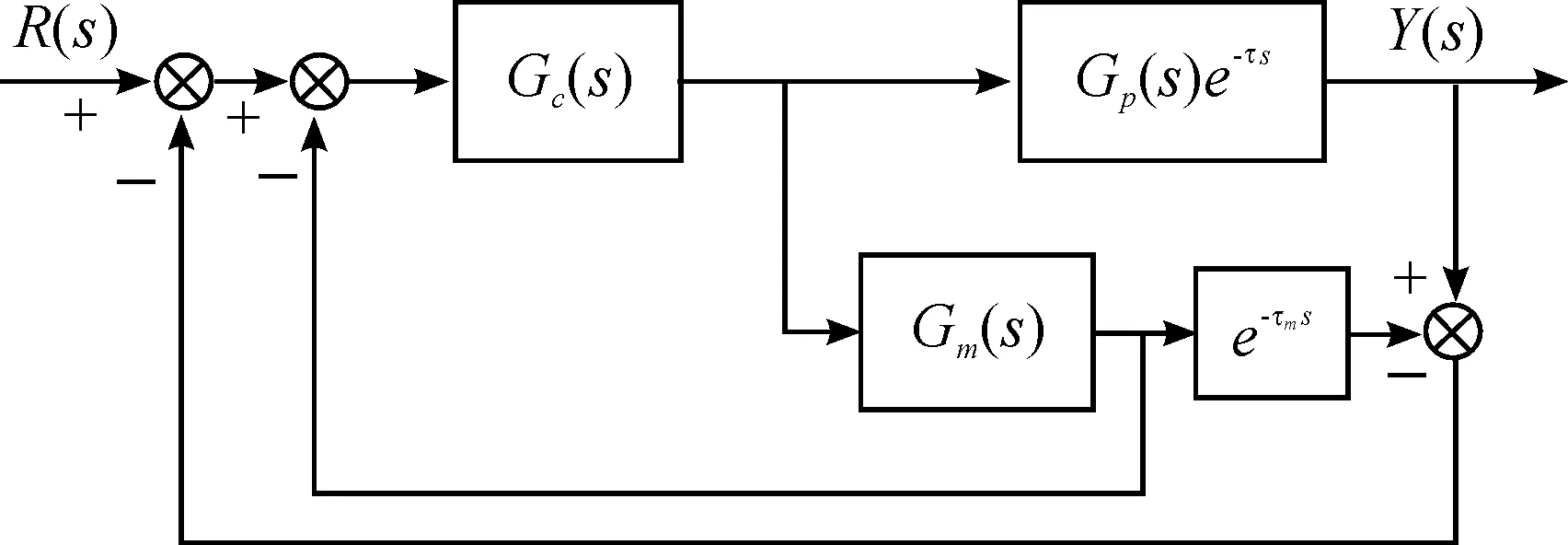
图5 Smith预估器原理

Smith预估器对被控对象模型的精确性有很高的要求，鲁棒性较差，在模型失配时会引起系统不稳定等问题。考虑到这些因素，本文采用一种具有参数自适应能力的Smith预估补偿方法。具体思路是在反馈通道增加1个辅助调节器，改进的Smith预估器结构如图6所示。

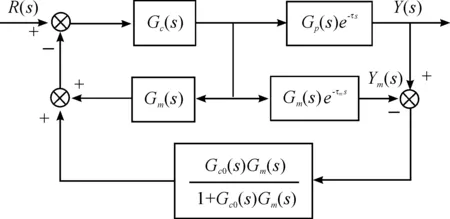
图6 改进的Smith预估器结构

According to the dynamics model of the manipulator,the healthy joints can be moved according to the desired position by PD control,and a global stability control in joint space can be realized.

(4)

其中：Tm为预估器时间常数；Kc为Gc0(s)增益Km是Smith预估器增益。

由此可见，增加辅助调节器后反馈通道传递函数由单位1变为1阶惯性环节。系统传递函数形式变为

(5)

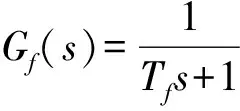
图7 带滞后补偿的控制系统结构

通过仿真分析发现：不同系统参数变化对Tf的要求是不同的。若模型失配仅由增益不同引起，即此时系统输出Y和预估器输出Ym的比值Y/Ym是一个常数，则不应引入滤波环节，此时应令Tf=0。若被控对象时间常数T变大，则应减小Tf，反之增大。对于滞后时间常数τ，不论怎样变化Tf都应存在，Δτ/τ的绝对值增大则Tf增大，反之Tf减小[18]。然而，被控对象的参数变化最终都会体现在系统输出和预估器输出的偏差eY及其变化ΔeY上，从偏差及其变化可以看出系统的当前工作状态。因此，整定参数Tf时往往先将初值设定在Tm左右，然后根据eY和ΔeY的变化情况实时调整Tf。这里eY和ΔeY的论域均取[-6，6]，模糊子集为{N、Z、P}，ΔTf的论域均取[-6，6]，模糊子集为{NB、NM、NS、ZE、PS、PM、PB}，隶属度函数均取高斯函数,改进的Smith预估器模糊规则如表3所示。

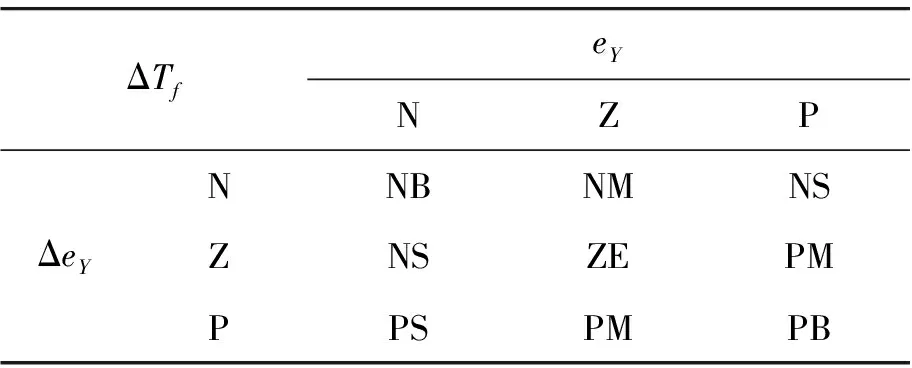
表3 改进的Smith预估器模糊规则

根据eY和ΔeY的大小，经模糊推理得到ΔTf。这样就可以实时调整Tf大小，得到一个参数自适应的Smith预估器。

3 系统仿真及结果分析

3.1 阶跃响应和抗干扰分析

根据所设计的控制系统在Simulink中进行仿真，其中改进的Smith预估器中参数Tf的自适应调整采用Matlab Function来实现。为比较不同控制方法的抗干扰能力，在25 s处加入大小为-1的扰动，系统参数不变时的扰动和阶跃响应曲线如图8所示。

图8 系统参数不变时的扰动和阶跃响应曲线

从图8可知：未加扰动时，采用传统PID控制，系统的超调量σ%约为18%，调节时间ts约为20 s，线径波动较大，系统跟随目标线径速度较慢；采用基于常规Smith预估器的AFPID控制，系统无超调，调节时间ts约为15 s，系统响应速度较快；采用基于改进Smith预估器的AFPID控制，超调量较小，调节时间约为18 s，线径变化较PID控制更为缓和。在抗干扰能力方面，由25 s后的响应曲线可以看出：基于常规Smith预估器的AFPID抑制扰动能力最强，几乎可以完全克服小范围扰动的影响，说明Smith预估控制在模型精确匹配时可有效克服滞后环节的不良影响，使控制效果得到明显改善。

3.2 参数鲁棒性分析

将系统纯滞后时间常数增大50%、增益变大20%，观察系统的阶跃和扰动响应曲线变化情况，比较不同方法对滞后时间变化的鲁棒性。系统参数变化时的扰动和阶跃响应曲线见图9。

图9 系统参数变化时的扰动和阶跃响应曲线

由图9可知：当系统滞后时间增大50%，增益变大20%后，传统PID控制的超调量有所增加，调节时间基本不变，整个过渡过程相对比较缓和，且系统仍然是稳定的，说明传统PID控制具有较强的鲁棒性。原本控制效果最好的基于常规Smith预估器的AFPID在系统滞后时间变化后超调量明显增加，系统各项性能也明显下降。基于改进Smith预估器的AFPID受滞后时间变化影响最小，仍能保证良好的控制效果。

仿真结果表明：基于常规Smith预估器的AFPID控制的阶跃响应各项性能指标和扰动抑制能力均优于传统PID控制，但在系统参数变化时的鲁棒性较差，采用改进Smith预估器后，这一问题得到解决。

4 结束语

本文通过对护套挤出工艺流程和挤出机结构的分析，得出了线径控制系统的数学模型结构和线径大小的影响因素。针对实际线径控制系统的特点和传统PID的局限性，提出了模糊控制和传统PID控制相结合的模糊PID控制方法，并在常规模糊PID控制器结构基础上进行变形、降维，得到简化和易于实际应用的模糊PID控制器。同时，通过设置可调参数的方法让控制器具有了一定自适应能力。考虑到实际线径控制系统的滞后性，引入了Smith预估补偿环节，并进行改进以适应系统参数的变化。最后，在Matlab的Simulink中对几种不同控制方法的扰动和阶跃响应曲线进行比较分析。结果表明，基于改进Smith预估器的自适应模糊PID控制表现出良好的控制效果、抗干扰能力和参数鲁棒性。

[1] 李帅.基于现场总线的光缆护套生产线控制系统设计[D].武汉：武汉理工大学,2011.

[2] 于强强.电线电缆生产线线径控制系统研究[D].长春：长春工业大学,2017.

[3] 武斌,张伟,金国文，等.模糊控制理论在工业控制工程中的应用实践探索[J].电子测试,2017(13):119-120.

[4] 周克良,李德福,聂丛楠,等.基于可变论域模糊PID的汽车烘房温控系统[J].江西理工大学学报,2017,38(3):68-74.

[5] 王春艳.基于Smith预估模糊PID的主汽温控制系统[J].工业控制计算机,2012,25(6):27-29.

[6] 张连会.基于Smith预估器的模糊PID温度控制算法研究[D].哈尔滨：哈尔滨工业大学,2012.

[7] 曾庆良,顾强,仉毅,等.基于Smith模糊PID控制的温室监控系统设计[J].计算机测量与控制,2015,23(6):1964-1966.

[8] 张淑风.电线生产线网络闭环系统智能控制的研究[D].呼和浩特：内蒙古科技大学,2009.

[9] 崔桂梅,穆慧灵,陈飞.优化模糊PID控制器在线径控制系统中的应用[J].高电压技术,2007(6):180-183.

[10] 张小娟.一种新型Smith Fuzzy-PID控制器的设计[J].热加工工艺,2012,41(4):210-212.

[11] 蔡成波,崔玉国,蔡永根,等.压电微动平台的改进PID控制[J].压电与声光,2016,38(3):441-444.

[12] 颜新鹏,王炯.基于模糊PID控制的空气弹簧振动特性研究[J].重庆理工大学学报(自然科学),2017,31(9):63-67.

[13] 李全俊,黄权,李锦.Smith预估模糊自适应PID控制在时滞系统中的应用[J].兵工自动化,2011,30(12):49-52.

[14] 曹学海.炭化系统中的模糊自适应PID设计及Smith预估器的改进[D].哈尔滨：东北林业大学,2016.

[15] 东方.基于Smith预估器的大时滞系统控制方法研究与仿真[J].制造业自动化,2010,32(8):177-179.

[16] 安连祥,马华民,刘永刚,等.基于改进Smith预估器的二阶时滞系统[J].计算机仿真,2011,28(1):198-200，233.

[17] 崔颖.基于Smith预估器的模糊PID控制方法研究[D].大连：大连理工大学,2006.

[18] 徐星星,张春,何慧云,等.基于改进Smith预估补偿及自适应Fuzzy-PID控制的NCS研究[J].陕西理工学院学报(自然科学版),2015,31(5):20-25.