风车状态下翼下吊架强度与振动分析方法研究

鞠明明，漆文凯，张嘉东

(南京航空航天大学 能源与动力学院， 南京 210016)

翼下吊架是大型飞机发动机与机翼的连接部件，主要用于传递发动机的载荷。随着我国飞机事业的发展，对于吊架的研究越来越深入。Thomas R H[1]介绍了一种研究吊架气动载荷特点的数值仿真方法；OLIVEIRA G等[2]针对ERJ145飞机吊架，采用CFD数值仿真方法，分析了吊架温度场引起的结构应力并进行了相关试验验证；KO A等[3]采用多学科分析方法和CFD仿真方法，分析了在跨声速条件下悬臂梁飞机吊架受机翼、梁相互干扰引起的气动载荷特点；薛彩军等[4]设计了一套吊架部段静力试验系统，采用载荷偏移与力偶施加相结合的方法，测试了3种危险工况载荷；宋波涛等[5]利用ANSYS软件建立吊架等效模型，在3种工况下分析了吊架结构的减振特性。而对于涡扇发动机来说，除了正常工作状态的载荷外，还有风车状态这一特殊状态下的载荷。LIM S K等[6]建立了一种基于发动机转速和质量流量的双转子发动机风车状态性能预测方法；ZACHOS P K[7]采用无量纲系数来描述风车状态特性，提出了一种预测风车内流阻力的方法，并进行了试验验证；AIAA等[8-14]介绍了不同类型涡扇发动机风车状态下的各种载荷，包括阻力载荷和振动载荷。章仕彪[15]论述了吊架强度设计要求，并给出了不同载荷条件下的吊架可靠性评价方法；唐兆田等[16]根据适航要求并结合风车载荷情况的特点，得出了适用于风车载荷条件下飞机强度的评定方法。

本文中建立了翼下吊架有限元模型，明确各个正常工况载荷，并对风车状态载荷进行了深入研究。在各种载荷工况组合下，建立一种吊架结构强度和振动特性研究方法，为吊架的设计提供一定的理论指导。

1 翼下吊架有限元参数化模型

对于大型飞机来说，翼下吊架是连接发动机与机翼的连接部件，主要分为3种结构形式[17]：阻力支柱式、盒式梁式和超静定式。选取超静定结构形式，在UG中建立吊架的参数化实体模型，然后导入到Workbench中进行有限元网格的划分，得到有限元参数化模型，如图1所示。

图1 翼下吊架有限元参数化模型

选取Solid185单元，节点个数为561 591，单元个数为114 679，材料为钛合金Ti-6Al-4V，弹性模量为118 GPa，泊松比为0.31，屈服强度为896.4 MPa。其中A、C两点为上接头和下接头，通过连杆与机翼相连；B为2个中间接头，直接与机翼连接；D为2个侧向接头，通过连杆与机翼相连。G点为发动机后挂点，包括4个抗拉螺栓和1个剪切销；E为发动机前挂点的左右2个吊耳，F为冗余结构挂点。

2 风车状态载荷

发动机由正常状态进入风车状态时，可以分为2个阶段[15]：第1阶段为瞬态风车阶段(高能阶段)，此时发动机未停车，通常持续几秒至几十秒；第2阶段为持续风车阶段(风车阶段)，发动机已停车，叶片在气流作用下仍然转动。

2.1 瞬态风车载荷

瞬态风车载荷是指发动机由正常工作状态到风车状态的过渡阶段所产生的载荷，此时发动机未完全停止工作，主要包括瞬态冲击载荷和转子卡滞载荷。

瞬态冲击载荷是指涡扇发动机叶片由于各种原因发生破裂，破损的叶片碎片会由于其高度性能而飞出，产生一个瞬态冲击载荷，这个载荷通过发动机传递到吊架的安装节处。碎片的大小不同，脱落角度不同，产生的冲击载荷也会不同。在这里给出一个冲击载荷计算公式：

(1)

式中：F为冲击载荷；m为碎片质量；n(r/min)为转子转速；R为脱落处距离中心转轴的半径;t为脱落时间。

转子卡滞载荷是指涡轮叶片由于外界原因(缺少润滑、温度场不均匀、导向器变形、转子失衡)导致叶片转速下降而产生的与转子转速反向的力偶。卡滞载荷作用在叶片安装节处，载荷大小与转速和转动惯量相关，计算公式如下：

(2)

式中：M为卡滞载荷；JX为叶片转动惯量；ω1为初始转速；ω2为终止转速；t0为卡滞时间。

转子卡滞与时间历程有很大关系，时间越短产生的力矩就越大，特别当转子瞬间卡死时，会产生非常大的扭矩，甚至能把安装轴扭断。卡滞产生的扭矩会通过转子支撑体系传到机匣，再传到发动机的安装节上。

2.2 持续风车载荷

持续风车载荷产生在发动机已完全进入风车状态的情况下，此时发动机已完全停止工作，转速降低到了稳定的风车转速，载荷主要包括风车阻力载荷和风车不平衡振动载荷。

风车阻力载荷是风车状态下，由于空气对发动机的阻碍作用而产生的。对于涡扇发动机来说，飞行马赫数Ma越大，风车阻力越大。下面给出一个风车阻力计算公式：

(3)

其中：ΔDW为风车阻力；ΔCDW为风车阻力系数，一般为0.001～0.015[18]；ρ为空气密度；SW为发动机迎风面积。

飞行马赫数增大，速度冲压压比迅速增大，涡轮可以有更大的膨胀比产生涡轮功带动压气机，所以风车转速随飞行速度的增加而增加。对于大涵道比涡扇发动机来说，外涵道流动阻力相对于内涵道要小得多，所以在风车状态下，大量空气从外涵道流过，如设计涵道比在56的发动机，风车状态下涵道比可达80∶1。风扇叶片处于大的负攻角状态工作，负荷极轻。

风车振动载荷发生在稳态风车工况下，使转子轮盘破裂进入风车状态，由于质量偏心而产生偏心振动，与偏心质量和转速有关。激励频率在一定频率内[16](一般可能为0～150 Hz)连续变化，理论上存在无数个频率点，每个频率点对应一套完整的动载荷。直接将全部动载荷用于结构的强度计算是不现实的，因此采用载荷系数的方法编制载荷谱。图2是某型涡扇发动机空中停车导致的风车不平衡振动加速度谱，是由飞机飞行实测载荷统计数据得出的[9]。

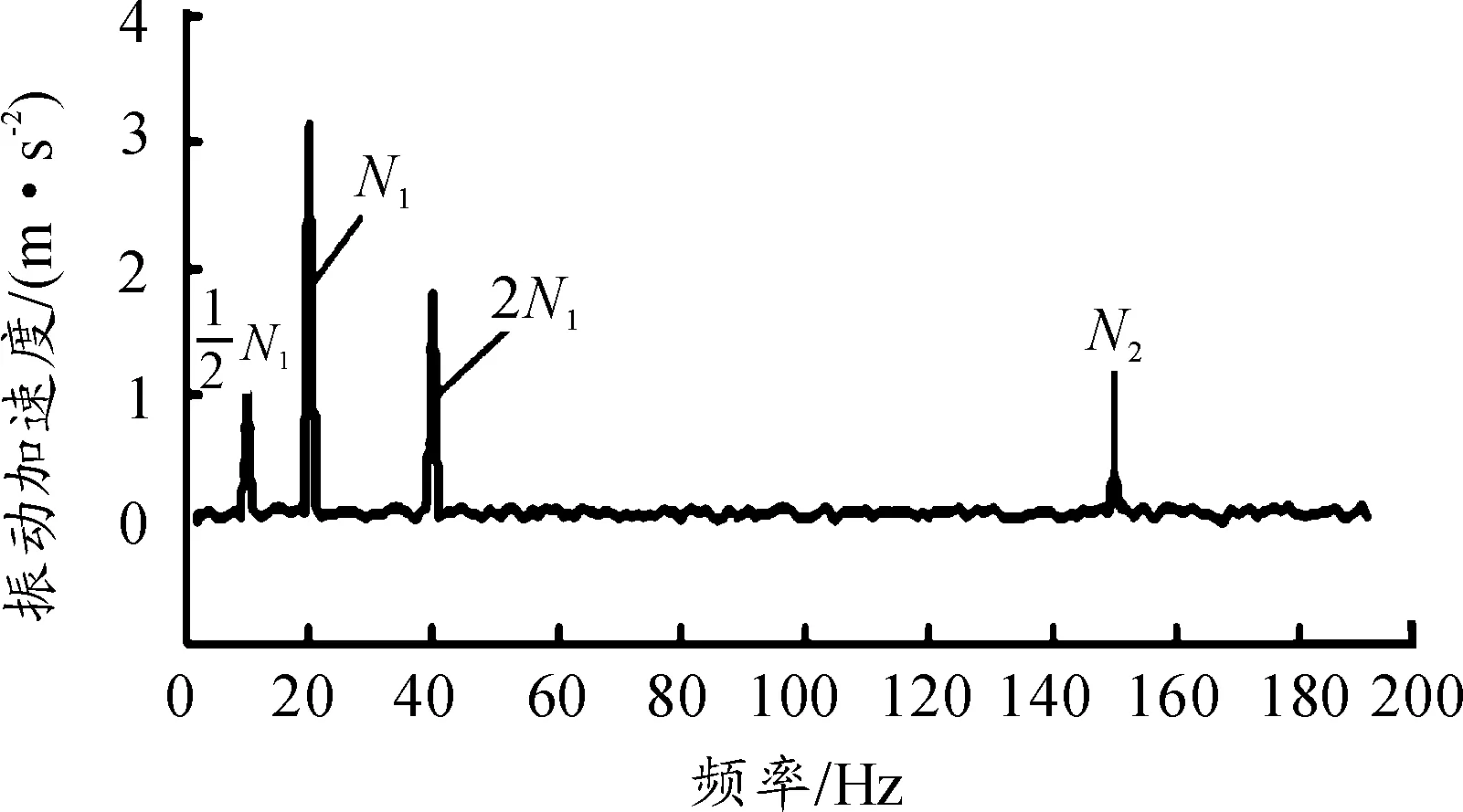
图2 风车不平衡振动加速度谱

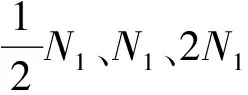
表1 风车载荷频谱

3 吊架强度与振动计算分析

3.1 边界条件

在Workbench软件中，对吊架的有限元模型的上接头A、中接头B、后接头C的位移约束为X、Y、Z三个方向上为0，绕X、Y方向角度约束为0，绕Z方向为自由约束；侧接头D的位移约束为X、Y、Z三个方向上为0，绕Y、Z方向角度约束为0，绕X方向为自由约束。

发动机本身惯性由E、G两处共同承担，推力由后挂点G处承担。因此，X方向载荷由发动机后挂点G来承担，Y和Z方向载荷由前、后挂点共同承担，前、后挂点承担的载荷比例根据具体发动机型号的重心位置和安装位置决定。

3.2 多工况静强度计算与分析

根据飞机飞行的各种工况，列出以下几种载荷工况[4,15]。其中1g表示发动机惯性1倍过载，本文中选取的发动机CFM56-3B-1型号，最大推力为92.50 kN，自质量为2 403 kg。根据CCAR-25-R4§25.303条，对于推力载荷取1.5安全系数，极限载荷可不取安全系数。

表2为吊架承受的正常工况载荷，工况1001和1002为发动机沿X方向的极限惯性载荷，工况1003和1004为转弯极限载荷，工况1005和1007为Z向极限载荷，工况1006和1008为最大推力状态下Z向最大极限载荷。其中，根据发动机的重心位置和安装位置，取前、后挂点承担的载荷比例为2∶1[20]。

在Workbench中计算以上8个正常工况组合，得到的应力和形变结果如表3所示。

表2 吊架正常工况载荷

表3 吊架正常工况计算结果

由表3可以得出：各工况中，最大应力为527.60 MPa，小于材料屈服强度827 MPa，因此吊架是安全的。而且在各个工况中，最大应力都发生在吊架侧向接头或后接头处，最大位移都发生在发动机前挂点。因此，应对应力集中处进行适当强化，例如添加加强筋或者增加材料厚度等；对于形变较大的前挂点，最大位移为8.305 5 mm，应适当提高结构的允许形变距离，保证结构的安全性。

3.3 风车工况计算与分析

根据风车工况的载荷特点，取3.1中的边界条件，并以单位力冲击载荷或单位扭矩载荷作为载荷工况边界，作用时间[15]取0.027 s,对吊架结构进行强度分析与计算。

根据吊架结构屈服极限为827 MPa，结合图3、4的计算结果，得出各个方向上所能承受的最大载荷。

图3 单位力冲击载荷应力变化

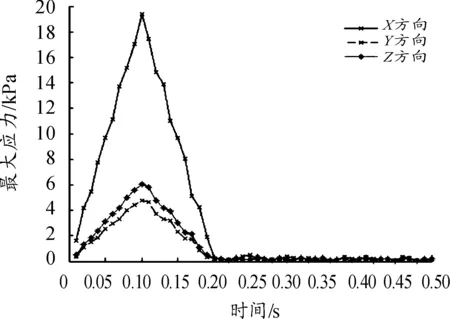
图4 单位扭矩载荷应力变化

边界条件单位力载荷/N单位扭矩载荷/(N·m)X2.05×1064.26×104Y2.67×1051.74×105Z7.07×1051.37×105

表4中，吊架各个方向上能承受的极限载荷是不同的，其中X方向能承受的极限载荷最大，表明在推力方向，吊架结构具有很好的强度特性，能很好地传递发动机的推理载荷。X方向上的扭矩极限载荷最小，这是因为吊架的发动机前挂点位置的宽度小于吊架结构的长度，且对于翼吊式飞机来说，惯性载荷大多是俯仰和转弯惯性载荷，因此该方向上的扭矩极限载荷满足本身吊架的结构强度。

根据图2的风车状态振动载荷谱，在Workbench中对吊架结构模型进行分析计算，得到的吊架位移响应结果如图5所示。

图5 风车振动载荷位移响应

从图5中可以看出：在风车外载荷谱的激励下，最大位移响应发生在吊架发动机前挂点附近。由于本文中的吊架模型是一个近似对称模型，所以吊架的位移响应相对于中截面是对称的，且越靠近发动机前挂点，位移响应值越大。

为了验证风车振动载荷形变的合理性，根据图2风车振动载荷的载荷谱，选取峰值振动频率，计算峰值频率下吊架的位移响应，结果如表5所示。

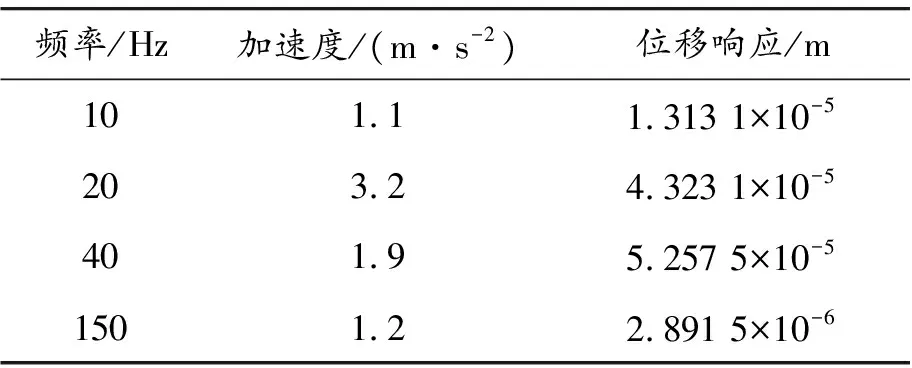
表5 峰值频率下吊架位移响应

由表5可以看出：在峰值频率下，吊架产生的最大形变在40 Hz处，且位置为吊架发动机前挂点附近，与图5中的最大位移响应位置相吻合。发动机频率与转子转速有关，吊架本身固有频率在Workbench中进行计算，得出前5阶为30.909、53.21、83.707、121.3、187.36 Hz。与图2中的峰值频率进行对比分析，结果表明：发动机峰值频率与吊架结构本身固有频率相差很大，不会产生共振。

4 结束语

1) 参考已有的翼下吊架结构形式，改进设计了一种后传扭的超静定式吊架结构有限元模型，能更好地传递发动机的载荷；

2) 对风车工况这种非正常工况进行了载荷研究，并根据载荷特点进行了分类，根据风车的时间历程，结合CCAR-25的相关规定，分为瞬态风车载荷和持续风车载荷；

3) 在正常工况和风车工况下，对吊架模型进行了强度和振动特性研究，建立了一种多工况条件下吊架载荷传递响应分析方法，并对该方法进行了验证；

4) 发动机载荷通过吊架传递到飞机机翼，最终传递到机身，本文方法可用于研究吊架载荷传递的强度和振动特性，同时对吊架本身的结构设计有重要的参考意义。

[1] THOMAS R H.Computational Analysis of a Pylon-Chevron Core Nozzle Interaction[M].Washington:NASA Langley Technical Report Server,2001:1-12.

[2] OLIVEIRA G,SANTOS L,TRAPP L.Conjugate Heat Transfer Methodology for Aircraft Pylon Analysis[C]//21st AIAA Applied Aerodynamics Conference,2003:1-11.

[3] KO A,MASON W,GROSSMAN B.Transonic Aerodynamics of a Wing/Pylon/Strut Juncture[J].AIAA Journal,2006.

[4] 薛彩军,谭伟,聂宏.民用飞机发动机吊挂静力试验技术研究[J].实验力学,2011,26(6):735-742.

[5] 宋波涛,贺尔铭,张钊.翼吊发动机吊架结构等效建模及减振特性分析[J].科学技术与工程,2012,64(4):832-835.

[6] LIM S K,ROH T S,HONG Y S,et al.Study of windmilling characteristics of twin-spool turbo-fan engines[C]//Aiaa Aerospace Sciences Meeting & Exhibit.Salt Lake City:AIAA,2002.

[7] ZACHOS P K.Modelling and Analysis of Turbofan Engines Under Windmilling Conditions[J].Journal of Propulsion & Power,2013,29(4):882-890.

[8] AIAA.Vibraisolation of Power Plants for New Generation Airplanes with Engines of High by-Pass Ratio[J].AIAA Journal,2003.

[9] 白杰,李广,王伟.大型客机风车不平衡振动载荷传递特性研究[J].机械工程与自动化,2015(4):11-13.

[10] 黄求原,汤彬,周淼.民用大涵道比分排涡扇发动机风车状态初步研究[J].民用飞机设计与研究,2013(s2).

[11] 张媛,马燕荣,郭斌.某型发动机风车特性试验研究[J].现代机械,2015(3):73-76.

[12] 王占学,刘增文.某型燃气涡轮发动机风车状态内阻力的计算[J].燃气涡轮试验与研究,2006,19(3):8-10.

[13] 王占学,王永杰,乔渭阳,等.涡扇发动机低转速部件特性扩展和风车状态性能模拟[J].推进技术,2006,27(2):146-149.

[14] 何时慧,吴国钏.涡扇发动机风车特性计算[J].航空发动机,1997(3):1-9.

[15] 章仕彪.民用运输机吊挂设计强度要求研究[J].民用飞机设计与研究,2012(1):27-31.

[16] 唐兆田,赵剑军.风车载荷情况下民用飞机结构强度评定方法[J].民用飞机设计与研究,2016(2):20-22.

[17] 刘亚奇,胡锦旋,刘星北,等.翼下发动机吊架及其与机翼连接结构研究[J].民用飞机设计与研究,2009(s1):74-76.

[18] 黄太平.飞机性能工程[M].北京：科学出版社,2005:20-21.

[19] 刘晓明,万少杰,熊俊江,等.民机飞行载荷谱编制方法[J].北京航空航天大学学报,2013,39(5):621-625.

[20] 陈光.航空发动机结构设计分析[M].2版.北京:北京航空航天大学出版社,2014.