正交曲面坐标系中非线性热本构方程
苗亚男,李 忱,冯启隆,王海任
(太原科技大学 太原 030024)
薄壳结构因其具有独特的几何结构和良好的受力特点,所以在航空航天、海洋输油管道、天然气运输和核电等领域有着广泛应用。承压容器大多属于薄壳结构,强度不足和屈曲失稳是承压容器失效破坏的主要形式,尤其失稳破坏时常没有任何征兆,会引起巨大的安全隐患和经济损失,所以薄壳结构稳定性问题一直受到人们的关注。
本文从各向同性材料非线性热本构方程出发,仅考虑温度初值和增值的情况,研究了各向同性材料非线性热本构方程。基于平面应力假设和直法线假设,推导出曲线坐标系下的热本构方程。而大多数薄壳结构都是在正交曲线坐标系下进行研究,所以将张量函数变换到正交曲线坐标系中非线性热应力本构方程具有重要的意义。
1 非线性热本构方程
弹性材料不仅在外力作用下因素下所产生的应力,温度变化也会使弹性体产生应力、应变和位移。在仅考虑温度初值和增值的情况下,根据文献[1,2]得到各向同性材料的非线性热本构多项式:

(1)
将热应力本构方程一次形式和二次形式相加并整理,最终得到非线性各向同性弹性材料热应力本构方程为:
(2)
2 几何方程
2.1 正交曲线坐标系下的几何方程
正交系中,协变基矢量gi互相正交,但不一定是单位基矢量。其长度为:
|gi|=Ai(i=1,2,3)
式中Ai(i=1,2,3)表示拉梅常数。
将协变基矢量gi变为一组正交标准化基ei(i=1,2,3)

通过christoffel符号表示基矢量对坐标的导数。在正交系中有:
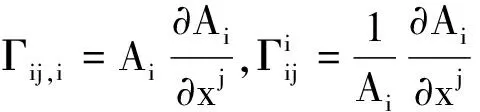
(3)
正交曲线坐标系中小应变张量的分量和位移矢量的物理分量的几何关系为[3]:


(4)
其中对正交标准化基ei对坐标求导由式(3)和式(4)可知:
(5)
(6)
上述两式可以写成:
(7)
将式(7)代入式(4),得到正交曲线坐标系中位移分量表达的几何关系,定义下标1-11,2-22,3-33其中为:
(8)
2.2 壳体的几何方程
壳体中面任意一点M沿x1,x2及x3方向(如图1所示)的拉梅系数为
A1=h1(1+k1x3),A2=h2(1+k2x3),A3=1


图1 受力示意图
Fig.1Sketchofforce
根据垂直于中面方向的线应变可以不计,得到ε3=0;
根据直线法假设,即:ε31=0和ε23=0
由式(8)中的第五,六式,应用x1,x2及x3方向的拉梅系数并以w代替u3对x3进行从0到x3积分,令中面任意一点M沿x1和x2方向的位移分别为u和v,求得:
求解得到u1,u2和u3分别为:
(9)
将式(9)代入式(8)得到壳体应变分量和中面位移的关系式
(10)
简写为:
(11)
式中
(12)
3 非线性热本构方程
非线性各向同性弹性材料热本构方程为:
(13)
用通用符号表示,得到
σij=(k1εmm+k3εmmεmm+k4εij+δ1Τ+δ2Τ2+δ3εmmΤ)δij+2(k2+k4εmm+δ4Τ)εij+3k5δijεijεij
(14)
得到正交曲线坐标系下的非线性热应力应变关系:
σ12=bε12+g(ε1ε12+ε2ε12)+hε3ε12+kε23ε13+2δ4ε12T
σ23=bε23+g(ε2ε23+ε23ε3)+hε1ε23+kε12ε13+2δ4ε23T
σ13=bε13+g(ε1ε13+ε3ε13)+hε2ε13+kε12ε23+2δ12ε13T
(15)
在正交曲线坐标系下对三维弹性体的应力应变关系根据平行于壳体中面的各层互不挤压,即:σ3=0,和直法线假设:变形前垂直于中面的直线在变形后仍保持直线,并仍垂直于变形后的中面。即:σ13=σ23=0.得到壳体的热应力表达式为[4]:
σ12=bε12+g(ε1ε12+ε2ε12)+2δ4ε12T
(16)
对于薄壳来说,对中面内力N1,N2,N12和内力矩M1,M2,M12近似表示为[5,6]
(17)
将式(11)、式(16)代入式(17),得到壳体非线性热内力和非线性热内力矩分量:
(18)
4 结论
本文从张量函数出发,基于应变和温度为变量的双变量非线性热本构理论,对各向同性材料弹性薄壳的非线性本构方程和非线性热本构方程进行了分析,得到以下几个结论:
1)在曲线坐标系下。各项同性材料n=2时弹性张量的个数是5个,与文献[1]的结论吻合。
2)可以将弹性薄壳的非线性本构方程和非线性热本构方程退化得到线性本构方程和线性热本构方程,得到的结果与文献[4,7]中的方程是的一致。
3)本文从张量函数角度出发,推导出正交曲线坐标系下的非线性本构方程和非线性热本构方程。由此可以进一步得到球壳,圆柱壳等形状的非线性热应力应变关系。
4)由于现实中需要解决的问题大都是非线性的所以薄壳的非线性本构方程具有很重要的现实意义。
参考文献:
[1] 李忱.超弹性体非线性本构理论[M]. 北京:国防工业出版社,2010.
[2] 赵丽,李忱.非线性各向同性弹性材料热应力本构方程[J].应用数学与力学,2013,34(2):183-189.
[3] 黄克智,薛明德,陆明万.张量分析[M].北京:清华大学出版社,2009.
[4] 田雪坤,李忱,王海任,等.球坐标非线性热应力本构方程[J].太原科技大学学报,2014,35(6):464-468.
[5] 韩强,黄小清,宁建国. 高等板壳理论[M]. 北京:科学出版社, 2002.
[6] 曹富新.力学中的张量计算[M]. 北京:中国铁道出版社,1985.
[7] 徐芝纶. 弹性力学简明教程[M].3版. 北京:高等教育出版社, 2002.

