连续控制系统固定步长离散化方法性能对比分析

赵广辉，高 鑫，方金福，张青青，于伟民，姚 冰

(1.辽宁科技大学 机械工程与自动化学院,辽宁 鞍山 114051；2.营口理工学院，辽宁 营口 115000 3.沈阳飞机设计研究所 飞行控制部,辽宁 沈阳 110035)

在现代工业生产中，控制系统扮演着越来越重要的角色.由于信息技术的快速发展，控制系统中引进离散控制方式执行控制算法的做法越来越普及[1].由于连续控制系统设计有着完善的理论基础，因而利用连续控制器理论设计离散控制器，使离散控制器能模仿连续控制器的特性是一种比较方便和流行的做法，这个过程也被称作连续系统的离散化.离散化从不同控制系统角度来说，分为固定步长(Fixed Step)和可变步长(Variable Step)两种模式.常见的控制系统具有稳定的控制计算周期，因而较多采用固定步长模式，这也是本文所研究的系统控制模式.

为研究方便，一般的控制系统可以表示为输出量的微分方程，其中微分方程的阶数也是控制系统的阶数.为不失一般性，同时兼顾推导过程的简洁，本文以一阶系统为例，研究不同离散化方法计算一阶系统时域响应的时间性能和离散化误差，并进行横向对比，从而选择出最优方法.一阶系统的等效微分方程为：

(1)

假设系统的s域传递函数为G(s)，这里为分析方便只需研究开环响应，那么系统的等效框图如图1所示.

图1 开环系统等效框图

1 固定步长离散化方法

1.1 欧拉法(Euler法/前向差分法)

根据z变换理论[2]，对于控制系统，从连续域(s域)到离散域(z域)的映射公式为

z=esT，

(2)

其中，T为采样周期.

上式可作如下变换：

z=esT≈1+sT，

(3)

即

(4)

式(4)两边同时乘以输出信号Y，并分别作各自频域逆变换得到

(5)

那么

yk+1=yk+Ty′=yk+Tf(xk,yk).

(6)

式(6)即为欧拉(Euler)法近似公式，欧拉法也称前向差分法.

以积分器为例，其传递函数为[3]

(7)

时域表达式为

y′=f(x,y)=x.

(8)

使用式(6)得到的积分器欧拉法离散化计算公式为

yk+1=yk+Txk.

(9)

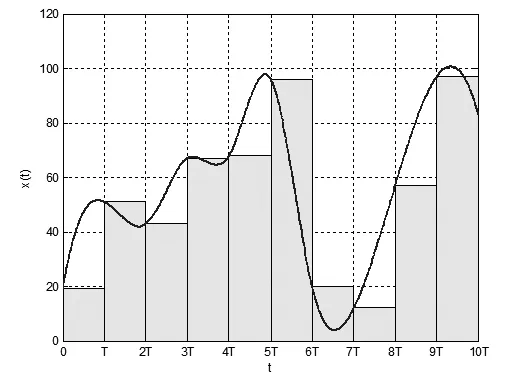
图2 使用欧拉法离散化积分器的面积近似图

图2为使用欧拉法离散化积分器的面积近似图.其中，曲线表示连续系统中真实的x(t)，其与横轴所围面积代表积分器的实际输出.柱状图代表x(t)在每个离散化时间点的采样值，所有矩形的面积之和即为使用欧拉法近似的积分器离散化输出面积.可以看出，欧拉法在每个离散化时间点都会产生误差，并且随着时间的推移误差会逐渐累积.一般来说，欧拉法的全局离散误差[4]为0(T)，即误差大小和离散化时间间隔线性相关，这在工程上是不可接受的.

1.2 双线性变换法(Tustin法)

式(2)也可作如下变换

(10)

即

(11)

那么对于传递函数为G(s)的连续系统，其在z域的表达式为

(12)

式(12)即为双线性变换法在频域上从连续域到离散域的变换公式.双线性变换法也称Tustin法[5].

仍以积分器为例，将式(7)代入式(12)中，可得

(13)

对式(13)应用z逆变换，时域表达式为

(14)

图3为使用双线性变换法离散化积分器的面积近似图.折线图代表x(t)在每个离散化时间点的采样值，所有梯形的面积之和即为使用双线性变换法近似的积分器离散化输出面积.可以看出，和欧拉法的矩形近似相比，双线性变换法的梯形近似离散化误差更小，精度更高了.

1.3 休恩法(Heun法)

式(11)也可作如下变换

(15)

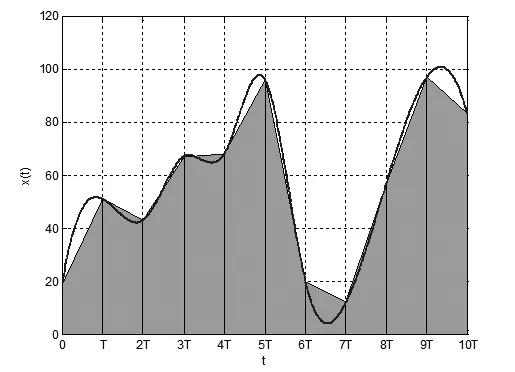
图3 使用双线性变换法离散化积分器的面积近似图

式(15)两边同时乘以输出信号Y，并分别作各自频域逆变换得到

(16)

那么

(17)

式(17)中等号右边的f(xk+1,yk+1)中yk+1为未知数，要继续求解，需要一个估计值，欧拉法的解能够满足这一目的，将其代入式(17)中后，得到休恩(Heun)法的解：

(18)

对于式(7)中的积分器，使用休恩法进行离散化的过程和双线性变换法相同，因而离散化积分器的面积近似图也和图3一致.这是因为积分器的时域表达式(即式(8))仅与x有关，那么式(18)中关于pk+1的计算就可以忽略，故而使用休恩法对积分器进行离散化得到的时域表达式与双线性变换法相同.但是对于其它动态环节(尤其是时域表达式与y有关的)，由于休恩法的第一步进行了欧拉法近似估值，会导致其离散化误差通常情况下比双线性变换法要大一些，离散化精度相应低一些，这一点在后面的仿真分析里会提及.

1.4 泰勒级数法

1.4.1 泰勒定理 设y(t)∈CN+1[t0,b]，且y(t)在不动点t=tk∈[t0,b]处有N次泰勒级数展开[6]：

y(tk+T)=y(tk)+TAN(x(tk),y(tk))+O(TN+1)，

(19)

其中，

(20)

式(20)中的y(j)(t)=f(j-1)(x,y)表示函数f关于t的(j-1)次全导数.

N次泰勒方法的一般步骤为

(21)

其中，在每步k=0,1,…,M-1有

dj=y(j)(tk),j=1,2,…,N.

1.4.2 龙格-库塔(Runge-Kutta)法 泰勒方法的优点是最终全局误差的阶为0(TN)，并且可以通过选择较大的N来得到较小的误差.然而泰勒方法的缺点是，需要先确定N，并且要计算高阶导数，它们可能十分复杂.每个龙格-库塔(Runge-Kutta)方法都由一个合适的泰勒方法推导而来，使得其最终全局误差为0(TN).一种折中方法是每步进行若干次函数求值，从而省去高阶导数计算.这种方法可构造任意N阶精度的近似公式，最常用的是N=4阶龙格-库塔方法(RK4).

标准的N=4阶龙格-库塔方法计算过程如下：

(22)

RK4适用于一般的应用，因为它非常精确、稳定，且易于编程.许多专家声称，没有必要使用更高阶的方法，因为提高的精度与增加的计算量相抵消.如果需要更高的精度，则应该使用更小的步长或某种自适应方法.

1.4.3 Bogacki-Shampine法 更小的N阶泰勒方法具有较低的精度，使计算过程更加简便，也更易于理解.N=2的2阶龙格-库塔方法(RK2)中的一种情形会退化为休恩法，计算过程如式(18)所示.

N=3的3阶龙格-库塔方法中最有名的是Bogacki-Shampine法(BS3)，其发明者Bogacki和Shampine声称这种方法是所有3阶龙格-库塔方法中性能最好的.

Bogacki-Shampine法计算过程如下：

(23)

2 性能对比分析

2.1 时间性能分析

为分析各离散化方法的计算效率，以常见的一阶系统作为分析对象，考察各个方法在对一阶系统进行离散化时的时间性能，这里以一次迭代需要进行的浮点数加法和乘法计算次数来衡量[7].

典型的一阶系统的传递函数为[8]

(24)

时域表达式为

(25)

将式(25)代入式(8)、(18)、(22)和(23)分别可得应用Euler法、Heun法、BS3法和RK4法离散化一阶系统的计算过程.而将式(24)代入式(12)再做z逆变换可得应用双线性变换法离散化一阶系统的计算过程.所有方法的时间性能对比如表1所示.

表1 不同离散化方法时间性能对比

根据表1中的时间性能可知，不同离散化方法的计算效率差别很大.考虑到进行一次浮点数乘法的时间远大于进行一次浮点数加法的时间，那么根据表1可得出下列结论：

(1)RK4法计算过程最复杂，耗时最多，但基本和BS3法不相上下；

(2)Heun法比Tustin法耗时稍多一点，二者所需时间差不多是RK4法和BS3法的1/5左右；

(3)Euler法耗时最少，所需时间是Heun法和Tustin法的一半左右.

2.2 离散化误差分析

仍以一阶系统为分析对象，下面比较各离散化方法的离散化误差.式(24)所表示的一阶系统的单位阶跃响应时域表达式为

h(t)=1-e-t/τ,t≥0.

(26)

其中输入为单位阶跃函数[9]

(27)

以式(27)所表示的单位阶跃函数为输入，分别使用5种离散化方法对式(24)所表示的一阶系统进行离散化计算，得到离散化的输出，并与式(26)的预期结果进行作差，即可得到不同离散化方法的离散化误差.

这里假设采样间隔T=0.01 s[11]，仿真时间为10 s，一阶系统参数τ=2，式(26)的输入经过离散采样后xk=u(t)|t=tk=1，初值y0=0.离散化误差表达式为

err(tk)=|yk-h(tk)|.

(28)

图4和图5所示为不同离散化方法一阶系统单位阶跃响应时域输出以及离散化误差对比示意图.5种方法全局离散化误差为各自误差曲线与时间轴所围面积，在仿真中的结果分别为0.48、8e-4、4e-4、1e-6和1e-9，从以上仿真可以得出如下结论：

(1)Euler法、Heun法、Tustin法、BS3法和RK4[12]法离散化误差分别递减，单点最大误差均出现在仿真时刻第τ=2s处，数量级分别为10-3、10-6、10-7、10-9和10-12；

(2)Euler法的全局离散化误差为0(T)，这在工程应用中一般是较大的，因此实际控制系统已经很少采用Euler法作为离散化方法；

(3)Heun法和Tustin法的全局离散化误差均为0(T2)，只是前者的常系数较大而已.从仿真结果可以看出，Tustin法的离散化误差大约是Heun法的一半左右，这与1.4.3中对两种离散化方法的对比分析结论一致；

(4)BS3法[13]和RK4法的全局离散化误差分别为0(T3)和为0(T4)，与理论分析一致；

(5)从单点离散化误差来看，Tustin法和RK4法分别为10-7和10-12数量级.值得一提的是，在实际控制系统中采用何种离散化方法还与所选用的浮点数精度有关.如果离散化所选用的为32位浮点数，根据IEEE754[14]，其十进制有效数字仅为7～8位，此时选择Tustin法完全能够满足要求，选取精度更高的离散化方法已经没有必要；如果所选用的为64位浮点数，则其十进制有效数字为15～16位，选择RK4法虽不能完全覆盖其最高精度，但在实际工程中10-12数量级的误差基本可以等价于0，故而是可行的选择方案.

3 结束语

本文介绍了连续控制系统中常用的5种固定步长离散化方法，从时域和频域两方面对每种方法的计算过程做出推导，并对各种方法的异同给出了简单介绍.以一阶系统为分析对象，从时间性能和离散化误差两方面对5种方法的性能做出对比分析.仿真分析结果表明：

(1)Euler法虽然时间性能良好，但由于离散化误差较大而不能适应控制系统的精度要求；

(2)Heun法无论在计算效率还是离散化误差性能均不如Tustin法，因而可以完全被Tustin法代替；

(3)BS3法计算效率和RK4法基本相同，但全局离散化误差却高了很多，因而也应该被RK4法所代替；

(4)从时间性能和离散化误差两方面来说，在实际工程应用中最广泛使用的就是Tustin法和RK4法两种离散化方法.两种方法的综合性能明显优于其它方法，但受浮点数精度制约，应用场合应有所不同.当所使用的浮点数为二进制32位时，采用Tustin法既能获得很好的计算效率，又可完全满足精度要求；而当所使用的浮点数为二进制64位时，采用RK4法可获得最佳的综合性能.

图4 不同离散化方法一阶系统单位阶跃响应

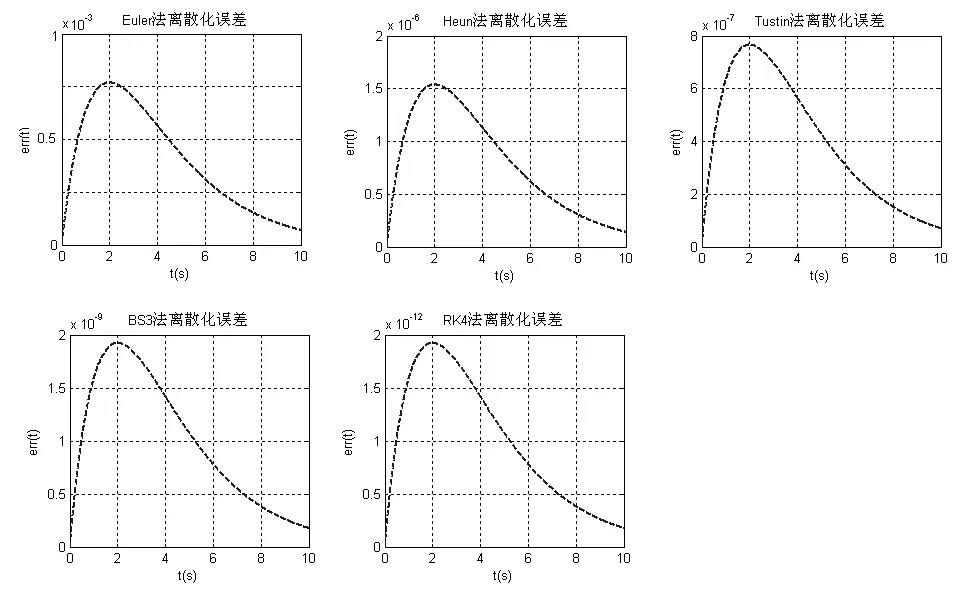
图5 不同离散化方法离散化误差对比

[1] 赵霞，王祝萍，贾海航.连续系统离散化方法的比较与解析初探[J].工业和信息化教育,2015,10:71.

[2] 胡寿松.自动控制原理[M].北京:科学出版社,2011：319-320.

[3] Alan V，Oppenheim Alan S，Willsky with S,et al.Signals & Systems[M].(Second Edition)西安:西安交通大学出版社,1999：497.

[4] John H Mathews，Kurtis D Fink.数值方法(MATLAB版)[M].周璐，陈谕，钱方，等译.北京:电子工业出版社,2010.

[5] 刘瑞叶，任洪林，李志民.计算机仿真技术基础[M].北京:电子工业出版社,2011：62.

[6] 同济大学数学系.高等数学[M].北京:高等教育出版社,2007：139-141.

[7] Randal E Bryant，David R O’Hallaron.深入理解计算机系统[M].北京:机械工业出版社,2011：534-536.

[8] Katsuhiko Ogata.现代控制工程(英文版)[M].北京:电子工业出版社,2014：122.

[9] 王正林，王胜开，陈国顺，等.MATLAB/Simulink与控制系统仿真[M].北京:电子工业出版社,2011：110.

[10] IEEE 754:Standard for Binary Floating-Point Arithmetic[C/OL].http://grouper.ieee.org/groups/754/,2012:118-121.

[11] 王向阳，金海波.低比特率Bandelet域图像压缩编码算法研究[J].辽宁师范大学学报(自然科学版),2012，35(3)：321-323.

[12]白乙拉，李冰，冯景山.以气温为边界条件的水库冰盖厚度的数值模拟研究[J].辽宁师范大学学报(自然科学版),2012，35(2)：164-166.

[13] 杨忠志,徐珍珍.应用Fukui函数探讨双苯基-取代的自由基闭环反应的区位选择性[J].辽宁师范大学学报(自然科学版),2012，35(2)：193-195.

[14] 刘小丹，孙晓奇，沈滨.基于EMD的信号瞬时频率估计[J].辽宁师范大学学报(自然科学版),2009，32(1)：58-60.