月球着陆器用磁流变液缓冲器设计与研究
赵鑫光,陈金宝,王宸,魏君
(南京航空航天大学 航天学院,江苏 南京 210016)
0 引言
磁流变液(MRF)是一种通过在特定的载液(硅油、矿物油等)中添加磁性粒子形成的“智能”悬浮液。无磁场时,磁流变液呈现出流体的状态;施加磁场时,呈现出半固体的状态。目前,它已经在工业中得到广泛应用,包括缓冲器、阻尼器刹车和离合器等[1-3]。
目前,很多国家都对磁流变液进行了研究,其中美国在磁流变液工程化应用方面做出了突出的贡献。1991年,TRW公司的Shtarkman研制了一种应用到汽车悬架主动控制系统中的旋转式吸震器;1993后, Lord公司在磁流变液研制方面取得很多重要成果,并已有多款产品面市[4];Notre Dame 大学的Dyke和Spender等人将其应用到了大型结构的地震响应控制中; Ford公司的 Ginder等人通过有限元分析软件分析了磁流变液的屈服应力[5];GM公司的Foister和Gopal Swamy等人研制了几种磁流变液和磁流变离合器[6-8];美国加州州立大学的Zhu和Liu 等人对磁流变液微观结构的流变特性进行了研究;美国匹兹堡大学的Gence和Phule 对不同尺寸粒子的磁流变液的屈服应力进行了研究[9];Ciocanel等人根据粒子对模型建立了磁流变液的动力学理论,并推导了在不同磁感应强度和剪切速率下的磁流变液的瞬态剪切应力[10]。
除此之外,德国BASFAG 的Kormann 等人研制了稳定的纳米级磁流变液;日本的Yamagata 大学对磁流变离合器进行了研究[11];白俄的Kordonski等人在磁流变液性能以及磁流变抛光、密封等方面的研究取得了重大进展;法国Nice 大学的Bossis 和Cutillas等人对磁流变液的流变机理以及微观结构进行了大量的研究;韩国Inha 大学对车载可控保险杠磁流变缓冲器进行了研究[12]。
在国内主要是研究所和高校对磁流变液的流变机理、产品开发、控制策略和应用进行了一些研究,并取得了一定的成果。重庆材料研究所研制了一种桥梁拉索抗风振阻尼器,并应用到重庆外环观音岩大桥上;哈尔滨工业大学的欧进萍、关新春等人研制了不同尺寸和类型的磁流变液阻尼器,并应用到山东滨州黄河大桥和渤海某海洋平台的振动控制中[13-15]。
通过工业应用,人们在磁流变液的设计和生产制造方面已经积累了大量的经验,并且其应用到月球着陆器的可行性由李洪波得到验证[16]。月球着陆器在最终着陆阶段会受到强烈的冲击,缓冲系统在此过程中将发挥重要作用。目前,“软着陆”是着陆的主要形式,表1是目前被广泛使用或研究的3种缓冲器,液压缓冲器、铝蜂窝缓冲器和磁流变液缓冲器的性能比较。
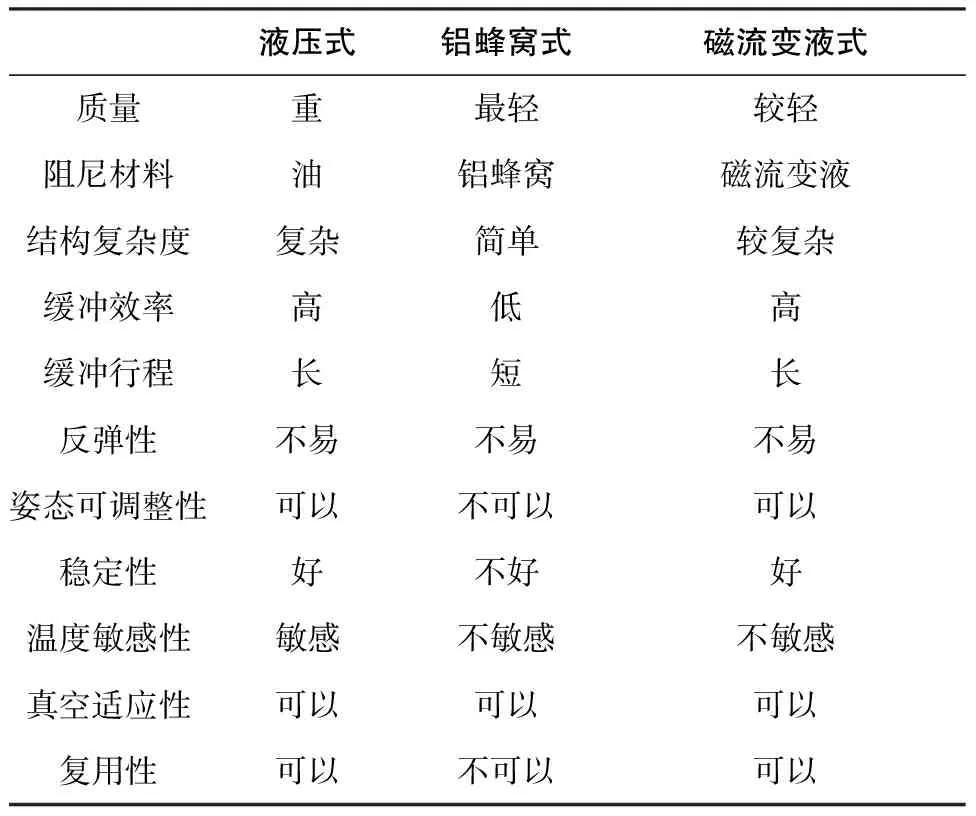
表1 3种缓冲器的性能比较
由表1看出,和铝蜂窝缓冲器相比,磁流变液缓冲器具有高缓冲效率、长缓冲行程、姿态可调整、良好的稳定性和可重复使用的优势。并且,和液压缓冲器相比,它还具有质量较轻和温度不敏感的优点,这在缓冲器的设计中尤为重要。
通常,软着陆的时间在0.5s左右,因此对磁流变液缓冲器的控制策略要求很高。由于在线计算时间短,像状态控制的半主动控制策略被广泛研究并应用到磁流变液缓冲器的控制中。时间延迟可以被急剧减小,使得将其应用到月球着陆器的缓冲系统中变成可能。同时,随着我国地外天体探测的深入发展,需要研制出一种可以在复杂着陆环境中使用的着陆缓冲系统。因此,磁流变液缓冲器是设计中一个不错的选择。
1 缓冲器选择
MRFD通常被分成以下4类:
1) 单头阀式
2) 单头剪切阀式
3) 双头剪切阀式
4) 双头旁路剪切阀式
月球着陆器通常会被从一个设定的高度以一定的初始速度释放,且不能承受大过载,则需要缓冲器具有较大的缓冲行程。和单头式相比,双头式一般具有更大的缓冲行程,其中旁通式的设计,使其更易于进行热控制,则双头旁路剪切阀式缓冲器在应用到月球着陆器中,具有独特的优势。
因此,选用双头旁路剪切阀式缓冲器作为研究目标,结构简图如图1。L0、L为主缸和旁通缸的长度;D0、D为主缸和旁通缸的直径;vh为活塞的速度;Lh为活塞的厚度;d为间隙的厚度。
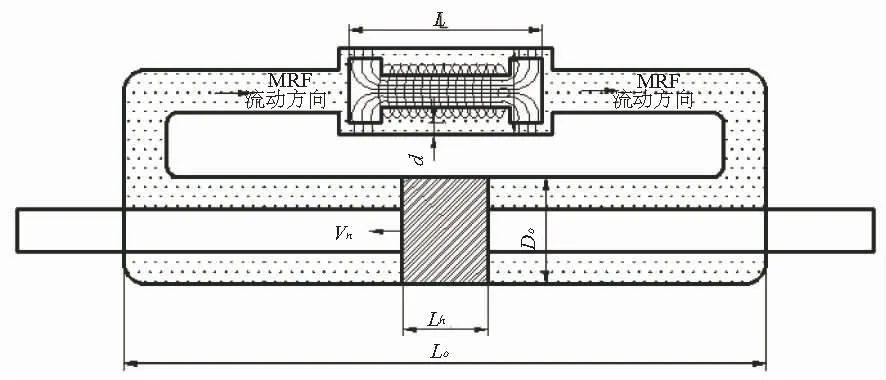
图1 MRFD的结构简图
2 旁通缸阻尼力
Bingham模型并没有反映出,当磁流变液在高剪切速率下出现剪切稀化的现象,而Herschel-Bulkley模型修正了此模型,考虑了流变过程中的剪切稀化的现象[17]。间隙处的速度分布如图2所示,其剪切应力τ和剪切应变率dv/dy的关系式是:
(1)
式中:τy(H)是在不同磁场强度下的剪切屈服应力;K是磁流变液的粘度;n是磁流变液的表现系数。
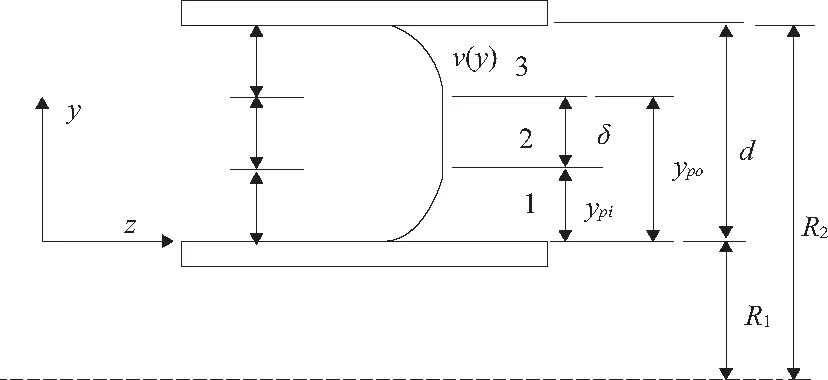
图2 Herschel-Bulkley模型间隙速度分布图
图2中v(y) 是不同y对应的速度;R1和R2分别是内杆直径和外筒内径;d,ypi和δ分别是间隙、屈服前区域1和屈服后区域2的厚度。间隙处速度的分布是对称的,则有:ypi=(d-δ)/2和ypo=(d+δ)/2。
文中,把磁流变液看成是不可压缩的。则根据Herschel-Bulkley模型,具有以下关系式:
(2)
其中,L是指阻尼区的长度。积分后,可以得到:τ(y)=(ΔP/L)y+C。利用边界条件:τ(ypi)=τy和τ(ypo)=-τy, 则屈服后区域厚度δ可以得到:δ=2Lτy/ΔP。
联合式(1)和式(2), 可以得到:
(3)
其中,A1和A2是常数。
对于屈服前区域1、3和屈服后区域2,有以下边界条件:
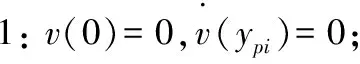
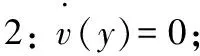
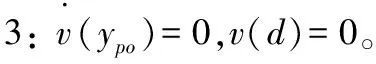
代入式(3)中,各个区域的流速:
(4)
(5)
(6)
则,每个区域的流量:
(7)
(8)
(9)
总流量为:
(10)
即:
(11)
流量和流速具有以下关系:
|Q|=A|v|
(12)
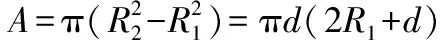

(13)
将δ=2L*τy/ΔP带入式 (13)中,有:
(14)
当n=1时,式(14)可以简化为Bingham模型:
ΔP(dΔP-2L*τy)2(dΔP+L*τy)=12KL*dΔP3|v|
(15)
(16)
式中第三项远小于前两项的和,则式(16)可以简化为:
(17)
根据基本的压力公式:
F=A·ΔP
(18)
对于间隙处,有A≈πd(R1+d),则有:
(19)
根据流量守恒Av=Ahvh,式(19)也可以写成以下形式:
(20)
其中,Ah=π(D02-Dr2) /4表示主缸处的横截面积,vh是活塞的速度。
3 旁通缸参数设计
旁通缸参数包括:长L,直径D,外筒厚度Δ,间隙厚度d,内杆两端直径R,内杆中部直径D1,内杆中部长度L1,和内杆两端长度L2,如图3所示。

图3 旁通缸阻尼区结构简图
3.1 间隙厚度
内杆和外筒采用高磁导率的材料,并忽略漏磁影响。间隙处的磁场强度远远大于其它区域的磁场强度。根据Kirchhoff定律:
NI=∑Hili
(21)
则有:
NI≈2Hd
(22)
说明间隙厚度越小,磁场强度越大。通常,旁通缸的间隙厚度的范围是0.25~2mm,考虑到加工的难度,取d=1mm。L=2L2,A≈πd(R1+d),则式(20)可化为:
F=2.688×106×Ah|vh|L2+6π(R1+0.001)×L2τy(H)=L2×(2.4×107×KAh|vh|+6π(R1+0.001)×τy(H))
(23)
由于τy(H)是随旁通缸的尺寸和外加磁场变化的,而磁场强度是由外加电流决定的。所以,下面的工作就是探究旁通缸的其它尺寸、电流和线圈对阻尼力的影响。
3.2 线圈
本文选用Lord公司的MRF-132DG,采用烃基载液,可以工作在阀模式或剪切模式下,工作温度是-40 ℃~130 ℃,闪点高于150 ℃,则MRF-132DG可以基本满足设计的需要。通过改变所加磁场,间接控制MRF-132DG的屈服应力。其特性如图4所示。

图 4 屈服应力磁场强度的关系曲线
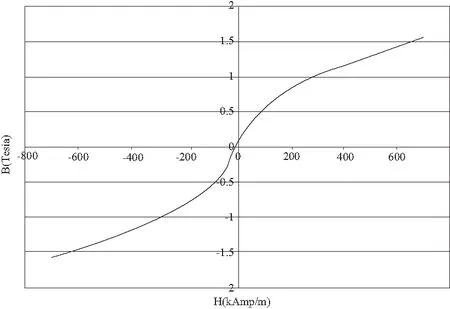
图5 磁感应强度与磁场强度的关系曲线
对图4采用5阶近似,得到拟合曲线关系式:
(24)
同样,对图5的第一象限的曲线拟合得到关系式:
H=288.1×B2+3.654×B+8.277
(25)
对式(23)和式(24)进行数字拟合,得到磁感应强度和屈服应力的关系曲线,如图6所示。
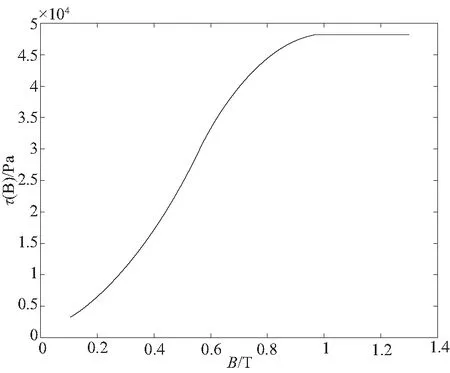
图6 屈服应力随磁感应强度B的变化曲线
通过改变线圈的电流的大小,可以改变阻尼区的磁感应强度,如果知道电流与磁感应强度的关系式,则磁流变液的屈服应力就可以算得。如图4所示,当磁场强度≥286 kA/m时,屈服应力达到最大。根据公式NI≈2Hd,则设计中的最大NI应≥572A。如果最大电流I已知,则线圈的圈数就可以求得。
3.3 内杆尺寸
由图7所知,内杆中部的磁感应强度通常远小于两端的磁感应强度,则可以忽略中部产生的阻尼力。仿真发现,当NI一定时,内杆中部的尺寸长度对磁感应强度影响不大。因此,内杆中部的尺寸主要取决于使用何种线圈。
为了探究内杆尺寸对阻尼力的影响,经试验分析,暂令NI=800 A,L1=60 mm,L2=10 mm,Δ=4 mm,D=50 mm,D1=20 mm,通过ANSYS仿真,可以得到不同内杆两端直径时,对应的磁感应强度分布图,图7是当R=32 mm时的仿真结果。取其平均磁感应强度,通过式(24)和式(25)来求得对应的屈服应力。

图7 R=32 mm时,磁感应强度分布的仿真结果
当活塞速度确定时,间隙处的流速会随内杆两端直径的变化而变化,不能达到控制变量的目的,则我们可以采用式(20)求阻尼力。这里令主缸尺寸:D0=100mm,Dr=40mm。将其带入式中,结果如图7所示。
由图8、图9可知,一定范围内,磁感应强度和阻尼力都随R的增大而增大。考虑到R增大带来的额外质量,取R=44mm。
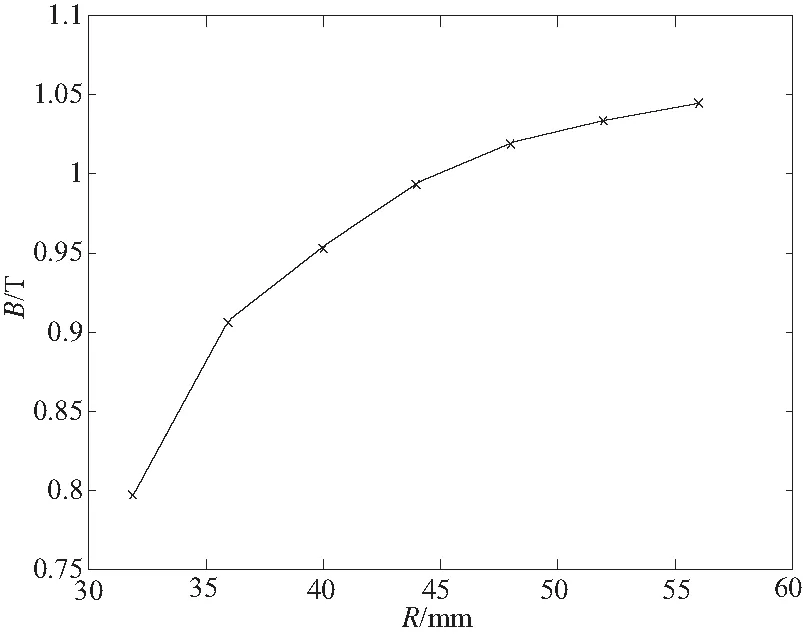
图8 R变化对磁感应强度的影响
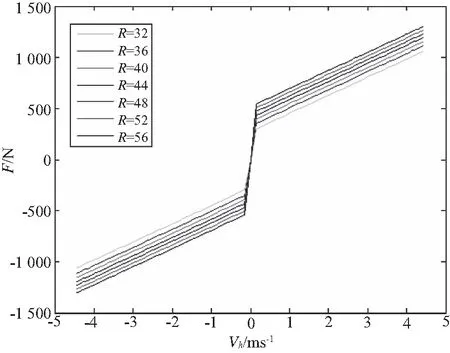
图9 R变化对阻尼力的影响
3.4 内杆两端长度L2
为探究L2的变化对磁感应强度的影响,令NI=480 A,以减小电流过大使得磁感应饱和带来的影响。经试验分析,取L1=60mm,R=44mm,Δ=4mm,D=50mm和D1=20mm,研究L2的变化对磁感应强度和阻尼力的影响,结果如图10、图11所示。
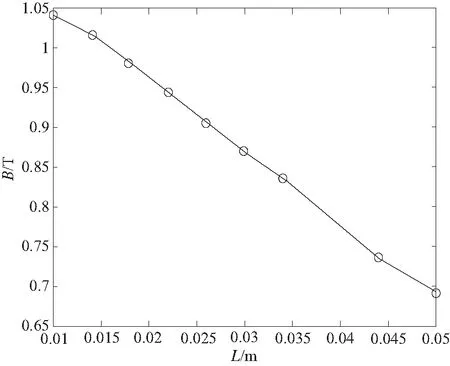
图10 L2变化对磁感应强度的影响
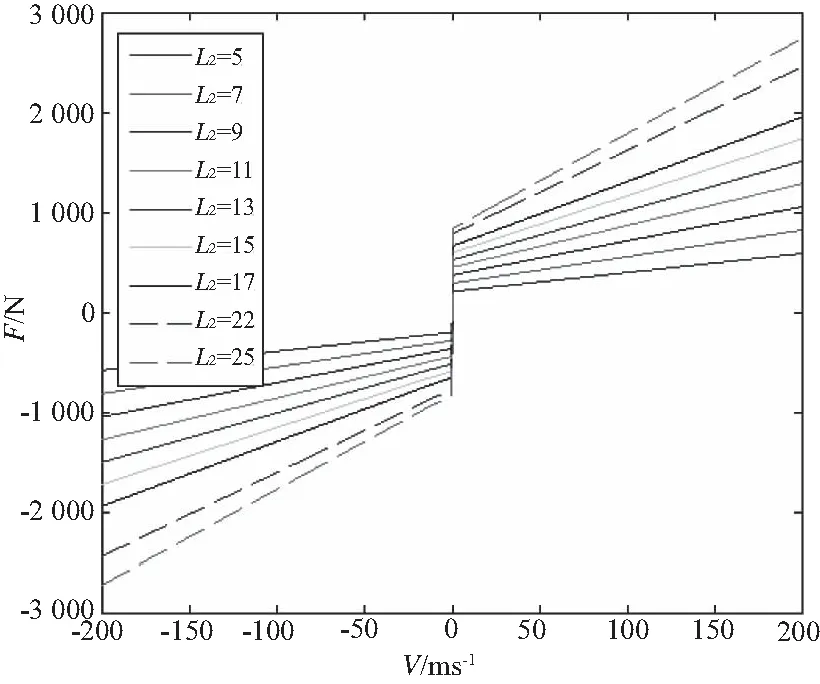
图11 L2变化对阻尼力的影响
由图10、图11可知,在一定范围内,磁感应强度随L2的增大而减小,阻尼力随L2的增大而增大。这里取L2=20mm。
3.5 外筒厚度Δ
令NI=480A,L1=60mm,L2=20mm,D=50mm。根据一般设计准则:Δ/(R+2d)∈(0.08,0.3), 则Δ∈(3.68,13.8)mm。仿真结果如图12、图13所示。

图12 Δ变化对磁感应强度的影响
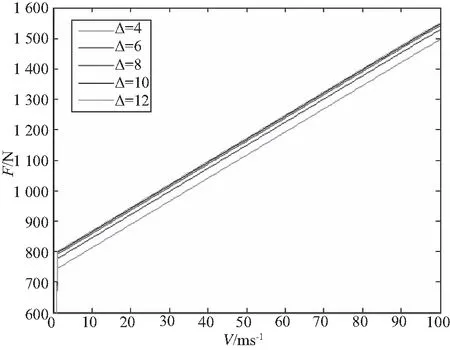
图13 Δ变化对阻尼力的影响
由图12、图13可知,在一定范围内,随着Δ的增大,B逐渐变大,并趋于稳定,阻尼力受厚度变化的影响几乎不大。取Δ=6mm,则缓冲器旁通缸的尺寸如表2所示。

表2 两种不同硬质合金的物理参数及用途
3.6 电流对阻尼力的影响
根据以上尺寸,建立缓冲器模型。若最大电流Imax=
1A,取N=1 600,则当I=0.5时,NI=800 。研究磁感应强度和阻尼力随电流大小变化的关系,结果如图14、图15所示。
对图14的磁感应强度和电流的关系曲线采用4阶拟合,得到:
B=-0.217 9×I4+1.004×I3-1.889×I2+2.392×I
(26)
联合式(24)、式(25)和式(26),屈服应力和电流的关系τy(I)就可以得到。也就是说,可以通过控制电流的变化来改变磁流变液的屈服应力,也就可以间接地控制缓冲器阻尼力的大小。
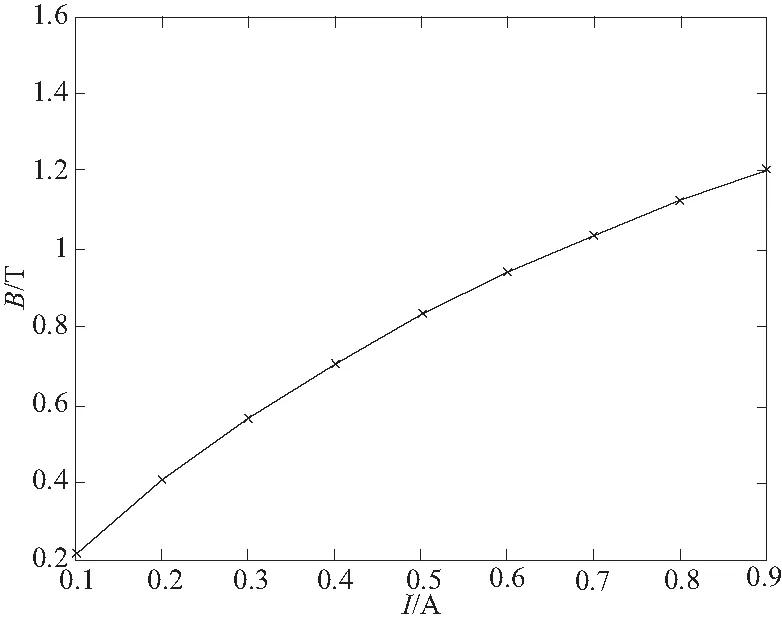
图14 电流变化对磁感应强度的影响
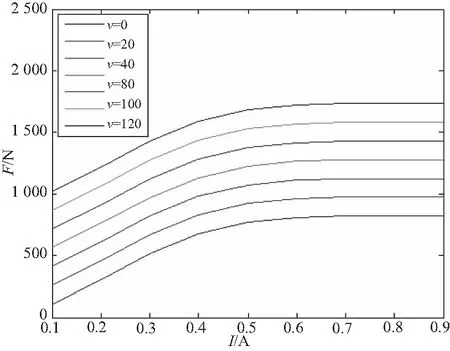
图15 不同流速下电流变化对阻尼力的影响
4 结语
推导了旁通剪切阀式磁流变液缓冲器的阻尼力算式,并提出了其用于月球着陆器缓冲器中的设计方法。通过仿真分析旁通缸各尺寸对阻尼力的影响,得出以下结论:
1) 当增大旁通缸的各个尺寸时,阻尼力具有持续增大的趋势。阻尼力的增速正比于内杆两端直径R和内杆两端长度L2的增速,为获得较大的阻尼力,可适当增大R和L2;
2) 在制造工艺允许的情况下,间隙厚度d越小越好;
3) 旁通缸外筒的厚度Δ对阻尼力的影响不大,则外筒的承受能力是需要首先考虑的要素。
此外,当电流大小一定时,阻尼力会随流速的增大而增大;当流速一定时,阻尼力会随电流的增大先增大后逐渐趋于稳定。
近年来,人们已经在磁流变液的研究上取得了许多重要成果,一些实验显示磁流变液在温度-60℃以下时仍表现出一定的流动性。月球上的环境十分恶劣,若要将其完美地应用到月球着陆器的设计中,研究具有良好的高低温特性的载液将是一个重要的发展方向。
[1] Yang. G. Large-scale magnetorheological fluid damper for vibration mitigation: modeling, testing and control[J]. Dissertation Abstracts International, 2001,6:46-74.
[2] Carlson J.D.Magnetorheological brake with integrated flywheel[P]. US Patent (2001): 6,186,290B1.
[3] Kavlicoglu B M, Gordaninejad F, Evrensel C A, et al. High-torque magnetorheological fluid clutch[J]. Proceedings of SPIE - The International Society for Optical Engineering, 2002, 4697:393-400.
[4] Carlson J.D., Catanzarite D.M., K.A. St. Clair. Commercial magneto-rheological fluid devices [J]. International Journal of Modern Physics B, 2012, 10(10):2857-2865.
[5] Ginder J M. Behavior of Magnetorheological Fluids [J]. Mrs Bulletin, 2013, 23(8):26-29.
[6] Ulicny J C, Mance A M. Evaluation of electroless nickel surface treatment for iron powder used in MR fluids[J] .Materials Science and Engineering, 2004, 369(1/2):309-313.
[7] Foister R T. Magnetorheological fluids [P]. US Patent: 5667715,1997.
[8] Gopal Swamy S. Magneto-rheological transmission clutch [P]. US Patent: 5896965,l999.
[9] Genç S, Phulé P P. Rheological properties of magnetorheological fluids [J]. Smart Materials & Structures, 2002, 11(1):140-146.
[10] Ciocanel C, Lipscomb G, Naganathan N G. A Constitutive Equation for Magnetorheological Fluid Characterization [J]. Journal of Phase Equilibria & Diffusion, 2008, 29(4):305-311.
[11] Kikuchi T, Oda K, Yamaguchi S, Furusho J. Leg-Robot with MR Clutch to Realize Virtual Spastic Movements[J]. Journal of Intelligent Material Systems and Structures, 2010, 21 (15): 1523-1529.
[12] Woo D, Choi S B, Choi Y T, et al. Frontal Crash Mitigation Using MR Impact Damper for Controllable Bumper [J]. Journal of Intelligent Material Systems and Structures, 2007, 18 (12): 1211-1215.
[13] 禹见达,陈政清,王修勇,等. 磁流变阻尼器与拉索振动控制研究[J]. 功能材料,2006(5):823-826.
[14] 李国发,韩明佐,单翠云,等. 磁流变力矩传动装置的有限元仿真及试验[J]. 吉林大学学报(工学版),2013,43(5):1284-1289.
[15] 唐龙,卢利平,岳恩,等. 磁流变液的研究与应用[J]. 重庆理工大学学报(自然科学版),2013(12):44-48.
[16] 李洪波. 磁流变缓冲阻尼器在月球着陆车软着陆过程中的理论与应用研究[D]. 西安:西北工业大学, 2002.

